یکی از مهمترین مهارت‌های لازم در زندگی هر انسانی داشتن تمرکز است. مهم نیست که کار شما چیست، اگر تمرکز نداشته باشید، انجام هر کاری مشکل می‌شود. در این میان، داشتن تمرکز برای کسانی که در حال تحصیل هستند (فرقی هم ندارد در چه رشته یا مقطعی) مهمتر است، زیرا ذهن آنها بطور مستمر در حال فعالیت است.

عدم انحراف از موضوع و داشتن تمرکز مهارتی است که برای کسب آن باید تلاش کرد. راه‌های مختلفی برای کسب این مهارت وجود دارد، که در میان آنها می‌توان به تفکر عمیق یا مِدی‌تیشن (meditation)، که از طریق ورزش‌هایی نظیر یوگا، و برخی از هنرهای رزمی حاصل می‌شود اشاره کرد. ولی روش‌های دیگری نیز برای اینکار وجود دارد که اساس آنها نرمش و تمرین با ذهن است، و چه نرمش و تمرینی بالاتر از محاسباتی که در ذهن صورت می‌گیرد.

این کتاب مهارت‌های لازم برای انجام محاسبات ذهنی را به شما آموزش می‌دهد. همانطور که در ادامه کتاب بیان می‌شود، هیچ فرمول معجزه‌آسایی برای انجام سریع محاسبات ذهنی وجود ندارد، و مانند هر کارِ مفیدِ دیگری، برای کسب آن به تمرین نیاز است. خیلی‌ها ممکن است بگویند ”ما می‌دانیم که برای انجام هر کاری نیاز به تمرین است، اگر می‌خواستیم تمرین کنیم، آن را در دوران مدرسه انجام می‌دادیم، و لازم نبود کسی آن را به ما گوشزد کند.“ ولی مسئله این است که برای انجام موثر هر کاری روش‌هایی وجود دارد، که ممکن است این روش‌ها کمتر شناخته شده باشند. اصولاً روش‌های انجامِ (سریع) محاسبات ذهنی با روش‌های انجام محاسبات با قلم و کاغذ با هم متفاوتند، و در بیشتر مدارس آنها را به دانش‌آموزان یاد نمی‌دهند. تفاوتی که این کتاب با یک کتاب عادی حساب دارد، یاد دادن روش‌های کارآمد برای انجام محاسبات ذهنی است. بخاطر داشته باشید که انجام سریع محاسباتِ ذهنی یک مهارت است که برای کسب آن باید تمرین کنید، تمرین‌هایی که ممکن است در ابتدا سخت و ملال آور باشند، ولی با انجام هر چه بیشتر آنها، به یک چیز عادی بدل خواهند شد. اگر خواهان کسب این مهارت هستید، باید تمرین کنید. اگر فقط به خواندن این کتاب اکتفا کنید، حالت کسی را خواهید داشت که یک کتاب آموزش سازِ موسیقی، یا یک کتاب نوت را خوانده و حالا انتظار دارد بتواند آن ساز را بنوازد. اینکار بدون انجام تمرین ممکن نیست، حتی برای نوابغ.

این کتاب مورد استفاده چه کسانی است؟

در یک کلام، همه! فرق نمی‌کند شما دانش‌آموز باشید، یا دانشجو، یا کارمند یا کاسب، یا حتی یک خانم خانه‌دار. انجام محاسبه و کسب تمرکز چیزی است که همه به آن نیاز دارند.

درباره نویسنده

ابهیشِک و.ر افپاد (Abhishek V.R) تحصیلاتش را در رشته مهندسی مکانیک در هند به پایان رساند و سپس برای ادامه تحصیل به انگلستان رفت و کارشناسی ارشد خودش را در رشته تحلیلِ تجارت از دانشگاه واریک دریافت کرد. او به برنامه نویسی، نوشتن و تدریس علاقه دارد.

بهار 1398، کامران بزرگزاد

مقدمه نویسنده

میخواهم این کتاب را با گفتن داستانی برای شما آغاز کنم که از گفتن آن کمی خجالت می‌کشم، با اینحال لازم آن را بشنوید زیرا برای شما روشن می‌کند که چگونه می‌توانید محاسبات ریاضی را در ذهن‌تان انجام دهید.

راستش را بخواهید من در کار با اعداد زیاد خوب نبودم، و مطمئناً باهوش هم نبودم. در واقع، من از ریاضیات متنفر بودم.

روزی در یک صبح زیبا، من بر ترکِ موتور پسرعمویم سوار بودم و از نسیم خنکی که به صورتم می‌خورد لذت می‌بردم.

تعطیلات تابستان به پایان ‌رسیده بود و پسرعمویم مرا به ایستگاه قطار رساند. من پس از لذت از بارانهای موسمی به خانه بازمی‌گشتم. همه چیز خوب بود تا اینکه زندگی چهره بدش را به من نشان داد.

آن روز در زندگی من حیاتی بود. تا نیم ساعت دیگر نتیجه امتحانات نهایی مشخص می‌شد. اهمیت این موضوع به این دلیل بود که مشخص می‌کرد آیا آنقدر رتبه دارم که وارد دانشگاه شوم یا نه.

وقتی به مدرسه می‌رفتم آنقدرها به نمرات خودم اهمیت نمی‌دادم. من تمام وقتم را یا به بازی‌های کامپیوتری تلف می‌کردم یا پای تلفن مشغول صحبت با دوست دخترم بودم.

هیچ هدف مشخصی نداشتم. اگر از من می‌پرسیدید در آینده می‌خواهم چه‌کاره شوم، جواب من این بود که ”تصمیمی نگرفتم، هنوز دارم بِش فکر می‌کنم“. من یک دانش آموز متوسط بودم که زندگی خودم را می‌گذراندم.

از اینکه بی دردسر زندگیم را سپری می‌کردم خوشحال بودم و فکر می‌کردم که می‌توانم بدون هیچ تلاشی وارد دانشگاه شوم. ولی قرار بر این بود که از این خواب بیدار شوم.

من و پسر عمویم به ایستگاه قطار رسیدیم، و منتظر قطار شدیم. در آن روزها او از معدود کسانی بود که گوشی هوشمند داشت. پسر عمویم پیشنهاد کرد که با گوشی او نتیجه امتحانات را ببینیم. او مشخصات مرا وارد کرد و ما منتظر نمایش نتیجه شدیم. لحظه‌ها مانند قرن طول می‌کشید. چهره هیجان‌زده او جایش را به دلسوزی داد.

نگاهی که در چهره‌ او بود فقط گویای آن بود که من حداقل نمرات لازم را برای ورود به دانشگاه کسب نکرده‌ام. گوشی را از او گرفتم و به نمرات خودم نگاه کردم. درجا خشکم زد.

بدترین نمرات ممکن را در ریاضی گرفته بودم و تنها با یک معجزه می‌توانستم وارد دانشگاه شوم.

بعداً فهمیدم که دوستانم نمرات بسیار بهتری گرفته‌اند. نمرات دوست دخترم آنقدر خوب بود که تصمیم گرفت پزشکی بخواند. او خیلی زود با من بهم زد. درست در جلوی چشمانم، بنظر می‌رسید که همه از من باهوش‌ترند.

از خودم بیزار شدم. اعتماد بنفسم را از دست دادم. نیازی نیست که بگویم این یکی از بدترین مراحل زندگی من بود. به بن‌بست خورده بودم، و نمی‌دانستم که آیا آینده‌ای دارم یا نه. چند ماه آتی را در افسردگی بسر می‌بردم و به چیزهایی فکر می‌کردم که موجب ناکامی من شده بودند.

پدر و مادرم نگران بودند. ولی خبرها پخش شد و یکی از دوستان پدرم پیشنهاد کرد تا به من توصیه‌نامه‌ای بدهد. زندگی فرصت دوباره‌ای به من داده بود، و بالاخره توانستم به طریقی وارد دانشگاه شوم.

ولی این کافی نبود تا اعتماد بنفس از دست رفته خودم را بدست آورم. هر کسی را که می‌شناختم نمراتش از من بهتر بود. در ذهن جوانِ من، نمره معیار هوش بود. و بر اساس این معیار، من کسی بودم که یکی از پایینترین ضرایب هوشی (IQ) جهان را داشت.

روزی یکی از روئسای جمهور فقید کشورم گفته بود ”رویاهای شما آن چیزهایی نیستند که در خواب می‌بینید، رویاهای واقعی آنهایی هستند که نمی‌گذارند شما بخواب روید.“

یکی از دغدغه‌های اصلی من که نمی‌گذاشت بخوابم، تبدیل شدن به یک انسان باهوش بود. من باید خیلی باهوش می‌شدم تا اعتماد از دست رفته خودم را بدست می‌آوردم. این باعث شد تا بخواهم هر آنچه را که ممکن است یاد بگیرم، و تصمیم گرفتم این سفر را از جایی شروع کنم که بیشتر از هر چیزی از آن متنفر بودم، یعنی ریاضیات، شروع کنم.

برایم بسیار معقول بود که از آنجا شروع کنم، زیرا همین بود که برایم بسیار گران تمام شده بود. بنابراین اولین کاری که کردم این بود که یاد بگیرم چگونه محاسبات را در ذهنم انجام دهم.

من همه کتابهایی که به اینکار ربط داشت را خواندم. همه مقالات و فیلم‌هایی که در اینمورد منتشر شده بود را دنبال کرده و غرق در مطالعه آنها شدم. همه چیزهایی را که از جاهای مختلف یادگرفته بودم را با هم ترکیب کردم تا سیستم منحصر بفرد خودم را بسازم، سیستمی که هر کسی می‌توانست از آن استفاده کند تا محاسبات ریاضی را بصورت ذهنی سریع و آسان انجام دهد.

اینها تکنیک‌هایی هستند که می‌توان آنها را ظرف چند دقیقه فراگرفت، و هنگامی که آنها را کشف کردم، مسیر فکری من بکلی عوض شد.

بدلیل اینکه محاسبات در ذهنم انجام می‌شد، حافظه من نیز بهتر شد. تمرکزم و بطور کلی، توانایی فکر کردنم بهبود یافت. ولی مهمتر از همه، یادگیری انجام محاسبات ذهنی محدودیت‌‌های ممکن را برایم کنار زد.

اگر حالا بعد از این همه تنفری که در بیشتر عمرم از ریاضیات داشتم می‌توانستم محاسبات را خیلی سریع در ذهنم انجام دهم، پس می‌توانم هر کاری دیگری را هم انجام دهم.

از آن موقع به بعد، من به هر نحوی که بود کلیه محدودیت‌هایی یادگیری خودم را کنار زدم. حالا مدرک کارشناسی ارشد خودم را گرفته‌ام و در حوزه تحلیل داده‌ها (data analytics) مشغول بکار هستم.

چیزی که بیش از همه از آن لذت می‌برم ریاضی است. به هر کسی که می‌گویم در مدرسه یک دانش‌آموز متوسط بوده‌ام کسی باور نمی‌کند. آنها تصور می‌کنند که من بطور مادرزاد یک نابغه بوده‌ام.

بخاطر داشته باشید که وقتی صحبت بر سر اعداد باشد، مغز من هیچ تفاوتی با مغز شما ندارد. من فقط کسی هستم که بطور اتفاقی سیستمی را ابداع کرده که می‌تواند محاسبات ذهنی را راحتتر انجام دهد.

این سیستم به مردم اجازه می‌دهد یک زندگی را تجربه کنند که اعداد و ریاضیات در آن مفیدترند.

این همان سیستمی است که با همه تنفری که نسبت به ریاضیات داشتم حالا به من اجازه می‌دهد محاسبات را در ذهن خودم سریعتر از یک ماشین حساب انجام دهم.

و حالا من قصد دارم راز محاسبات ذهنی را در این کتاب با شما در میان بگذارم. رازی که زندگی شما را تغییر خواد داد، همانطور که برای من چنین بود.

1

سیستم محاسبات ذهنی اُفپاد چیست؟

سیستم محاسبات ذهنی افپاد (Ofpad) تنها سیستمی است که به شما اجازه می‌دهد محاسبات را طوری در ذهن خودتان انجام دهید که از یک ماشین حساب معمولی نیز سریعتر باشد و این توانایی بی‌نظیری را در اختیار شما خواهد گذاشت. حتی اگر ریاضیات شما ضعیف است و از آن متنفرید، این تکنیک‌ها، که اساساً ساده هستند، برای همه جواب می‌دهند.

پس از مطالعاتی که بر روی بیش از 27 نفر از نوابغِ محاسبات ذهنی جهان انجام دادم و تکنیک‌های آنها را تحلیل کردم، تصمیم به نوشتن این کتاب گرفتم. من الگوهای پنهان (و برخی اوقات ’عجیبی‘) را که در تاکتیک‌های آنها برای انجام محاسبات وجود دارد را کشف کردم. و حالا، از امروز به بعد، راز موفقیت آنها می‌تواند راز موفقیت شما نیز باشد.

چیز قابل توجهی که در مورد این سیستم وجود دارد این است که آنقدر ساده است که حتی یک بچه هم می‌تواند آن را انجام دهد. حالا شما می‌توانید از راه‌برد‌های این نوابغِ ریاضی تقلید کنید، و در زندگی خودتان از قدرت محاسبه بهره ببرید. حافظه شما تقویت خواهد شد، و تمرکز بهتری را خواهید داشت، و قادر خواهید بود محاسباتی را انجام دهید که حتی قبلاً تصورش را هم نمی‌کردید.

در این کتاب شما قواعد پیچیده‌ای را یاد نخواهید گرفت که فقط برای مواقع خاصی جواب می‌دهند. در عوض، شما مفاهیم گسترده‌ای را یاد خواهید گرفت که می‌توانید در کلیه مسائل ریاضی آنها را بکار بگیرید.

شما قواعدی را یاد نمی‌گیرید که برای کاربرد آنها به کاغذ و قلم نیاز باشد. بعد از اتمام این کتاب شما خیلی سریعتر از قبل شروع به انجام محاسبات در ذهنتان خواهید کرد.

ولی بمنظور اینکه این تکنیک‌ها برای شما عادی شوند، باید تمرین‌هایی که در این کتاب آمده را انجام دهید.

حالا، پیش از اینکه جلوتر برویم باید با شما کاملاً روراست باشم. اگر چیزی که شما می‌خواهید این است که یک ” قرص جادویی“ داشته باشید که آن را قورت داده و نگهان به یک نابغه بدل شوید (چیزی که خودتان هم می‌دانید در عمل ممکن نیست)، بهتر است از مطالعه این کتاب صرفنظر کنید.

سیستم محاسبات ذهنی افپاد یک سرزمین خیالی بیهوده نیست. این چیزی است واقعی و تنها برای کسانی مانند شما جواب می‌دهد که حقیقتاً جدی هستند و قصد دارند هوش خودشان را تقویت کنند، و می‌خواهند برای اینکار وقت بگذارند و این مهارت جدید را کسب کنند.

هرچند انجام محاسبات در ذهن کار آسانی نیست (هیچ چیز باارزشی آسان نیست)، ولی من در این کتاب تا آنجا که امکان داشته محاسبات ذهنی را آسانتر کرده‌ام.

بنابراین اگر شما هم مانند اکثر خوانندگان این کتاب می‌خواهید تمام اسرار واقعی انجام محاسبات ذهنی را فرا بگیرید، طوری که از یک ماشین حساب معمولی هم سریعتر حساب کنید، و همینطور بر قدرت تمرکز و حافظه خودتان اضافه کنید، پس سیستم افپاد یکی از گزینه‌هایی نیست که اینکارها را برای شما انجام دهد، بلکه تنها گزینه‌ای است که می‌تواند این توانایی‌ها را در اختیار شما قرار دهد.

ممکن است فکر کنید که شما قبلاً این تکنیکها را دیده‌اید. ولی باور کنید هرگز چنین چیزهایی را قبلاً ندیده‌اید. این سیستم بکلی با بقیه متفاوت است، و چیزی نیست که آن را در مدرسه به شما آموزش داده باشند. روش‌هایی که من آنها را با شما درمیان خواهم گذاشت شما را تکان خواهند داد، و آن موقع بفکر خواهید افتاد که چرا قبلاً هیچ‌کس این روش‌ها را در مدرسه به شما یاد نداده بود.

2

استفاده از روش مجموع ارقام برای بررسی درستی محاسبات

در این فصل ما روش مجموع ارقام را توضیح خواهیم داد که با استفاده از آن می‌توانید درستی محاسباتِ ذهنی خود را بررسی کنید.

این روش چندین قرن است که برای ریاضیدانان شناخته شده است. ولی در مدارس زیاد آن را به دانش آموزان یاد نمی‌دهند، بنابراین بطور گسترده نیز مورد استفاده قرار نمی‌گیرد. با استفاده از این روش شما خیلی سریع می‌توانید درستی جمع، تفریق، ضرب و تقسیمی که انجام داده‌اید را بررسی کنید. ما ابتدا این روش را توضیح می‌دهیم تا شما بتوانید در سراسر این کتاب از آن استفاده کنید.

قواعد محاسبه مجموع ارقام

قاعده 1- مجموع ارقام چیزی نیست جزء جمع کلیه ارقام یک عدد. برای مثال، مجموع ارقام عدد 213 برابر 6 است. شما بسادگی می‌توانید این عدد را با جمع اعداد 2+1+3 حاصل کنید.

عدد: 213

مجموع ارقام: 2+1+3=6

قاعد 2- مجموع ارقام یک عدد همیشه باید یک عدد تک رقمی باشد. برای مثال، مجموع ارقام عدد 2134 برابر 1 است. شما این عدد را با جمع تک تک اعداد حاصل می‌کنید (2+1+3+4) که می‌شود 10. بدلیل اینکه مجموع ارقام باید یک عدد تک رقمی باشد، ما ارقام 10 را با یکدیگر جمع می‌کنیم تا عدد 1 را حاصل کنیم، پس مجموع ارقام 2134 برابر 1 است.

عدد 2134:

مجموع ارقام: 2+1+3+4=10

تقلیل به یک رقمی: 1+0=1

قاعد 3- وقتی ارقام را با هم جمع می‌کنید، باید 9 را نادیده بگیرید. مثلا! عدد 909 را در نظر بگیرید:

عدد: 909

مجموع ارقام: 0 (زیرا کلیه 9ها نادیده گرفته می‌شوند)

قاعده 4- شما می‌توانید اعدادی که مجموع آنها 9 می‌شوند را نیز نادیده بگیرید (مثل 1,8 یا 3,4 و 2). مثلاً در عدد 1802 اگر ما اعداد 1 و 8 را نادیده بگیریم، مجموع ارقام این عدد 2 خواهد بود.

عدد: 1802

مجموع ارقام: 0+0+2=2

بطور مشابه اگر 1 و 8 را نادیده نگیرید و آنها را در محاسبه وارد کنید مجموع آنها 11 می‌شود، و با تقلیل عدد 11 به یک عدد یک رقمی، باز هم مجموع ارقام عدد 1802 برابر 2 می‌شود.

عدد: 1802

مجموع ارقام: 1+8+0+2=11

تقلیل به یک عدد تک رقمی: 1+1=2

بنابراین شما چه ارقامی که مجموع آنها 9 می‌شود را بحساب آورید و چه نیاورید، در نتیجه محاسبه مجموع ارقام تفاوتی حاصل نمی‌شود. دلیل آن هم این است که بر طبق جدول زیر اعدادی که با 9 جمع می‌شوند، نهایتاً مجموع آنها خود این اعداد خواهد بود و جمع آنها با 9 تفاوتی در مجموع ارقام حاصل نمی‌کند:

1 + 9 = 10 = 1 + 0 = 1

2 + 9 = 11 = 1 + 1 = 2

3 + 9 = 12 = 1 + 2 = 3

4 + 9 = 13 = 1 + 3 = 4

5 + 9 = 14 = 1 + 4 = 5

6 + 9 = 15 = 1 + 5 = 6

7 + 9 = 16 = 1 + 6 = 7

8 + 9 = 17 = 1 + 7 = 8

9 + 9 = 18 = 1 + 8 = 9

به اعداد پررنگی که در سمت چپ قرار داردند و با 9 جمع شده‌اند توجه کنید. نتیجه این جمع‌ها بازهم خود این اعداد هستند. بنابراین با از قلم انداختن 9ها، یا اعدادی که مجموع آنها 9 می‌شود، شما کار محاسبه مجموع ارقام را ساده‌تر می‌کنید.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

3

مقدمه‌ای بر محاسبات ذهنی

این فصل مقدمه‌ای بر محاسبات ذهنی است و چگونگی ساختار بقیه کتاب و آنچه در فصل‌های آتی خواهد آمد را به شما نشان می‌دهد.

ما در اینجا تکنیک‌های عمومی جمع، تفریق، ضرب، و تقسیم را معرفی می‌کنیم. ولی چیزی که اول از همه در این فصل یاد خواهید گرفت، مهارتهای لازم برای محاسبات ذهنی است. شما اینکار را با یادگیری تکنیک ضرب اعداد در 11 شروع می‌کنید. تکنیک‌های کلی برای ضرب اعداد دیگر در فصل‌های آتی خواهند آمد.

ساختار درس

فصل‌های این کتاب ساختار زیر را خواهد داشت:

بخش 1: ابتدا مراحل تکنیک محاسبه ذهنی توضیح داده می‌شوند.

بخش 2: سپس ما برای روشنتر شدن مطلب این تکنیک‌ها را بر روی 3 مثال مختلف بکار خواهیم گرفت. هر یک از این مثال‌ها با قبلی متفاوت هستند و جنبه دیگری را در بر خواهند داشت.

بخش 3: بعد از ذکر مثال‌هایی که روش‌های محاسبه ذهنی را به شما نشان می‌دهند، به شما تمرین‌هایی داده می‌شوند تا بتوانید خودتان این تکنیکها را بر روی آنها اعمال کرده و به آنها مسلط شوید.

تعریف مضروب و ضریب

پیش از اینکه به تکنیک‌های محاسبه ذهنی بپردازیم، بیایید خیلی سریع منظور خودمان از مضروب (multiplicand) و ضریب (multiplier) را روشن کنیم. به مثال زیر توجه کنید:

43×23

در اینجا 43 مضروب نامیده می‌شود. این عددی است که در آن ضرب می‌کنیم. عدد 23 نیز ضریب نامیده می‌شود. این عددی است که عدد نخست در آن ضرب می‌شود.

مراحل مختلف تکنیک‌های محاسبه ذهنی به اعدادی که در یک عمل ضرب دخیل هستند بعنوان مضروب و ضریب اشاره می‌کند. بنابراین وقتی شما بدانید که منظور از مضروب و ضریب چیست، توضیحات داده شده را بهتر درک خواهید کرد. اگر اینها را فعلاً حفظ نکرده‌اید نگران نباشید، زیرا با مثال‌هایی که در اینجا خواهند آمد، هرگونه ابهامی دراین‌مورد برای شما رفع خواهد شد.

تکنیک ضرب اعداد در 11

بعنوان مقدمه‌ای بر محاسبات ذهنی، بیایید نگاهی به تکنیکی بیاندازیم که از آن برای ضرب اعداد در 11 استفاده می‌شود.

سه مرحله برای ضرب یک عدد در 11 وجود دارد:

مرحله 1: اولین رقم مضروب (یعنی عددی که در 11 ضرب می‌شود) بعنوان اولین رقم جواب کنار گذاشته می‌شود (از سمت چپ).

مرحله 2: برای بدست آوردن ارقام بعدی جواب، هر یک از ارقام بعدی مضروب با رقم سمت چپ خودش جمع می‌شود.

مرحله 3: آخرین رقم مضروب ، آخرین رقم جواب خواهد بود.

برای روشنتر شدن این تکنیک به مثال زیر توجه کنید.

مثال 1: بیایید ضرب زیر را انجام دهیم:

423×

11 _

مرحله 1: اولین رقم مضروب (یعنی عددی که در 11 ضرب می‌شود) بعنوان اولین رقم (از چپ) جواب نوشته می‌شود:

423×

11 _

4 ---

بنابراین ما 4 را بعنوان اولین رقم جواب می‌نویسیم.

مرحله 2: برای بدست آوردن ارقام بعدی جواب، هر یک از ارقام بعدی مضروب با عدد سمت چپ خودش جمع می‌شود. بنابراین، 4+2 می‌شود 6، و 6 رقم بعدی جواب ما خواهد بود.

423×

11_

46--

حالا نوبت اعداد 2 و 3 است که با هم جمع شوند و رقم بعدی را تشکیل دهند، پس 5 رقم بعدی جواب ما را تشکیل می‌دهد.

423×

11_

465-

مرحله 3: آخرین رقم مضروب، آخرین رقم جواب را تشکیل می‌دهد. بنابراین ما 3 را بعنوان آخرین رقم جواب می‌نویسیم.

423×

11 _

4653

بنابراین جواب 4653 است.

مثال 2: بیایید ضرب زیر را انجام دهیم:

534×

11 _

----

مرحله 1: اولین رقم مضروب (یعنی عددی که در 11 ضرب می‌شود) بعنوان اولین رقم جواب نوشته می‌شود (از چپ):

534×

11 _

5---

بنابراین ما 5 را بعنوان اولین رقم جواب می‌نویسیم.

مرحله 2: برای بدست آوردن ارقام بعدی جواب، هر یک از ارقام بعدی مضروب با عدد سمت چپ خودش جمع می‌شود. بنابراین، 5+3 می‌شود 8، و 8 رقم بعدی جواب ما خواهد بود.

534×

11_

58--

حالا نوبت اعداد 3 و 4 است که با هم جمع شوند و رقم بعدی را تشکیل دهند، پس 7 رقم بعدی جواب ما را تشکیل می‌دهد.

534×

11 _

587-

مرحله 3: آخرین رقم مضروب، آخرین رقم جواب را تشکیل می‌دهد. بنابراین ما 4 را بعنوان آخرین رقم جواب می‌نویسیم.

534×

11_

5874

بنابراین جواب5874 است.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

4

روش ناکارآمد برای انجام محاسبه

تکنیکی که در فصل قبل آن را یادگرفتید برای ضرب اعدد در 11 بود، ولی در مورد اعداد بزرگتر چه باید کرد؟ این موضوعی است که ما آن را در فصل‌های آتی مورد بررسی قرار می‌دهیم. نیازی نیست تا شما برای هر عدد قاعده خاصی را حفظ کنید. چند تکنیک عمومی هست که می‌توانید از آنها در مورد هر عددی استفاده کنید.

پیش از اینکه به این تکنیک‌های عمومی بپردازیم، باید به شما درمورد مشکل واقعی که در پیش است بگویم. این به اشتباهی مربوط است که شما همیشه مرتکب می‌شده‌اید و باعث کندی محاسبات ذهنی شما می‌شده، و تقصیر هم از شما نبوده، زیرا این چیزی است که در بیشتر مدارس آن را به دانش‌آموزان یاد می‌دهند.

بسیاری از مردم تصور می‌کنند که برای حساب کردن به ماشین حساب، یا حداقل به یک قلم و کاغذ، نیاز دارند. مشکل واقعی در روش غیر کارآمدی است که در مدرسه به شما یاد داده‌اند. و این همان چیزی است که انجام محاسبات را برای شما سخت‌ کرده، چه رسد بخواهید آنها را در ذهن خودتان انجام دهید.

اشتباه رایجی که خیلی‌ها به آن باور دارند این است که شما برای خوب حساب کردن باید استعداد خاصی داشته باشید. ممکن است چنین چیزی را قبلاً شنیده باشید، یا خودتان به آن باور داشته باشید. ولی این اصلاً حقیقت ندارد.

اگر شما یکی از آن میلیون‌ها نفری هستید که به این دروغ باور ندارند، پس حالا باید با تصمیم بگیرید که با حقیقت روبرو شوید، زیرا اگر اینطور نباشد، حتی اگر خیلی هم باهوش باشید هرگز فواید محاسبه ذهنی و اعداد را در زندگی خودتان تجربه نخواهید کرد.

همانطور که گفتم، تقصیر از شما نیست زیرا این دروغی است که سیستم آموزشِ ریاضیِ کنونی آن را به شما تحمیل کرده. بنابراین اگر انجام محاسبات ذهنی برای شما مشکل است، خودتان را سرزنش نکنید، سیستمی را سرزنش کنید که به دانش‌آموزان روش‌های قدیمی حساب کردن را یاد می‌دهد. این سیستم طوری طراحی شده که فقط %1 از مردم آن را بخوبی انجام می‌دهند و بقیه ما آن را بسختی بکار می‌گیریم.

هنگامی که من در فصل بعد اسرار ساده محاسبات ذهنی را برای شما فاش کردم، شما از اینکه چرا قبلاً اینها را در مدرسه به شما یاد نداده‌اند شوکه خواهید شد. و هنگامی که آنها را یادگرفتید، حساب کردن برای شما فوراً به یک چیز مفید و لذت بخش بدل خواهد شد.

واقعیتی که باعث می‌شود ما در مدرسه کندتر حساب کنیم این است که بیش از حد بر روی استفاده از حافظه کاری (Working memory) تاکید می‌کند. حافظه کاری، حافظه کوتاه-مدتی است که شما نیاز دارید تا برای انجام یک کار از آن استفاده کرده و اطلاعات را مرتب کنید. این شبیه حافظه RAM در کامپیوتر شما است.

روشی که برای انجام محاسبات در مدرسه به ما یاد داده‌اند چنان ناکارآمد است که اگر سعی کنیم محاسبات را بصورت ذهنی انجام دهیم، بیشتر حافظه کاری ما را مصرف خواهد کرد. بنابراین مانند کامپیوتری که زیاد از حد از آن کار می‌کشیم (و باصطلاح هَنگ می‌کند)، مغز ما هم کُند کار خواهد کرد. این همان چیزی است که انجام محاسبات ذهنی را سخت می‌کند.

برای انجام سریع محاسبات در ذهن خودتان، باید خلاف آنچه در مدسه به شما یاد داده شده عمل کنید. و این دقیقاً همان کاری است که در چند دقیقه آینده انجام خواهید داد.

پیش از هر چیز، لازم است به شما نشان دهم که چرا باید از آنچه قبلاً در مدرسه انجام می‌داده‌اید پرهیز کنید. این ممکن است برای شما تعجب برانگیز باشد، زیرا خیلی‌ها تصور می‌کنند که تنها راه محاسبه همان است که در مدرسه به آنها یاد داده شده، ولی واقعیت این است که آنچه موجب کندی شما بوده استفاده از همین روش است. اجازه دهید با ارائه یک مثال منظور خودم را روشن‌ کنم. فرض کنید شما می‌خواهید عدد 73210 را در 3 ضرب کنید:

73201×

3 --------

شما کار خودتان را با ضرب یک و سه آغاز می‌کنید تا سه را حاصل کنید. سپس صفر و سه را درهم ضرب می‌کنید تا صفر را حاصل کنید، و کارتان را با ضرب اعداد دو و سه ادامه می‌دهید تا شش را بگیرید. سپس ما سه و سه را درهم ضرب می‌کنیم تا نه را حاصل کنیم، و نهایتاً ما هفت و سه را درهم ضرب می‌کنیم تا بیست و یک را حاصل کنیم.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

5

مقدمه‌ای بر روش از چپ به راست

راز انجام سریع محاسبات ذهنی خلاف آن چیزی است که در مدرسه یادگرفته‌اید. این روش، روش از چپ به راست نام دارد.

اجازه دهید تاکید کنم که اگر شما از این روش استفاده نکنید، هر ترفندی که در این کتاب برای انجام محاسبات ذهنی یاد می‌گیرید، بی‌فایده خواهد بود. چیزی که سرعت محاسبات ذهنی را تضمین می‌کند، استفاده از همین روش است. بقیه چیزها بر اساس این روش هستند. دلیل اینکه این تکنیکِ ساده خوب جواب می‌دهد این است که دست و پای شما را از حافظه کاری رها می‌کند.

رمز انجام محاسبات ذهنی این است که بجای انجام محاسبات از راست به چپ، آنها را از چپ به راست انجام دهید. به همین جهت است که می‌گوییم این روش مخالف روشی است که در مدرسه به شما آموزش داده شده. حالا بیایید سعی کنیم مثال قبلی خودمان، یعنی 72101×3، را با استفاده از این روش حل کنیم.

73201×

3 ------

پیش از اینکه ادامه این مطالب را بخوانید سعی کنید خودتان این ضرب را از چپ به راست انجام دهید. مطمئن هستم که خیلی سریع این کار را انجام خواهید داد:

با ضرب 7×3 شما 21 را حاصل می‌کنید:

73201×

3 21----

با ضرب 3×3 شما 9 را حاصل می‌کنید:

73201×

3 219---

با ضرب 2×3 شما 6 را حاصل می‌کنید:

73201×

3 2196--

با ضرب 0×3 شما 0 را حاصل می‌کنید:

73201×

3 21960-

با ضرب 1×3 شما 1 را حاصل می‌کنید:

73201×

3 219603

آیا متوجه شدید که حتی پیش از اینکه همه مسئله را بخوانید، پیشتر جواب آن را پیدا کردید؟ در اینجا نیازی ندارید تا چیزی را حفظ کنید تا بعداً آن را بخاطر آورید. بنابراین محاسبات شما خیلی سریعتر خواهند شد.

شما اینکار را برای ضریب یک‌رقمی 3 انجام دادید. حالا تصور کنید بتوانید همین کار را برای ضرایب بزرگتر دو یا سه رقمی انجام دهید، و تصور کنید جمع، تفریق و تقسیم را با همین سرعت انجام دهید.

اجازه دهید به شما این قول را بدهم که این کارها نیز به همان سادگی چیزی است که درمورد روش چپ به راست توضیح دادم، و من در دو فصل آتی جزئیات آنها را بیان خواهم کرد.

پیش از اینکه به این مطالب بپردازم، برای یک لحظه تصور کنید که فردا که بیدار می‌شوید قادر خواهید بود به سرعت برق محاسبات را در ذهنتان انجام دهید. خانواده و دوستان طوری به شما نگاه خواهند کرد که انگار شما یک جور نابغه هستید.

بدلیل اینکه محاسبات را در ذهنتان انجام می‌دهید، در طی این روند حافظه شما نیز تقویت می‌شود. همچنین، توانایی فکر کردن و تمرکز شما سریعاً بهبود خواهد یافت. پس نه تنها شبیه یک نابغه خواهید شد، بلکه حقیقتاً به یک نابغه بدل خواهید شد.

آیا می‌دانید قسمت خوب این قضیه در چیست؟ شما بلافاصله پس از اتمام این کتاب مانند یک نابغه فکر خواهید کرد. به نوبه خودش، این بر روی حوزه‌های دیگر زندگی شما نیز تاثیر مثبت خواهد گذاشت. من خیلی مشتاقم که چگونگی این کار را به شما نشان دهم.

6

جمع و تفریق

در این فصل ما چگونگی انجام جمع و تفریق با استفاده از روش چپ به راست را توضیح می‌دهیم. این تکنیک‌ها مشابه یکدیگرند، بنابراین ما آنها را در یک فصل بررسی می‌کنیم.

جمع از چپ به راست

ما در فصل قبل دیدیم که راز محاسبات ذهنی این است که محاسبه را بجای اینکه از راست به چپ انجام دهیم، آن را از چپ به راست انجام دهیم. هنگامی که شما محاسبات خود را به این شکل انجام می‌دهید، حتی قبل از اینکه همه محاسبه را تکمیل کنید، جواب آن برای شما ظاهر می‌شود.

اگر بخواهید با قلم و کاغذ کار کنید، انجام محاسبات از راست به چپ مناسب است. ولی وقتی شما محاسبه را به این روش، یعنی همان که در مدرسه به شما یاد داده‌اند انجام دهید، جواب را بصورت معکوس تولید می‌کنید، و همین است که انجام محاسبات را در ذهنتان مشکل می‌کند.

درابتدا روش چپ به راست غیرعادی بنظر می‌رسد، ولی شما بعداً خواهید دید که انجام محاسبه از چپ به راست طبیعی‌ترین روش انجام محاسبه در ذهن است. پس بیایید ابتدا این روش را برای جمع بکار بگیریم.

مثال 1: اعداد زیر را با هم جمع کنید:

5321+

1234

- - - -

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

7

ضرب از چپ به راست

در این فصل ما به چگونگی انجام عمل ضرب به روش از چپ به راست نگاهی خواهیم انداخت. در فصل قبل شما با قدرت این روش در انجام جمع و تفریق آشنا شدید. ما در این فصل برای ضرب از این روش استفاده می‌کنیم.

راز انجام سریع ضرب نیز در کاربرد روش از چپ به راست است. زیبایی این روش در این است که می‌توان آن را در مورد هر جفتی از اعداد بکار گرفت.

برای درک این فصل پیش‌نیازی وجود دارد و آنهم دانستن جدول ضرب است. معمولاً این جدول را در دبستان به دانش‌آموزان یاد می‌دهند. اگر شما این جدول را فراموش کرده‌اید، باید دوباره آن را حفظ کنید.

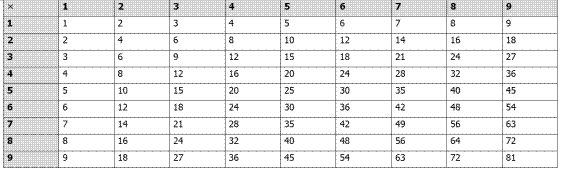
هنگامی که به مثال‌ها و تمرین‌های این فصل نگاه می‌کنید، باید یاد بگیرید که این اعداد را در ذهن خودتان مجسم کنید. اینجاست که تمرین اهمیت پیدا می‌کند. هر چه بیشتر تمرین کنید، حافظه شما نیز آماده‌تر می‌شود، و باعث می‌شود اعداد را راحت‌تر بخاطر بسپارید.

ضرب از چپ به راست وقتی ضریب یک رقمی باشد

ما کار خودمان را با ضرب اعداد در اعداد یک رقمی آغاز می‌کنیم.

مثال 1: بیایید عدد 5321 را در 4 ضرب کنیم:

5321 ×

- - - - -

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

8

اضطرابِ ریاضی

بعضی‌ها وقتی می‌خواهند چیزی را حساب کنند، دل‌شوره می‌گیرند، کف دستشان عرق می‌کند و تمرکز برای آنها مشکل می‌شود.

این پدیده اضطرابِ ریاضی (Mathematical anxiety) نامیده می‌شود، و بیشتر ما، به درجات مختلف، به آن مبتلا هستیم. ممکن است فکر کنید چون توانایی‌های ریاضی شما کم است دلشوره دارید. ولی اغلب چیز دیگری هم می‌تواند مطرح باشد، دلیل اینکه عملکرد شما در ریاضی ضعیف است این است که درمورد آن اضطراب دارید.

اضطراب ریاضی موجب کاهش حافظهِ کاری شما می‌شود. نگرانی در مورد حل یک مسئله ریاضی، حافظه کاری شما را مصرف کرده و مقدار اندکی از آن را باقی می‌گذارد تا با خود مسئله دست و پنجه نرم کنید.

بنابراین ما با ساده‌ترین مسائل ریاضی، که حتی از قبل راه حل آنها را می‌دانیم، مشکل خواهیم داشت. در اینصورت، هنگام روبرو شدن با یک مسئله ریاضی داشتن آرامش ضروری است. اسرار محاسبات ذهنی که ما در این کتاب آنها را به شما ارائه می‌دهیم بکلی باعث تغییر رویکرد شما در حل مسائل ریاضی می‌شود و محاسبات ذهنی را به راحتی خواندن یک مجله بدل می‌کند.

ولی تا وقتی شما آرامش نداشته باشید، این اسلحه جدیدِ ریاضی باعث نخواهد شد تا به یک ابر قهرمان بدل شوید. هر موقع با اضطراب ریاضی روبرو شدید، یک نفس عمیق بکشید و پس از آن قادر خواهید بود محاسبات را سریعتر انجام دهید. از دانش خود درباره طرز کار حافظه کاری خودتان استفاده کنید تا به خودتان تلقین کنید از ریاضیات لذت می‌برید. خواهید دید که هر مسئله ریاضی چالشی است که هوش شما را افزایش می‌دهد.

خواهید دید که نه تنها مسائل ریاضی را سریعتر حل می‌کنید، بلکه از حل آنها لذت می‌برید.

9

مجذور کردن

در این فصل ما به چگونگی مجذور کردن سریع اعداد می‌پردازیم. منظور از مجذور کردن یک عدد ضرب یک عدد در خودش است (مثلاً 5×5 یا 43×43). ما معمولاً مجذور یک عدد (که به آن مربع عدد نیز گفته می‌شود) را بصورت 5² یا 5^2 می‌نویسیم.

مجذور کردن اعدادی که به 5 ختم می‌شوند

ابتدا بیایید به چگونگی مجذور کردن اعدادی بپردازیم که به 5 ختم می‌شوند. ما بعداً به چگونگی مجذور کردن همه اعداد خواهیم پرداخت، و از همین اصول مجذور کردن اعداد منتهی به 5، برای آنها هم استفاده می‌کنیم.

مراحل مجذور کردن اعدادی که به 5 منتهی می‌شوند بصورت زیر است:

مرحله 1- اولین رقمِ عدد (از سمت چپ) را با 1 جمع کنید و آن را در رقمِ اول ضرب کنید.

مرحله 2- بدنبال حاصل ضرب مرحله 1، عدد 25 را قرار دهید تا مجذور مورد نظر حاصل شود.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

10

روش پُل برای ضرب

در این فصل ما به چگونگی استفاده از روش پُل (Bridge Method) برای ضرب سریع اعداد می‌پردازیم. شما با استفاده از این روش قادر خواهید بود اعداد دو و سه رقمی را در هم ضرب کنید.

مراحل مختلف استفاده از روش پُل به صورت زیر است:

مرحله 1- اولین رقم مضروب را در اولین رقم ضریب ضرب کرده و آن را بعنوان عدد سمت چپ جواب کنار بگذارید.

مرحله 2- جفت‌های بیرونی را درهم، و جفت‌های درونی را درهم ضرب کنید.

مرحله 3- حاصل جمع ضرب‌ِ جفت‌های بیرونی و درونی را بعنوان رقم بعدی جواب کنار بگذارید.

اگر ارقام دیگری باقیمانده باشد، مرحله 2 را برای آنها تکرار کنید.

مرحله 4- آخرین رقم مضروب (رقم سمت راستی) را در آخرین رقم ضریب ضرب کنید و آن را بعنوان رقم سمت راست جواب کنار بگذارید.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

11

روش مرد ویترویوسی

در این فصل روش مرد ویترویوسی (Vitruvian Man) را شرح می‌دهیم. نام این تکنیک به این دلیل مرد ویترویوسی است، زیرا تجسمِ این روش شبیه طرح مرد ویترویوسی اثر لئوناردو داوینچی است. مراحل مختلف شبیه روش پل هستند. تنها چیزی که در این روش متفاوت است، تجسم ذهنی آن است.

مثال 1: ضرب 32×13 را به روش مرد ویترویوسی انجام دهید

$Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\Mental Math\summary_files\image001.png$

بیایید از روش جدید برای تجسم این ضرب استفاده کنیم

مرحله 1- اولین رقم مضروب را در اولین رقم ضریب ضرب کرده و آن را بعنوان عدد سمت چپ جواب کنار بگذارید. بنابراین، 3 را در 1 ضرب می‌کنیم، که می‌شود 3

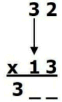
$Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\Mental Math\summary_files\image002.png$

مرحله 2- جفت‌های بیرونی را درهم، و جفت‌های درونی را درهم ضرب کنید.

بنابراین جفت 3 و 3 را در هم ضرب می‌کنیم که می‌شود 9، همچنین جفت 2 و 1 در هم ضرب می‌کنیم که می‌شود 2

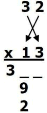
$Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\Mental Math\summary_files\image003.png$

مرحله 3- حاصل جمع ضرب‌ِ جفت‌های بیرونی و درونی را بعنوان رقم بعدی جواب کنار بگذارید.

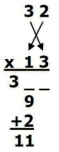
$Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\Mental Math\summary_files\image004.png$

با جمع دهگان 11 با 3، 3 به 4 تبدیل می‌شود

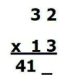
$Description: Description: Description: Description: Description: Description: C:\Users\kami\Documents\My Books\Mental Math\summary_files\image005.png$

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

12

روش یکان دهگان

روش یکان و دهگان روش دیگری برای ضرب است که با استفاده از آن می‌توانید سریعاً اعداد بزرگ را درهم ضرب کنید.

مفاهیم لازم برای روش یکان دهگان

پیش از اینکه به مراحل مختلف این روش بپردازیم، لازم است تا مفاهیمی که در رابطه با این روش وجود دارد را درک کنید:

1) یک رقم عبارت است از یک عدد تک رقمی (مثلاً 4، 2، و 0).

2) حاصل ضرب یک رقم در رقم دیگر، همیشه یا یک عدد تک رقمی دیگر خواهد بود یا یک عدد دو رقمی، ولی نه بزرگتر. حداکثر حالتی که در اینجا وجود دارد 9×9=81 است.

3) در برخی از مواقع که ضرب یک رقم در رقم دیگر یک عدد تک رقمی می‌شود، برای سادگی استفاده از روش یکان و دهگان، این عدد را با اضافه کردن 0 به سمت چپ آن، به یک عدد دو رقمی تبدیل می‌کنیم (مثلاً 2×3=06).

4) برای اعداد دو رقمی، رقم سمت چپ، رقم دهگان و رقم سمت راست، یکان را تشکیل می‌دهند (مثلاً در عدد 23 رقم دهگان 2 و رقم یکان 3 است).

5) ما در روش ضرب یکان دهگان یا از یکان استفاده می‌کنیم یا از دهگان، ولی هیچ وقت از هر دو آنها استفاده نمی‌کنیم.

برای روشن‌تر شدن موضوع بیایید به چند مثال توجه کنیم.

رقم یکان ضرب‌های زیر را بدست آورید. در اینجا سرعت بسیار مهم است، و شما باید بدون اینکه به دهگان فکر کنید، تنها یکان را درنظر بگیرید.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

13

تقسیم به روش پرچم و میله

در این فصل ما روش میله و پرچم را برای تقسم سریع توضیح می‌دهیم. برای استفاده از این روش، شاید لازم باشد در ابتدا اعداد را روی کاغذ بنویسید، ولی با تمرین‌های بیشتر شما قادر خواهید بود آن را بدون استفاده از قلم و کاغذ نیز انجام دهید.

روش پرچم و میله

پیش از کاربرد روش پرچم و میله (Flag & Pole) مهم است که بدانید کدامیک از ارقام پرچم، و کدامیک از آنها میله هستند.

الف) اولین عدد، یا اولین دسته ارقام میله را تشکیل می‌دهد.

ب) دومین عدد، یا دومین دسته ارقام پرچم را تشکیل می‌دهد.

بیایید چند عدد را در نظر بگیریم.

در عدد 25، 2 میله، و 5 پرچم است. ما می‌توانیم آن را بصورت 2⁵ بنویسیم.

توجه: در اینجا 2⁵ را نباید دو بتوان پنج بخوانید. این طرز نمایش هیچ ارتباطی با توان ندارد. علت اینکه این طرز نمایش میله و پرچم نام دارد این است که عدد پایینی مانند پایه، یا میله، و عدد بالایی شبیه پرچم است که در بالای میله قرار دارد!

در عدد 83، 8 میله، و 3 پرچم است. ما می‌توانیم آن را بصورت 8³ بنویسیم.

...........................................

برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.

14

حفظ مهارت‌های محاسبات ذهنی

در این فصل ما به چگونگی حفظ مهارت‌های محاسبات ذهنی می‌پردازیم. هر گونه مهارتی که شما یاد می‌گیرید، اگر بر روی آن تمرین نکنید، با مرور زمان از بین می‌رود. بنابراین برای حفظ مهارت فراگرفته شده انجام تمرین بسیار مهم است.

بیایید تفاوتی که میان دانش‌آموزانی که تمرین ندارد و دانش‌آموزانی که تمرین دارد را در نظر بگیریم.

دانش‌آموزانی که تمرین ندارد

1) آنها پس از پایان این کتاب دیگر هرگز تمرین نمی‌کند.

2) آنها تکنیک‌های این کتاب را بطور مبهم بخاطر می‌آوردند.

3) سرعت محاسبات ذهنی آنها همانقدر خواهد بود که پیش از شروع خواندن این کتاب داشتند.

دانش‌آموزانی که تمرین دارد

1) دانش آموزی که تمرین دارد، حداقل روزی 10 دقیقه تمرین می‌کند.

2) آنها بطور کامل تکنیک‌های توضیح داده شده در این کتاب را فراگرفته و آنها را همیشه بخاطر خواهند داشت.

3) آنها کاملاً با مهارت‌های محاسبات ذهنی خو می‌گیرند.

چالش‌هایی که برای تمرین در مقابل شما قرار دارند

هنگامی که می‌خواهید بطور مرتب تمرین کنید، با دو مشکل روبرو می‌شوید:

1. اول اینکه شما به مسائلی نیاز دارید که بر روی آنها تمرین کنید.

2. و دوم اینکه باید بخاطر داشته باشید تا بطور مرتب تمرین کنید.

برای هر دو این مشکلات راه‌حلی وجود دارد.

اگر شما در سایت ما به آدرس http://ofpad.com/mathworkbook ثبت‌نام کنید، ما به مدت 8 هفته بطور مرتب تمرین‌ها را به آدرس ایمیل شما می‌فرستیم.

Like: ,

ترجمه‌های کامران بزرگزاد

show_banner(0);

ترفندهای محاسبات ذهنی

نوشته ابهیشِک و.ر اُفپاد (Abhishek V.R Ofpad)

ترجمه کامران بزرگزاد ایمانی

Mental Math

مقدمه مترجم

درباره کتاب

این کتاب مورد استفاده چه کسانی است؟

درباره نویسنده

مقدمه نویسنده

1

سیستم محاسبات ذهنی اُفپاد چیست؟

2

استفاده از روش مجموع ارقام برای بررسی درستی محاسبات

قواعد محاسبه مجموع ارقام

عدد: 213

مجموع ارقام: 2+1+3=6

عدد 2134:

مجموع ارقام: 2+1+3+4=10

تقلیل به یک رقمی: 1+0=1

عدد: 909

مجموع ارقام: 0 (زیرا کلیه 9ها نادیده گرفته می‌شوند)

عدد: 1802

مجموع ارقام: 0+0+2=2

عدد: 1802

مجموع ارقام: 1+8+0+2=11

تقلیل به یک عدد تک رقمی: 1+1=2

3

مقدمه‌ای بر محاسبات ذهنی

ساختار درس

تعریف مضروب و ضریب

43×23

تکنیک ضرب اعداد در 11

423×

11 _

4 ---

423×

11_

46--

423×

11_

465-

423×

11 _

4653

534×

11 _

----

534×

11 _

5---

534×

11_

58--

534×

11 _

587-

534×

11_

5874

4

روش ناکارآمد برای انجام محاسبه

73201×

3

--------

5

مقدمه‌ای بر روش از چپ به راست

73201×

3

------

73201×

3

21----

73201×

3

219---

73201×

3

2196--