ترجمههای کامران بزرگزاد

آیا هیچچیز یک عدد شمرده میشود؟
متحد کردن نسبیت با نظریه
کوانتوم
محتملتر از آن است که فکر
میکنید
26!
= 403,291,461,126, 605,635,584,000,000
6,670,903,752,021,072,
936, 960
(عددی 17,525,170 رقمی) بزرگترین عدد اولی که تاکنون شناخته شده
عدد 42 اصلاً هم بیفایده نیست
اولین
کتابی که از یان استوارت (Ian Stewart) ترجمه کردم ”چرا
زیبایی واقعیت است؟“ بود و این دومی کتابی است که از این ریاضیدان انگلیسی به زبان
فارسی ترجمه میکنم. مانند دیگر کتابهای عمومی استوارت، او در این کتاب نیز تلاش
میکند بسیاری از مفاهیم ریاضی را به زبان ساده بیان کند، و اینبار برای اینکار از
اعداد کمک میگیرد. نام کتاب حاضر ”جهان شگفتانگیز اعداد“ است، ولی اینجا اعداد
فقط بهانهای هستند که به مفاهیمی بپردازد که در پشت این اعداد قرار دارند.
کتاب کار
خودش را با مفهوم عدد شروع میکند، سپس به معرفی پایههای مختلف عدد نویسی میپردازد.
بعد از آن نیز به سراغ دستگاههای مختلف اعداد میرود: کار را با اعداد طبیعی (یا
همان اعداد شمارشی) شروع میکند و به دستگاههای کاملتری مثل اعداد گویا، حقیقی،
مختلط، کواترنیونها، و اکتونیونها میرسد. برای اعدادی که در ریاضیات از اهمیت
ویژهای برخوردار هستند، مانند i،
e، π و
.... فصول جداگانهای در نظر گرفته شده است.
فصول این
کتاب به ترتیب عددی مرتب نشدهاند. در اینجا فصولی مانند ![]() ، -1، π و ...
داریم که خواه ناخواه نمیتوان آنها را بصورت عددی مرتب کرد، فصول این کتاب بیشتر
اوقات بر مبنای تاریخی مرتب شدهاند، بنابراین عناوین فصول را نباید به عنوان
ترتیب واقعی آنها در نظر گرفت.
، -1، π و ...
داریم که خواه ناخواه نمیتوان آنها را بصورت عددی مرتب کرد، فصول این کتاب بیشتر
اوقات بر مبنای تاریخی مرتب شدهاند، بنابراین عناوین فصول را نباید به عنوان
ترتیب واقعی آنها در نظر گرفت.
از
زمانهای دور اینطور پنداشته میشد که اساس همه چیزهای موجود در جهان اعداد هستند.
این تا اندازه زیادی درست است، ولی ما برای چیزهای مختلف پایههای گوناگونی داریم.
هر پایهای بر روی چیزی استوار شده که آنهم به نوبه خودش اصول و پایههای دیگری
دارد. از نظر خیلیها، اساسِ دانش بشر از علوم خالص سرچشمه میگیرند، و اساسِ علوم
نیز بر پایه ریاضیات بنا میشود، و چیزی هم که در ریاضیات نقش اساسی دارد اعداد
هستند. ولی همانطور که در ادامه این کتاب خواهید دید، امروزه اعداد بعنوان یکی از
ابداعات بشر شمرده میشوند، و این یعنی عدد نیز مانند بسیاری از چیزهای مطرح در
ریاضیات، تنها یک مفهوم ذهنی و مجرد است. در پایهایترین سطوح، اعداد نیز مانند
بقیه اشیاء ریاضی فقط یک مفهوم هستند، مفاهیمی که باید با اصول منطق سازگار باشند.
چیزی که بشر خیلی وقت است به آن پی برده این است که اساسترین چیزی که بر علوم (و
کلاً بر همه چیز) حکمفرما است، نه عدد است و نه ریاضیات، بلکه منطق است. اگر چیزی
از اصول منطق پیروی نکند و در آن تناقض وجود داشته باشد، در یک جای خود اشکال دارد
و باید به درستی آن شک کرد. در بخشهای پایانی این کتاب با اصول منطقی که مفهوم
عدد بر مبنای آنها پایه ریزی شده آشنا خواهید شد.
این کتاب
علاوه بر جنبههای ریاضی، جنبههای تاریخی زیادی نیز دارد. برای مطالعه بیشتر فصول
آن به پیشنیاز خاصی احتیاج نیست. برخی از بخشها نیز هستند که در آنها به فرمولهایی
اشاره شده که میتوان آنها را در کتابهای ریاضی دبیرستانی پیدا کرد. البته در این
کتاب به موضوعات پیشرفتهای نیز اشاره میشود، ولی فقط در حد مفاهیم کلی نه بیشتر.
واضح است که توضیحات فنی چنین مباحثی را نمیتوان در کتابی با این سطح گنجاند. در
کل هدف از اینگونه کتابها این است تا خواننده را با موضوعات جالبی که در ریاضیات
نوین مطرح هستند آشنا کند، و همچنین آنها را تشویق کند تا اگر هنوز رشته و گرایشی
را انتخاب نکردهاند، برای ادامه تحصیلات دانشگاهی خودشان ریاضیات را انتخاب کنند.
یان
استوارت ریاضیدان و مؤلف انگلیسی در سال 1945 در انگلستان بدنیا آمد، مدرک
کارشناسی خود را در رشته ریاضی از دانشگاه کمبریج دریافت کرد، سپس در سال 1967
برای گرفتن دکترای خود به دانشگاه وارویک (Warwick) رفت، و از آن پس نیز در همین دانشگاه مشغول تدریس و
تحقیق بوده است.
استوارت
از جمله نویسندگانی است که به ترویج دانش علمی، و بالاخص ریاضیات، شهرت دارد. از
وی بیش 10 کتاب درسی، 25 کتاب عمومی غیر تخصصی، و بیش از صد و پنجاه مقاله منتشر
شده. سری کتابهای (Discworld)،
که او با زیست شناس مشهور جک کوهن نوشته بسیار معروف و پر فروش هستند. تا
آنجا که مترجم مطلع است، تنها کتابهایی که از این نویسنده به زبان فارسی منتشر
شدهاند یکی کتاب
”چرا زیبایی واقعیت است؟“ و دیگری هم کتاب حاضر است.
کامران بزرگزاد
زمستان 1395
من همیشه
شیفته اعداد بودهام. خیلی پیش از اینکه به مدرسه بروم، مادرم خواندن و شمردن را
به من آموخته بود. به همین دلیل اولین روزی که به مدرسه رفتم در پایان روز از این
شکایت کردم که ”به ما هیچ چیزی یاد ندادند!“. تصور میکنم والدینم با گفتن این که
تو چیزهای جالبی را در مدرسه یادخواهی گرفت، مرا برای این روزِ سخت آماده کرده
بودند، و من هم این وعده را زیادی جدی گرفته بودم. ولی من خیلی زود موضوعاتی را
یاد گرفتم که چیزی از آنها نمیدانستم: سیارهها، دایناسورها، و اینکه چگونه با
خمیر مجسمه درست کنم... و چیزهای بیشتری نیز درباره اعداد یاد گرفتم.
من هنوز
هم افسون اعداد میشوم، و هنوز هم چیزهای بیشتری درباره آنها یاد میگیرم. من همیشه بر این تکیه میکنم که ریاضیات بیشتر از
اینکه درباره اعداد باشد، درباره بسیاری از تصورات متفاوت دیگری است، چیزهایی مثل:
اَشکال، الگوها، و احتمالات. ولی چیزی که همه اینها را پیریزی میکند اعداد
هستند. هر عدد برای خودش شخصیت منحصربفردی دارد. برخی از اعداد هستند که نسبت به
بقیه مرتبه بالایی دارند و در بسیاری از حوزههای نقش مهمی را ریاضیات بازی میکنند.
معروفترین آنها π
(عدد پی) است، که برای اولین بار وقتی با آن روبرو میشوید که با دایره سروکار
داشته باشیم. ولی این عدد تمایل شدیدی دارد تا در جاهایی ظاهر شود که اصلاً بنظر
نمیرسد با دایره ارتباطی داشته باشند.
برای
بیشتر اعداد نمیتوان چنین اهمیت بالایی را تصور کرد، ولی حتی شما غالباً برای
معمولیترین اعداد هم میتوانید ویژگیهایی را پیدا کنید. در کتاب ” The Hitchhiker’s Guide to the Galaxy“[1]،
از عدد 42 بعنوان پاسخ مسئله مهم ”زندگی، جهان، و همه
چیز“ یاد شده بود. داگلاس آدامز گفت که دلیل انتخاب او این بوده که دوستانش میگفتند
این عدد کاملاً بیفایده است. در واقع اینطور نیست، و ما دلیل آن را در فصل پایانی
کتاب نشان میدهیم.
این کتاب
بر اساس خود اعداد فصلبندی شده، گرچه ترتیب این اعداد در همه جا رعایت نشده.
همانطور که فصول 1، 2، 3،
و غیره وجود دارند، ما فصولی به نامهای 0، 42،
-1، ![]() ، π، و 43,252,003,274,489,856,000
و فصلی بنام
، π، و 43,252,003,274,489,856,000
و فصلی بنام ![]() خواهیم داشت. هر فصل با خلاصهای از موضوع اصلی شروع
میشود. اگر این خلاصهها خیلی واضح نبودند، یا در آنها احکام بیمزهای بود که
هیچ مدرکی برای اثبات آنها ارائه نشده، زیاد نگران نباشید، همانطور که مطالعه خود
را ادامه میدهید، همه آنها برایتان روشنتر خواهند شد.
خواهیم داشت. هر فصل با خلاصهای از موضوع اصلی شروع
میشود. اگر این خلاصهها خیلی واضح نبودند، یا در آنها احکام بیمزهای بود که
هیچ مدرکی برای اثبات آنها ارائه نشده، زیاد نگران نباشید، همانطور که مطالعه خود
را ادامه میدهید، همه آنها برایتان روشنتر خواهند شد.
ساختار
کتاب ساده است: هر فصل بر روی یک عدد جالب تمرکز میکند و توضیح میدهد که چرا این
عدد جالب است. برای نمونه، 2 به این دلیل جالب است
که در تمام ریاضیات، و همچنین در علوم، تمایز بین زوج و فرد را نشان میدهد. عدد 43,252,003,274,489,856,000 به این دلیل جالب است
که نمایانگر تعداد بازچینیهای مکعب روبیک (Rubik cube)
است.
چون 42
در این کتاب آمده، پس باید عدد جالبی باشد. خوب، این عدد به جهاتی که بعداً مشخص
میشود جالب است.
اعداد
نقطه شروع کار ما هستند، آنها مسیری را برای ما باز میکنند که میتوانیم ریاضیات
خاصی که این اعداد به آن وابسته هستند را تفحص کنیم. هر عددی برای خودش خاص است.
هنگامی که به مرحلهای برسید که قدر آنها را بعنوان اشخاص منحصربفرد بدانید، آنها
به دوستان قدیمیتان بدل خواهند شد. هر یک از آنها داستان خودش را دارد. معمولاً
این داستانها ما را به اعداد دیگری هدایت میکند، ولی چیزی که واقعاً اهمیت دارد،
آن ریاضیاتی است که آنها را به هم پیوند میدهد. اعداد شخصیتهای یک نمایشنامه
هستند، و چیزی که بیشترین اهمیت را دارد خود نمایشنامه است. اما مسئله این است که
شما بدون وجود شخصیتهای مختلف نمیتوانید یک نمایشنامه داشته باشید.
برای
جلوگیری از نابسامانی بیشتر، من کتاب را بر حسب نوع اعداد به بخشهای مختلفی تقسیم
کردهام. اعداد صحیح کوچک، کسرها، اعداد حقیقی، اعداد مختلط، بینهایتها ... . به
غیر از چند مورد استثناء که اجتناب ناپذیر بوده، کتاب بر اساس یک ترتیب منطقی
تنظیم شده. حتی اگر موضوعات فصلهای بعدی نیز بکلی تغییر کند، باز هم فصلهای قبلی
پایهای برای فصلهای بعدی هستند. این نیاز بر روی چگونگی مرتب کردن فصول تاثیر
داشته، و در این میان به مصالحههایی نیاز بوده. مهمترین آنها شامل اعداد مختلط میشود.
سر و کله این اعداد خیلی زود پیدا میشود، زیرا من برای بحث در مورد بعضی از اعداد
معمولیتر به آنها نیاز دارم. بطور مشابه، در بعضی جاها نیز یک موضوع پیشرفته مطرح
میشود، زیرا تنها جای معقولی که میتوان به آن اشاره کرد در همانجا بوده. اگر به
چنین مطالبی برخورد کردید و آنها را دشوار دیدید، آنها را نادیده گرفته و به
بخشهای بعدی بروید. بعداً دوباره میتوانید به آنها بازگردید.
اعداد
حقیقتاً شگفتانگیز هستند، نه از این نظر که داستانهایی که در مورد آنها وجود
دارند باور نکردنی هستند، بلکه آنها از جنبه مثبت شگفت انگیزاند: عوامل معینی برای
شگفتانگیز بودن آنها وجود دارد. و شما میتوانید بدون اینکه چیزی را حساب کنید،
این شگفتی را حس کنید. شما میتوانید ببینید که چگونه اعداد در طول تاریخ تحول
پیدا کردهاند، زیبایی الگوهای نهفته در آنها را تحسین کنید، ببینید کاربرد آنها
چیست، و
مثلاً پیش خود بگویید ”من اصلاً فکر نمیکردم 56
اینقدر جالب باشد!“ ولی همینطور است، واقعاً اینطور است.
همه اعداد
جالباند، از جمله 42.
چه چیزی
میتواند سادهتر از 1, 2, 3, 4, 5, 6, 7, . .
.
باشد؟ با اینحال شاید هنوز هم این اعداد هستند که بیش از هر چیز
دیگری بشر را قادر ساختهاند تا خودش را از این کره خاکی کنده و به عرش برساند. تک
تک اعداد شخصیتِ خاصِ خود را دارند و ما را به حوزههای مختلف ریاضیات هدایت میکنند.
اما پیش از اینکه آنها را یک به یک بررسی کنیم، مفید خواهد بود تا توجه خودمان را
به سه سؤال اساسی معطوف کنیم. منشاء اعداد چه بوه؟ مفهوم عدد چگونه توسعه یافته؟ و نهایتاً اینکه اعداد چه
هستند؟
در حدود
35000 سال پیش، در دوران دیرینه سنگی، بر روی استخوان یک بابون[2] که در سلسله جبال لِبومبو (Lebombo Mountains) سویس یافت شد و اکنون به استخوان لِبومبو
شناخته میشود، انسان ناشناسی 29 علامت را حک کرد. تصور میشود که این استخوان
نوعی چوبخط بوده (چوبخط یک چوب گرد و دراز است که برای ضبط اعداد و حسابها،
شکافهایی به شکل |، ||، |||،
و غیره در آن ایجاد میشده). در ماه قمری 29.5 روز وجود دارد،
بنابراین این چوب میتوانسته نوعی تقویم قمری ابتدایی باشد، یا چیزی که دوره عادت
ماهیانه زنان را ضبط میکرده.
استخوان
دیگری که به استخوان گُرگ معروف است، 55 نشانه دارد. این استخوان قدمتی 30000 ساله
دارد و در سال 1937 در
چكوسلواكي پیدا شد.
در سال
1960 زمینشناس بلژیکی ژان دو براکور (Jean de braucourt)، یک استخوان بابون را در
میان بقایای یک جامعه ماهیگیر کشف کرد که بوسیله گدازههای یک آتشفشان پوشیده شده
بود. مکان کشف این استخوان ایشانگو (Ishango)
بود، جایی که اکنون در میان اوگاندا و کونگو قرار دارد. قدمت این استخوان حدود
20000 سال برآورد شده.
در اینجا نیز سادهترین تعبیری که برای استخوان
ایشانگو ارائه شد چوبخط بودن آن بود. برخی از مردمشناسان از این فراتر رفته و
عناصری از ساختارهای حسابی مانند ضرب، تقسیم، و اعداد اول را در آن دیدهاند. برخی
فکر میکنند این یک تقویم شش ماهه است، برخی نیز باور دارند که این تنها یک ابزار
ساخته شده از استخوان است و این شکافها تنها برای بهتر نگاه داشتن ابزار در آن حک
شده، و اهمیت ریاضی خاصی ندارد.

شکل 1: تصویری از استخوان ایشانگو که در موزه ملی بلژیک
نگهداری میشود.
مطمئناً
این کنجاویبرانگیز است. در اینجا سه دسته شکاف وجود دارند. دسته مرکزی از اعداد 3, 6, 4, 8, 10, 5, 7 استفاده میکند. 6
دو برابر 3، و 8 دو برابر 4،
و 10 دو برابر 5 است، ولی ترتیب این
آخری وارونه شده، و 7 که در آخر آمده نیز هیچ
الگویی ندارد. دسته سمت چپ شامل 11, 13,
17, 19 است، یعنی اعداد اول بین 10 تا20 .
دسته سمت راست شامل اعداد فرد 11, 21,
19, 9 است. مجموع اعداد موجود در سمت راست، و نیز سمت چپ، هر دو 60
است.
مشکلی که
با چنین تعابیری وجود دارد این است که میتوان در هر دنباله کوچکی از اعداد چنین
الگوهایی را پیدا کرد. برای نمونه در جدول 1 لیستی از جزایر دهگانه باهاما، به
همراه مساحت آنها آمده است. برای اینکه هیچ ترتیب ریاضی بخصوصی در کار نباشد، من
این جزایر را بر حسب نام آنها مرتب کردهام. به شما قول میدهم که هیچ قصد خاصی از
این مرتبسازی نداشتم و این اولین چیزی بود که به فکرم رسید، اگر ترتیب دیگری بود
که منظور مرا بهتر میرساند، قطعاً از آن استفاده میکردم، ولی نیازی به آن نیست،
و من هم اینکار را نکردم.
نام جزیره
مساحت بر حسب مایل مربع
Berry 12
Bimini 9
Crooked Island 93
Little Inagua 49
Mayaguana 110
New Providence 80
Ragged Island 14
Rum Cay 30
Samana Cay 15
San Salvador Island 63
جدول 1
آیا ما در اینجا الگوی عدد خاصی را مشاهده میکنیم؟
در اینجا تعداد زیادی دنبالههای کوتاه وجود دارند که خصوصیات مشترکی دارند:

شکل 2: برخی از الگوهای ظاهری که در مساحتهای جزایر
باهاما مشاهده میشوند.
برای شروع
باید گفت که تقارن زیبایی در تمامی لیست وجود دارد. در هر دو سمت مضارب 3
دیده میشود. در وسط یک جفت مضرب 10 آمده که مضارب 7
را از هم جدا میکند. بعلاوه دو عدد مربع نیز در اینجا دیده میشوند: 9= 32
و 47=72
که هر دو مربعهای اعداد اول
هستند. در همان حوالی، اعداد 15 و 30
قرار دارند که یکی دو برابر دیگری است. در دنباله 9–93–49 همه اعداد شامل رقم 9 هستند. به غیر از
دنباله 110–80–14،
اعداد به ترتیب بزرگتر و کوچکتر میشوند. و نهایتاً اینکه، آیا متوجه شدهاید که
هیچ کدام از اعداد اول نیستند؟
به اندازه
کافی گفتم. مشکل دیگری که در مورد استخوان ایشانگو وجود دارد عدمامکان پیدا کردن
شواهد اضافی برای پشتیبانی از هر تعبیر خاصی از آن است. ولی در هرحال، حکاکیهایی
که بر روی این استخوان وجود دارند کنجکاوی برانگیزاند. بقیه جداول معماهای عددی
نیز چنین خاصیتهایی را دارند.
ده هزار
سال قبل مردمان خاور نزدیک برای نوشتن اعداد از نشانههای رُسی استفاده میکردند
تا شاید برای ثبت مالیات یا سند مالکیت از آنها استفاده کنند. قدیمیترین نمونههای
آن را میتوان در سلسله جبال زاگرس ایران، در دو مکان به نامهای تپه آسیاب،
و تپه گنج دَره مشاهده کرد. این نشانهها تکههای کوچکی از رُس با اندازههای
متفاوت بودند، که بر روی برخی از آنها نمادهایی حک شده بود. یک گوی که علامت + روی
آن بود، نشانده یک گوسفند است. هفت تا از این گویها نشانه هفت گوسفند بودند. برای
پرهیز از طولانی شدن چنین علامتهایی، برای نشان دادن ده گوسفند از نماد جداگانهای
استفاده میشد. ولی برای نشان دادن ده چیز دیگر، مثلاً ده بُز، یا چیزهای دیگر از
نماد متفاوتی استفاده میشد.
از 4000
سال قبل از میلاد، این نشانهها مانند مهرههای یک گردنبند پشت سرهم در یک ریسمان
قرار میگرفتند. ولی بدلیل اینکه با اضافه کردن یا برداشتن این مهرهها میشد
اعداد را تغییر داد، بنابراین برای آن تمهیدادت امنیتی نیز ابداع شد. مهرهها در
لایهای از خاک رُس پیچیده میشدند، که در کوره قرار میگرفت و پخته میشد. هر نوع
اختلافی که بر سر اعداد بود، میتوانست با شکستن لفاف رُسی و باز کردن آن حل شود.
از 3500 سال قبل از میلاد، برای جلوگیری از شکستنهای غیرضروری لفافههای رُسی،
ماموران اداری بینالنحرین باستان شروع به نوشتن نمادهایی بر روی خود لفافه کردند
که محتوای علامتهای درون آن را نشان میداد.
از آن زمان ناگهان این ایده قوت گرفت که گویهایی که
نمادها بر روی حک شدهاند یک چیز اضافی هستند. نتیجه این شد که علائم عددی بوجود
آمد، و متعاقب آن، راه برای نوشتن دستگاههای عدد نویسی، و احتمالاً خود نوشتن،
هموار شد.

شکل 3: لفافه رُسی و نمادهای درون آن، مربوط به دوران
اوروک (Uruk period)، در منطقه شوش
ایران.
کتاب حاضر
عمدتاً یک کتاب تاریخی نیست، بنابراین من به دستگاههای عدد نویسی در ارتباط با
بوجودآمدن آنها از اعداد خاص نگاه خواهم کرد. بعنوان نمونه، در فصل [10] عددنویسی قدیم و جدید دهدهی (اعشاری) بررسی خواهند شد. ولی همانگونه که
ریاضیدان بزرگ آلمانی کارل فردریش گاوس بیان میکرد ” نماد گذاری مهم نیست، آنچه مهم است مفهوم
این نمادها است[3]“،
موضوعات آتی هنگامی ملموستر میشوند که به آنها از زمینه تغییر ادراک انسان از
اعداد نگریسته شود. بنابراین ما کار خود را با نگاه سریعی به دستگاههای عمده عدد
نویسی و برخی اصطلاحات مهم آغاز میکنیم.
ما تمایل
داریم که اعداد را بعنوان چیزهایی ثابت و تغییرناپذیر درنظر بگیریم، یعنی یکی از
همان خصوصیاتی که جهان مادی دارد. در واقع اعداد نیز یکی از اختراعات بشر هستند،
ولی از نوع بسیار مفید آن، زیرا آنها بیانگر جنبههای مهم جهان مادی هستند؛ مثلاً
اینکه شما دارای چند گوسفند هستید، یا سن جهان چقدر است. جهان با روبرو کردن ما با
مسائل جدید، مکرراً ما را شگفتزده میکند، مسائلی که پاسخ به آنها نیازمند
مفاهیمِ جدیدِ ریاضی است. برخی اوقات هم این نیازهای درونی خود ریاضیات که ما را
به سمت ساختارهای بالقوه مفیدی راهنمایی میکند. هر از چند گاهی این مسائل و
راهنماییها منجر به این میشود تا ریاضیدانان با اختراع گونههای جدیدی از اعداد،
دستگاههای اعداد را توسعه دهند.
ما دیدهایم
که چگونه نیاز به شمردن چیزها منجر به اختراع اعداد شد. در دوران اولیه یونان
باستان، فهرست اعداد با 2، 3،
4، ... شروع میشد. 1
آنقدر خاص بود که حقیقتاً عدد بشمار نمیرفت. بعدها که این عرف مسخره بنظر آمد، 1
نیز یک در زمره اعداد درآمد. قدم بعدی در گسترش دستگاه اعداد، معرفی کسرها بود.
این نوع اعداد هنگامی مفید هستند که مثلاً بخواهید کالاهایی را میان چندین نفر
تقسیم کنید. اگر سه نفر بخواهند از دو پیمانه گندم سهم مساوی بگیرند، هر یک باید
به اندازه ![]() پیمانه سهم بگیرند.
پیمانه سهم بگیرند.

شکل 4. سمت چپ: حروف تصویری مصری (هیروگیریف) برای
![]() و
و ![]() .
وسط: چشم بوتو (Wadjet eye).
سمت راست: هیروگیریفهای کسری
برگرفته شده از تصویر.
.
وسط: چشم بوتو (Wadjet eye).
سمت راست: هیروگیریفهای کسری
برگرفته شده از تصویر.
مصریان
باستان کسرها را به سه طریق مختلف نمایش میدادند. آنها برای ![]() و
و ![]() هیروگریفهای خاصی داشتند. آنها برای نمایش تقسیم 1
بر شش توان نخست 2 (یعنی 2,4,8,16,32,64)
از بخشهای مختلف چشم بوتو استفاده میکردند. سرانجام آنها نمادهایی را برای
کسور واحد ابداع کردند (کسور واحد آنهایی هستند که در آنها عدد 1مقسوم است و بر روی اعداد دیگر مینشیند،
مانند:
هیروگریفهای خاصی داشتند. آنها برای نمایش تقسیم 1
بر شش توان نخست 2 (یعنی 2,4,8,16,32,64)
از بخشهای مختلف چشم بوتو استفاده میکردند. سرانجام آنها نمادهایی را برای
کسور واحد ابداع کردند (کسور واحد آنهایی هستند که در آنها عدد 1مقسوم است و بر روی اعداد دیگر مینشیند،
مانند: ![]() ،
،
![]() ،
،
![]() ،
و ...). آنها تمام کسور دیگر را بعنوان مجموعهای جداگانهای از کسور واحد نمایش
میدادند. برای نمونه،
،
و ...). آنها تمام کسور دیگر را بعنوان مجموعهای جداگانهای از کسور واحد نمایش
میدادند. برای نمونه،
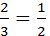 +
+ ![]()
مشخص نیست
که چرا آنها ![]() را بصورت
را بصورت ![]() ننوشتهاند.
ننوشتهاند.
سر و کله
عدد صفر بعدها پیدا شد، احتمالاً به این دلیل که نیاز اندکی برای آن بود. اگر شما
هیچ گوسفندی نداشته باشید، نیازی هم به شمردن یا فهرست کردن آنها وجود ندارد. صفر
ابتدا بعنوان یک نماد معرفی شد، و عدد هم بحساب نمیآمد. ولی هنگامی که ریاضیدانان
چینی و هندی اعداد منفی را معرفی کردند، 0 نیز میبایست بعنوان
یک عدد درنظر گرفته میشد، دلیل آن هم این بود چون مجموع دو عدد، خود یک عدد است،
پس 0 نیز باشد عدد باشد، برای مثال، 1+(-1)=0.
ریاضیدانان
دستگاه اعداد زیر را اعداد طبیعی (natural numbers)
مینامند:
0, 1, 2, 3, 4, 5, 6, 7, .
. .
و هنگامی
که اعداد منفی را به این مجموعه اضافه کنیم، اعداد صحیح (integers)
حاصل میشود.
... ; 3; 2; 1; 0; 1; 2; 3; ...
اعداد
کسریِ مثبت، اعداد کسریِ منفی، و صفر بر روی هم اعداد گویا (rational)
را تشکیل میدهند. یک عدد هنگامی مثبت است که از صفر بزرگتر باشد، و منفی است اگر
از صفر کوچکتر باشد. بنابراین تمام اعداد (چه صحیح باشد چه گویا) در یکی از این سه
دسته قرار میگیرد: مثبت، منفی، یا صفر.
اعداد
شمارشی، یعنی 1, 2, 3, 4, 5, 6, 7, . . .،
اعداد صحیح مثبت هستند. چنین عرفی ما را به یک اصطلاح زمخت دیگری هدایت میکند: اعداد طبیعی یا اعداد
کامل، یعنی: 0, 1, 2, 3, 4, 5, 6, 7, . . .،
به اعداد صحیح غیر-منفی نیز معروف
هستند.
برای
مدتها، کسور حداعلی چیزی بودند که میشد آن را به عنوان عدد تصور کرد. ولی
یونانیان باستان ثابت کردند که نمیتوان کسری را پیدا کرد که مجذور آن دقیقا با 2
برابر باشد. بعدها این مسئله به اینصورت بیان شد که ”![]() یک عدد گنگ (irrational)
است“، یعنی این عدد گویا نیست. یونانیان برای بیان این مسئله راه طاقت فرسایی را
طی کردند، ولی آنها میدانستند که
یک عدد گنگ (irrational)
است“، یعنی این عدد گویا نیست. یونانیان برای بیان این مسئله راه طاقت فرسایی را
طی کردند، ولی آنها میدانستند که ![]() باید وجود داشته باشد. قضیه فيثاغورث میگوید این
عدد باید طول قطر مربعی باشد که اضلاع آن برابر 1 هستند. بنابراین به
اعداد مختلفی نیاز بود. یونانیان برای کار با اعداد گنگ یک روش پیچیده هندسی
یافتند، ولی این روش کاملاً رضایتبخش نبود.
باید وجود داشته باشد. قضیه فيثاغورث میگوید این
عدد باید طول قطر مربعی باشد که اضلاع آن برابر 1 هستند. بنابراین به
اعداد مختلفی نیاز بود. یونانیان برای کار با اعداد گنگ یک روش پیچیده هندسی
یافتند، ولی این روش کاملاً رضایتبخش نبود.
در راه
رسیدن به مفهوم جدید اعداد، قدم بعدی اختراع ممیز و نوشتن اعداد کسری بصورت اعداد
ممیز دار بود. این باعث شد تا بتوان اعداد گنگ را با دقتی بسیار بالا توسط اعداد
ممیزدار نمایش داد. برای مثال، عدد ![]() را میتوان بصورت زیر نوشت:
را میتوان بصورت زیر نوشت:
![]() *1.4142135623
*1.4142135623
که تا 10
رقم اعشار صحیح است (در اینجا علامت *
به معنای ”تقریباً معادل است با“ میباشد). این عبارت دقیق نیست، زیرا مجذور آن
عدد 1·99999999979325598129
میشود.
تقریب دیگری
از ![]() که تا 20 رقم صحیح است بصورت زیر میباشد:
که تا 20 رقم صحیح است بصورت زیر میباشد:
![]() *1.41421356237309504880
*1.41421356237309504880
ولی عدد
فوق نیز دقیق نیست. ولی یک حسِ قوی منطقی هست که به ما میگوید ”اگر دنباله بینهایتی
از بسط اعشاری این عدد داشته باشیم، چنین عددی دقیق است“. البته واضح است که چنین
عبارتی نمیتواند بطور کامل نوشته شود، ولی میتوان از آن اینطور برداشت کرد که
چنین چیزی درست است.
اعداد
اعشاری بینهایت دراز (حتی آنهایی که این بسط در آنها متوقف میشود، و میتوان
ادامه عدد را دنبالهای از 0های بیپایان در نظر گرفت) به اعداد حقیقی (real
numbers) معروف هستند. به این دلیل به آنها اعداد حقیقی گفته میشود
که از آنها برای اندازهگیری جهان واقعی استفاده میشود، چیزهایی مثل طول و وزن.
هر قدر که بخواهید این اندازهگیریها دقیقتر باشد، به اعدادِ اعشاری نیاز دارید
که رقمهای بیشتری دارند. شما برای دستیابی به مقداری که کاملاً دقیق باشد، به
بینهایت رقم نیاز داریید. شاید این طعنهآمیز باشد که صفت ”حقیقی“ که به این نوع
اعداد داده شده باید با ارقام بینهایت درازی تعریف شود که حقیقتاً نمیتوان آنها
را نوشت. ما همچنین میتوانیم اعداد حقیقی منفی نیز داشته باشیم.
تا قرن
هجدهم میلادی، به غیر از اعداد حقیقی هیچ شکل دیگری از اعداد نمیتوانست واقعی
باشد. ولی حتی از قرن پانزدهم به بعد نیز برخی از ریاضیدانان کنجکاو بودند که آیا
ممکن است نوع جدیدی از اعداد وجود داشته باشند یا نه. این عدد جدید ریشه دوم -1
بود، یعنی همان عددی که اگر آن را در خودش ضرب کنیم، حاصل آن -1
میشود. در نگاه اول چنین چیزی دیوانهورا بنظر میرسد، زیرا مجذور هر عدد حقیقی
یا مثبت است یا صفر. ولی معلوم شد که بکارگیری جذر -1، که لئونارد اویلر (Leonhard
Euler) علامت i
را برای آن معرفی کرد، ایده بسیار خوبی است. حرف i در بسیاری از زبانهای
اروپایی، حرف اول لغت ‘imaginary’
به معنای موهومی است. بدلیل اینکه ریاضیدانان میخواستند این اعداد را از اعداد
حقیقی قدیمی متمایز کنند، برای نامیدن آنها از نام موهومی استفاده شد.
ولی متاسفانه این نامگذاری به رمز و رازهای منتهی شد که ضرورتی برای آنها نبود. گوتفرید لایبنیتز (Gottfried
Leibniz) یکبار درباره i گفته بود که ”این عدد موجودی
است ذوحیاتین که مابین بودن و نبودن قرار دارد“. این باعث مخدوش شدن یک واقعیت
عمده شد، و آن اینست که هم اعداد حقیقی و هم اعداد موهومی هر دو دارای وضعیت منطقی
یکسانی هستند. هر دو آنها مفاهیمی انسانی هستند که واقعیتهای جهانِ مادی
را مدلسازی میکنند، ولی هیچ یک از آنها واقعی نیستند.
وجود i باعث شد تا برای
انجام محاسبات، اعداد جدید بسیاری بوجود آیند، اعدادی مانند 2+3i
که به آنها اعداد مختلط (complex numbers) گفته میشود و در
چند قرن اخیر از اجزاء ضروری ریاضیات و علوم بحساب میآیند. برای بسیاری از انسانها،
این واقعیتِ عجیب تازگی دارد، زیرا شما غالباً در ریاضیات دبیرستانی با چنین
اعدادی برخود نمیکنید. دلیل این مسئله این نیست که آنها مهم نیستند، بلکه ایدههایی
که آنها بر آن بنا شدهاند پیچیده هستند و کاربرد آنها نیز پیشرفته است.
ریاضیدانان از علامتهای عجیبی برای نشان دادن دستگاههای اصلی اعداد استفاده میکنند.
من در این کتاب از آنها استفاده نمیکنم، ولی بهتر است شما با آنها آشنا باشید:
N: مجموعه همه اعداد طبیعی 0,
1, 2, 3, . . .
Z : مجموعه همه اعداد صحیح … ,-3, -2, -1, 0, 1, 2
,3 …
Q: مجموعه همه اعداد گویا
R: مجموعه همه اعداد حقیقی
C: مجموعه
همه اعداد مختلط
مانند
عروسکهای روسی که در دل یکدیگر جای میگیرند، این مجموعهها نیز به ترتیب زیر در دل دیگری قرار گرفتهاند:
N
Ì Z Ì
Q Ì
R Ì
C
علامت Ì در نظریه مجموعهها به معنای ”میگنجد در“ است. توجه داشته باشید که مثلاً هر عدد
صحیح یک عدد گویا نیز هست؛ مثلاً عدد صحیح 3، کسر ![]() نیز هست. ما معمولاً 3 را بصورت کسری نمینویسیم،
هرچند که هر دو اینها یک عدد را نمایش میدهند. به همین نحو، هر عدد گویا یک عدد
حقیقی نیز هست، و هر عدد حقیقی نیز یک عدد مختلط است. دستگاههای قدیمی اعداد
بجای اینکه با دستگاههای جدیدی جایگزین شوند در داخل آنها قرار میگیرند. دستگاههای
مختلف اعداد توسط ریاضیدانان در طول قرنها گسترش یافتهاند، ولی حتی اعداد مختلط
نیز به معنای پایان این گسترش نیست. برای نمونه ما اعداد چهارگانه یا کواترنیونها (quaternions)
و اعداد هشتگانه یا ُاکتونیونها (octonions) را داریم، که به
ترتیب با علامتهای H و O نشان
داده میشوند[4] . ولی اینگونه اعداد بیشتر از اینکه از لحاظ حسابی فایدهای
داشته باشند، بیشتر از نظر جبری مفیدند. در پایان این بخش میخواهم به عددی اشاره
کنم که بیشتر از اینکه حالت یک عدد را داشته باشد، حالت یک معما را دارد، و آن
چیزی نیست جز بینهایت (infinity).
از نظر فلسفی، بینهایت با اعداد معمولی تفاوت دارد و به هیچ یک از دستگاههای
مرسوم اعداد، از اعداد طبیعی گرفته تا مختلط، تعلق ندارد. با اینحال میان حاشیهها سرگردان است، و یک
شبیه-عدد است، ولی آنچنان که باید یک عدد نیست. وقتی جورج کانتور (Georg Cantor) درک اولیه ما را از
مفهوم شمارش تغییر داد، معلوم شد که از نظر شمارشی، بینهایت نه فقط یک عدد است،
بلکه بینهایت میتواند اندازههای متفاوتی داشته باشد. در میان این اندازههای
مختلف، ما À0 را داریم که نشان
دهنده تعداد اعداد کامل، و c که نشان دهنده تعداد
اعداد حقیقی است. کدام یک از این دو بزرگتراند ؟ مسئله همین بزرگتر بودن است، و به این
بستگی دارد که شما برای صورتبندی ریاضیات از چه دستگاهِ اصلِ موضوعی (axiom)
استفاده میکنید.
نیز هست. ما معمولاً 3 را بصورت کسری نمینویسیم،
هرچند که هر دو اینها یک عدد را نمایش میدهند. به همین نحو، هر عدد گویا یک عدد
حقیقی نیز هست، و هر عدد حقیقی نیز یک عدد مختلط است. دستگاههای قدیمی اعداد
بجای اینکه با دستگاههای جدیدی جایگزین شوند در داخل آنها قرار میگیرند. دستگاههای
مختلف اعداد توسط ریاضیدانان در طول قرنها گسترش یافتهاند، ولی حتی اعداد مختلط
نیز به معنای پایان این گسترش نیست. برای نمونه ما اعداد چهارگانه یا کواترنیونها (quaternions)
و اعداد هشتگانه یا ُاکتونیونها (octonions) را داریم، که به
ترتیب با علامتهای H و O نشان
داده میشوند[4] . ولی اینگونه اعداد بیشتر از اینکه از لحاظ حسابی فایدهای
داشته باشند، بیشتر از نظر جبری مفیدند. در پایان این بخش میخواهم به عددی اشاره
کنم که بیشتر از اینکه حالت یک عدد را داشته باشد، حالت یک معما را دارد، و آن
چیزی نیست جز بینهایت (infinity).
از نظر فلسفی، بینهایت با اعداد معمولی تفاوت دارد و به هیچ یک از دستگاههای
مرسوم اعداد، از اعداد طبیعی گرفته تا مختلط، تعلق ندارد. با اینحال میان حاشیهها سرگردان است، و یک
شبیه-عدد است، ولی آنچنان که باید یک عدد نیست. وقتی جورج کانتور (Georg Cantor) درک اولیه ما را از
مفهوم شمارش تغییر داد، معلوم شد که از نظر شمارشی، بینهایت نه فقط یک عدد است،
بلکه بینهایت میتواند اندازههای متفاوتی داشته باشد. در میان این اندازههای
مختلف، ما À0 را داریم که نشان
دهنده تعداد اعداد کامل، و c که نشان دهنده تعداد
اعداد حقیقی است. کدام یک از این دو بزرگتراند ؟ مسئله همین بزرگتر بودن است، و به این
بستگی دارد که شما برای صورتبندی ریاضیات از چه دستگاهِ اصلِ موضوعی (axiom)
استفاده میکنید.
ولی
بیایید تا وقتی شناخت کافی از اعداد معمولیتر کسب نکردهایم، بررسی اینها را به
بعد موکول کنیم، و همین است که ما را به پرسش سومی که مطرح کردم میرساند.
این سؤال
سادهای بنظر میرسد، و همینطور هم هست. ولی جواب آن ساده نیست! همه ما میدانیم
که چگونه از اعداد استفاده کنیم، همه ما میدانیم که هفت گاو، یا هفت گوسفند، یا هفت
صندلی چطور بنظر میرسد. همه ما میتوانیم تا هفت بشماریم. ولی خود هفت چیست؟ پاسخ
این سؤال علامت 7 نیست. این یک علامت اختیاری است و در زبانهای مختلف
متفاوت است. مثلاً در زبان عربی/فارسی این عدد را با 7، و در زبان چینی آن را با七 و یا 柒 نشان
میدهند. معنای این عدد لغت ’هفت‘ هم نیست، چه آن هم در زبانهای مختلف
متفاوت است. در زبان فرانسوی به آن sept و در آلمانی به آن sieben میگویند. در
حوالی نیمه قرن نوزدهم، تعدادی از ریاضیدانان و منطقدانان دریافتند که اگرچه
برای هزاران سال همه به آسانی از اعداد استفاده کردهاند، ولی کسی واقعاً نمیداند
که آنها چیستند. بنابراین آنها سؤالی را مطرح کردند که هیچ وقت نباید پرسیده میشد،
و آن این بود که یک عدد چیست؟ این سؤال دشوارتر ا آن است که بنظر میرسد.
یک عدد چیزی نیست که شما بتوانید در دنیای واقعی آن را به کسی نشان دهید. عدد نوعی انتزاع (abstraction)
است، یعنی یک مفهوم ذهنی انسانی، چیزی که از واقعیت جهان خارج برگرفته میشود ولی
در واقع خودش واقعی نیست. چنین چیزی ممکن است نگران کننده بنظر برسد، ولی اعداد از
این لحاظ تنها نیستند. یک نمونه آشنا از این نوع ’پول‘ است. همه ما میدانیم که
چطور بهای چیزی را پرداخت کنیم و بقیه پول خود را پس بگیریم، و (پیش خود فکر میکنیم)
اینکار را با تبادل پول انجام میدهیم. بنابراین تمایل ما این است که پول را
بعنوان سکهها و اسکناسهایی که در جیبمان قرار دارند در نظر بگیریم. ولی مفهوم
پول به این سادگی هم نیست. اگر ما از کارتهای بانکی استفاده کنیم، هیچ سکه یا
اسکناسی رد و بدل نمیشود. در عوض سیگنالهایی از خطوط ارتباطی عبور کرده و به بانک
مربوطه میرسد، و در چندین حساب (از جمله حساب ما و فروشنده) عددهایی تغییر میکنند.
یک اسکناس پنج دلاری در بردارنده این مضمون است که ”من عهد میکنم که مبلغ پنج
دلار به حامل این اسکناس پرداخت کنم“. این اسکناس به هیچ وجه پول نیست، بلکه عهدی
برای پرداخت پول است. زمانی بود که شما میتوانستید آن را به بانک ببرید و در ازاء
آن طلا دریافت کنید. در آن زمانها این طلا بود که پول واقعی بشمار میرفت. ولی
طلا هم پول واقعی نبود، بلکه تجسم فیزیکی آن بود. بعنوان اثبات این موضوع میتوان
به ثابت نبودن ارزش طلا اشاره کرد. آیا پول یک عدد است؟ پاسخ مثبت است، ولی تنها
در یک زمینه قانونی خاص. نوشتن یک میلیون دلار بصورت $1,000,000
بر روی یک تکه کاغذ باعث نمیشود شما یک میلیونر شوید! آنچه پول را پول میکند
مجموعه قراردادهای انسانی در این درباره است که ما چگونه عدد پول را نمایش میدهیم،
و چگونه آن را با کالاها یا اعداد دیگر مبادله میکنیم. اینکه خود پول چیست مهم
نیست، مهم چیزی است که شما با آن انجام میدهید. پول یک انتزاع است. اعداد هم
همینطور. ولی این جواب چندان مناسبی نیست، زیرا کُل ریاضیات یک انتزاع است.
بنابراین برخی ریاضیدانان میپرسیدند که چه نوع انتزاعی میتواند ’عدد‘ را
تعریف کند در سال 1884 ریاضیدان آلمانی گوتلوب فرگه (Gottlob
Frege) کتاب مبانی حساب[4] را نوشت و در آن اصول بنیادی ریاضیات را، که
بر اساس اعداد قرار داشت، بنا نهاد. 10 سال بعد او جلوتر رفت، و تلاش کرد این اصول
را از قوانین منطق، که قوانین اصولیتری بودند، نتیجه بگیرد. کتاب قوانین پایهای
حساب[5] او در دو جلد بترتیب در سالهای 1893 و 1903 منتشر
شد.
فرگه کار خود را با روند شمارش آغاز کرد، و تمرکز
خود را نه بر روی اعداد، بلکه بر روی چیزهای که میشماریم گذاشت. اگر من هفت فنجان
را بر روی میز بگذارم و آنها را بصورت ‘1, 2, 3, 4, 5, 6, 7’
بشمارم، اشیایی که مهم بنظر میرسند این اعداد هستند. ولی فرگه مخالف بود، او به
فنجانها فکر میکرد. عمل شمارش به این دلیل کار میکند که ما مجموعهای از فنجانها
را داریم که میخواهیم آنها را بشماریم. اگر مجموعه متفاوتی داشته باشم، ممکن است
از این شمردن عدد دیگری را حاصل کنیم. فرگه این مجموعهها را کلاس (class)
نامید. هنگامی که میخواهیم تعداد فنجانهایی را که در این کلاس خاص قرار دارند را
بشماریم، ما تناظری (correspondence) بین کلاس فنجانها و علامتهای 1, 2, 3, 4, 5, 6, 7 برقرار میکنیم.
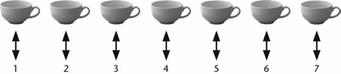
شکل 5. تناظر میان فنجانها و علائم عددی.
همینطور
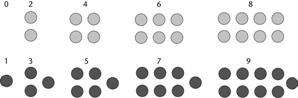
اگر یک کلاس نعلبکی هم داشته باشیم، بازهم میتوانیم چنین تناظری را برقرار کنیم:

شکل 6. تناظر میان نعلبکیها و ارقام
اگر چنین
باشد، ما میتوانیم نتیجه بگیریم که کلاس نعلبکیها همان تعدادی را دربر دارد که
کلاس فنجانها. ما حتی این تعداد را میدانیم: هفت.
ممکن است چنین چیزی آنقدر واضح باشد که اشاره به آن
بیفایده بنظر آید، ولی فرگه دریافت که این مورد چیز کاملاً ژرفی را به ما میگوید.
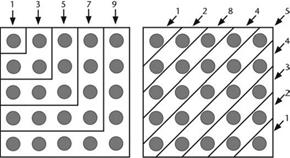
مثلاً ما میتوانیم ثابت کنیم که کلاس نعلبکیها همان تعداد نعلبکی را در بردارد
که کلاس فنجانها در خود فنجان دارد، آنهم بدون کاربرد علامتهای 1,
2, 3, 4, 5, 6, 7 و بدون اینکه بدانیم چه تعداد نعلبکی یا فنجان آنجا
هستند. کافیست تناظری بین کلاس فنجانها و کلاس نعلبکیها برقرار کرد:

شکل 7. تناظر بین فنجانها و نعلبکیها نیازی به
اعداد ندارد.
اصطلاحاً
چنین تناظری” تناظر یک-به-یک (correspondence one-to-one)“
نامیده میشود: یعنی هر فنجان دقیقاً با یک نعلبکی مطابق است، و هر نعلبکی هم
دقیقاً با یک فنجان. اگر شما یک فنجان را از قلم بیاندازید، یا یک فنجان را چندین
بار بشمارید، عمل شمارش درست کار نمیکند. اجاز دهید تا با درنظر گرفتن شرایط فوق،
این را فقط ’تناظر‘ بنامیم.
ضمناً اگر
هیچ موقع فکر کردهاید که چرا بچههای دبستانی با کشیدن خطوط مختلف در تصاویر،
زمان زیادی را صرف انطباق مجموعه گاوها و مجموعه مرغها، یا چیزهای دیگر، میکنند،
این تقصیر فرگه است. برخی از کارشناسان آموزش و پرورش امیدوار بودند (و هنوز هم
ممکن است امیدوار باشند) که چنین رویکردی ممکن است درک کودکان از اعداد را بهتر کند.
فرگه به
این نتیجه رسید که تطبیق دادن کلاسها با استفاده از تناظر، در قلب چیزی نهفته است
که ما آن را ’عدد‘ میدانیم. شمارش اینکه یک کلاس چه تعدادی از چیزها را در
بردارد، تنها باعث میشود آن کلاس با کلاس استانداردی تطبیق داده شود، که مثلاً
اگر شما از فرهنگی میآیید که از حروف لاتین استفاده میکنید، اعضای آن را
علامتهای 1, 2, 3, 4, 5, 6, 7, … تشکیل میدهند. ولی فرگه
معتقد نبود مفهوم عدد باید به فرهنگ خاصی بستگی داشته باشد، بنابراین او روشی را
ابداع کرد که ما را از قید این علامتها خلاص میکرد. به معنای دقیقتر، او یک اَبر-نماد (super-symbol)
را اختراع کرد که در تمام فرهنگها یکسان بود. ولی این چیزی نبود که بتوان آن را
نوشت، بلکه کاملاً ذهنی بود.
او به این
موضوع اشاره کرد که اعضای یک کلاس خودشان میتوانند کلاس باشند. چنین چیزی اجباری
نیست، ولی چیزی هم مانع آن نمیشود. یک نمونه ساده آن، جعبه حاوی کنسرو لوبیا است:
محتویات جعبه را قوطیهای کنسرو تشکیل میدهد، و محتویات این قوطیها نیز لوبیا
هستند. بنابراین درست است که بتوان از کلاسها بعنوان اعضای کلاسهای دیگر استفاده
کرد.
اگر از
تناظر استفاده کنیم، عدد ’هفت‘ به هر کلاسی وابسته است که بتوان آن را با کلاس
فنجانها ما یا به کلاس نعلبکیهای ما، یا به کلاسی که از علامتهای 1,
2, 3, 4, 5, 6, 7 تشکیل شده است وابسته کرد. انتخاب کلاس بخصوصی از میان
اینها، و نامیدن آن بعنوان عدد هفت، یک تصمیم اختیاری است، که ظرافت خاصی ندارد و
قابل قبول هم بنظر نمیرسد. پس چرا تا آخر نرویم و از کلیه این کلاسها استفاده
نکنیم؟ آنگاه میتوان ’هفت‘ را بعنوان کلاسی از تمام کلاسهایی تعریف کرد که با هر
یک از این کلاسها (به عبارتی با همه آنها) متناظر باشد. اگر چنین کاری را انجام
دهیم، ما با بررسی اینکه آیا یک کلاسِ مفروض عضوی از این کلاسها است، میتوانیم
بگوییم که آیا آن کلاس دارای هفت عضو هست یا نه. برای راحتی کار، ما بر روی چنین
کلاسی از کلاسها برچسب ’هفت‘ را میگذاریم. ولی حتی اگر این کار را هم نکنیم، خود
کلاس گویا است. بنابراین فرگه یک عدد را از هر نام (یا نماد) اختیاری که برای آن
عدد در نظر گرفته میشود متمایز میکند.
پس از آن
او میتوانست تعریف کند که یک عدد چیست: یک عدد کلاسی از تمام کلاسهایی است که با
یک کلاس داده شده (و در نتیجه با بقیه کلاسها) متناظر باشد. منظور من هم از
’ابر-نماد‘ همین کلاس است. اگر شما به اینگونه فکر کردن تمایل دارید، این یک ایده
بسیار عالی است. در واقع بجای اینکه برای اعداد نامی را انتخاب کنیم، از نظر ذهنی
ما همه نامهای ممکن را یکجا در یک شیء واحد جمع میکنیم و بجای عدد از آن استفاده
میکنیم.
متوجه
شدید؟ بعداً در فصل [À0]
مطالب بیشتری را در اینمورد خواهید دید.
در میان
اعداد، ملموسترین آنها اعداد صحیح بین 1 تا 10
هستند.
هر کدام
از آنها منحصربفردند، و ویژگیهایی دارند که آنها را به چیز بخصوصی مبدل میکند.
درک این
ویژگیهای خاص باعث میشود تا اعداد، ملموس، دوستداشتنی، و در جای خود جالب
بنظر برسند.
بزودی شما
یک ریاضیدان خواهید شد.
کوچکترین
عدد صحیح مثبت 1 است. این عدد واحد بخش ناپذیر حساب است. این عدد تنها عددی
است که نمیتواند با جمع کردن دو عدد مثبت کوچکتر از خودش با یکدیگر حاصل شود.
1 عددی است که ما شمردن
را با آن آغاز میکنیم. با داشتن هر عددی، با اضافه کردن 1 به آن، ما عدد بعدی
را میگیریم:
2= 1 + 1
3= (1 + 1) + 1
4= ((1 + 1) + 1) + 1
... و
غیره. پرانتزها نشان دهنده عملیاتی است که باید اول صورت گیرند. ما معمولاً چنین
چیزی را از قلم میاندازیم، زیرا در اینمورد معلوم شده که ترتیب انجام کارها مهم
نیست، ولی بهتر است حواسمان از ابتدا جمع باشد.
با توجه
به این تعاریف و اصولِ قواعدِ جبر، که در یک توسعه منطقی و صوری باید بصورت صریح
بیان شوند، ما حتی میتوانیم قضیه مشهور ’2+2=4‘
(یا همان دو دوتا چهارتای خودمان) را ثابت کنیم. این اثبات بر روی یک خط جای میگیرد:
2+2=(1+1)+(1+1)=((1+1)+1)+1=4
هنگامی که
در قرن بیستم برخی از ریاضیدانان سعی میکردند اصول ریاضیات را بر مبنای یک منطقِ
استوار بنا کنند، آنها نیز از همین ایده استفاده کردند، ولی بنا به دلایل فنی،
آنها بجای 1، کار را از 0 شروع کردند [به فصل 0 رجوع کنید].
عدد 1
ایده ریاضی مهمی را بیان میکند، و آن یکتایی (uniqueness)
است. یک شیء ریاضی که ویژگی خاصی دارد، تنها وقتی یکتا است که فقط یک شیء
دارای آن ویژگی باشد. برای مثال، 2 از این جهت
یکتا است که تنها عدد اول زوج است. یکتایی به این دلیل مهم است چون به ما اجازه میدهد
ثابت کنیم که برخی از اشیاء مرموز ریاضی دراقع همان هستند که ما قبلاً درباره آنها
میدانستیم. برای مثال، اگر ما بتوانیم ثابت کنیم که یک عدد مثبت مجهول بنام n وجود دارد که هم زوج
است و هم اول، بنابراین n باید 2 باشد. بعنوان یک مثال پیچیدهتر، میتوانیم به دوازدهوجهی (dodecahedron)
اشاره کنیم که یگانه شکل چندوجهی است که دارای سطوح پنجضلعی میباشد [به فصل 5 رجوع کنید]. بنابراین اگر در یک مقاله یا کتاب ریاضی
ما به یک چندضلعی منظم برخورد کردیم که دارای سطوح پنجضلعی بود، ما یکباره، و بدون
اینکه هیچ کار دیگری انجام دهیم، میدانیم که این شکل باید دوازدهوجهی باشد. پس
از آن بقیه خواص یک دوازدهوجهی بطور رایگان بدست خواهد آمد.
هیچ کس
تابحال از سختی یاد گرفتن جدول ضرب عدد 1 شکایت نکره. ”یک یکی میشود یک، یک دوتا میشود دو،
یک سهتا میشود سه، ...“ اگر هر عددی در 1 ضرب، یا بر آن تقسیم
شود، حاصل با خود آن عدد برابر خواهد بود.
n61 ¼ n
n71 ¼ n
این تنها
عددی است که به این شیوه رفتار میکند.
در نتیجه،
1 با مربع، مکعب، و کلیه توانهای بالاتر از خودش برابر
است:
12 ¼ 161 ¼ 1
13 ¼ 16161
¼ 1
14 ¼ 1616161 ¼ 1
... و
غیره. تنها عدد دیگری که چنین خاصیتی دارد 0 است.
بهمین
دلیل، معمولاً وقتی در جبر عدد 1 بعنوان ضریب در فرمول
میآید، ما
آن را از قلم میاندازیم. برای مثال، بجای اینکه بنویسیم 1x2 þ 3x þ 4 ، تنها به نوشتن x2 þ 3x þ 4
بسنده میکنیم. تنها عدد دیگری که با
آن اینطور رفتار میکنیم 0 است، که در اینصورت
چیزی شدیدتر اتفاق میافتاد، یعنی مثلاً بجای اینکه عبارت 0x2 þ 3x þ
4 را بنویسیم، ما تنها مینویسیم 3x þ
4 و کلاً 0x2 را از
قلم میاندازیم.
...........................................
برای مطالعه ادامه این فصل نسخه کامل PDF کتاب را تهیه کنید.
اعداد زوج
بر 2 بخشپذیرند، ولی اعداد فرد اینطور نیستند. بنابراین 2
تنها عدد اول زوج است. این عدد با مجموع دو مربع برابر است: 2
¼ 12 + 12.
اعداد دیگری که چنین خاصیتی دارند، دقیقاً آنهایی هستند که وقتی بر 4 تقسیم میشوند باقیمانده آنها یک است. اعدادی که بصورت مجموع دو مربع
هستند میتوانند بصورت عوامل اول آنها مشخص شوند.
محاسبات باینری (Binary)
که در کامپیوترها انجام میشود، بجای استفاده از مبنای 10، بر مبنای توانهای 2 عمل میکند. معادلات درجه دوم (Quadratic equations)
شامل مجهولاتی با توان دو هستند، و میتوانند با استفاده از جذر گرفتن (ریشه دوم
گرفتن) حل شوند.
تمایز
میان زوج و فرد به جايگشتهای (permutation)
مختلفِ چیدن اشیاء نیز گسترش مییابد. نیمی از جايگشتها زوج، و نیمی دیگر فرد
هستند. در اینمورد من مثال سادهای را برای شما مطرح میکنم که ثابت میکند یک
معمای معروف را نمیتوان حل کرد.
یکی از
مهمترین تمایزها در کل ریاضیات، تمایز میان اعداد زوج و فرد است.
بیایید
کار خود را با اعداد صحیح 0, 1, 2, 3,… شروع کنیم. در این میان، اعداد زوج اینها هستند:
0 2
4 6 8 10 12 14 16 18 20 ...
و به همین
ترتیب اعداد فرد:
1 3
5 7 9 11 13 15 17 19 21 ...
بصورت کلی، هر عدد صحیحی که مضربی از 2 باشد زوج است، و هر عدد صحیحی که مضربی از 2 نباشد فرد است.
برخلاف آنچه برخی از معلمان تصور میکنند، 0 یک عدد زوج است، زیرا
مضربی از 2 است و میتوان آن را بصورت 062
نوشت.
شکل 8. اعداد زوج و فرد.
هنگامی که
اعداد فرد بر 2 تقسیم شوند، باقیمانده 1 خواهد بود. بنابراین
میتوان اعداد زوج را از نظر جبری بصورت 2n
نوشت که در آن n یک عدد صحیح است. به همین شکل، هر عدد فرد را میتوان بصورت 2n+1
نوشت. (در اینجا نیز اگر n=0 باشد، این نشان میدهد که 0 زوج است). برای تعمیم مفهوم ’زوج‘ و ’فرد‘ به اعداد منفی، ما اجازه میدهیم n منفی باشد. در این
صورت اعداد -2, -4, -6, … زوج و اعداد -1,
-3, -5, … فرد هستند. اعداد زوج و فرد در طول محور اعداد بصورت یک
در میان تکرار میشوند.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
کوچکترین
عدد اول فرد 3 است. معادله درجه سه شامل توان سوم (مکعب) یک مجهول
است، و میتواند با استفاده از ریشه سوم و دوم گرفتن حل شود. فضا دارای 3 بُعد است. تثلیث زاویه (یعنی سه قسمت کردن آن) با استفاده از خطکش و
پرگار غیرمدرج غیر ممکن است. دقیقاً 3 چندضلعی منظم میتوانند
صفحه را فرش کنند. هفت هشتم تمام اعداد مجموع سه مکعب هستند.
کوچکترین
عدد اول 2 است، که زوج میباشد. بعدی 3 است که کوچکترین عدد فرد اول میباشد.
بدلیل اینکه 3k بر 3 قابل قسمت است، بقیه
اعداد اول یا بصورت 3k+1 یا 3k+2
هستند، که در آن k یک عدد صحیح است. ولی گفتنیهای جالب بیشتری نیز درباره 3
وجود دارد. من صحبت درباره اعداد اول را به فصل [7] موکول میکنم.
یکی از
بزرگترین دستآوردهای ریاضیات در دوران رونسانس ایتالیا کشف چگونگی حل معادلات
درجه سوم توسط فرمولی بود که شامل ریشه سوم گرفتن و جذر گرفتن بود.
رونسانس
دورهای بود برای تحولات فکری و اختراعات جدید. ریاضیدانان آن دوره نیز از این
قاعده مستثنی نبودند، و مصمم بودند تا بر محدودیتهای ریاضیات سنتی غلبه کنند.
اولین پیشرفت بزرگ در این مسیر، یافتن روشی برای حل معادلات درجه سوم بود. نسخههای
مختلفی از این روش توسط ریاضیدانان مختلف ابداع شدند، روشهایی که آنها از چشم
دیگران پنهان نگاه میداشتند. سرانجام جرولامو کاردانو (Girolamo
Cardano)، که به جروم کاردان (Jerome
Cardan) نیز شناخته میشد، یکی از این روشها را در یک کتاب
جبر بنام هنر والا (Ars Magna) چاپ کرد. هنگامی که
وی اینکار را انجام داد، یکی دیگر از کسانی که در حل معادلات درجه سوم دست داشت او
را به دزدی اسرارش متهم کرد. چنین چیزی بعید هم نبود. کاردانو حوالی سالهای 1520
ورشکسته شده بود. پس از آن برای کسب درآمد به قمار روی آورده بود، و برای بالاتر
بردن شانس برنده شدن، از تواناییهای ریاضی خودش سود میبرد. کاردانو نابغه بود،
ولی آدم نامردی نیز بود. اما همانطور که خواهیم دید، او برای اینکار بهانههای
قابل قبولی هم داشت.
واقعه از
این قرار بود: در سال 1535 آنتونیو فیور (Antonio Fior)
و نیکولو فونتانا (معروف به تارتاگلیا Tartaglia) درگیر یک مسابقه عمومی شدند.
آنها برای یکدیگر یک معادله درجه سوم طرح کردند در این رقابتها، تارتاگلیا بطور
فراگیری فیور را شکست داد. بدلیل اینکه در آن زمان اعداد منفی هنوز شناخته نشده
بودند، معادلات درجه سوم را به سه نوع مختلف طبقه بندی کرده بودند. فیور تنها با
حلِ یک نوع از آنها آشنا بود. در ابتدا تارتاگلیا نیز فقط روش حل کردن یک نوع از
این معادلات را میدانست، ولی کمی پیش از پایان مسابقه او فهمید که چگونه انواع
دیگر را نیز حل کند.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
چند موردی
که میتوان درباره عدد چهار بیان کرد اینها هستند: اولین مربع کامل (پس از 0
و 1) عدد 4 است. در صفحه
هر نقشه را میتوان تنها با 4 رنگ رنگآمیزی کرد،
بطوری که نواحی اطراف آن رنگهای متمایزی داشته باشند. هر عدد مثبت صحیح حاصل جمع 4
مربع است. همین مورد برای مکعبها نیز حدس زده میشود، که میتواند شامل اعداد
صحیح منفی نیز بشود. معادلات درجه چهارم، که شامل توان چهارم مجهول هستند، میتوانند
با استفاده از ریشه سوم گرفتن، و جذر گرفتن حل شوند. (ریشه چهارم گرفتن معادل است
با دوبار جذر گرفتن). دستگاه اعداد چهارگانی یا کواترنیونها (quaternions)،
که بر پایه سه کمیت مستقل هستند، تقریباً از تمام قواعد استاندارد جبر
پیروی میکنند. آیا بعد چهارمی نیز میتواند وجود داشته باشند؟
عدد چهار،
یعنی 4= 2×2، یک مربع است [به فصل 2 رجوع کنید]. مربعها در کُل ریاضیات نقش مرکزی بازی
میکنند. قضیه فیثاغورث میگوید که مربعِ بزرگترین ضلع یک مثلث قائمالزاویه با
مجموع مربعات دو ضلع دیگر برابر است، بنابراین مربعها بطور ویژه در هندسه مهم
هستند.
مربعها
الگوهای پنهان زیادی را در خود دارند. برای نمونه به تفاضل میان چند مربع
متوالی توجه کنید:
1-0=1
4-1=3
9-4=5
16-9=7
اینها چه
اعداد هستند؟ اینها اعداد فرد هستند:
1 3 5 7 9
الگوی
جالب دیگری که برآیند الگوی فوق است:
1=1
1+3=4
1+3+5=9
1+3+5+7=16
1+3+5+7+9=25
اگر ما
تمام اعداد فرد را تا حد معینی با هم جمع کنیم، حاصل یک مربع است.
روشی برای درک اینکه چرا این دو مورد صحیح هستند و
چگونه با یکدیگر رابطه دارند، وجود دارد که برای آن از نقطهها استفاده میشود
(شکل سمت چپ). البته برای اثبات اینها میتوان از جبر نیز استفاده کرد:
شکل 23. چپ: 1+3+5+7+9. راست: 1+
2+ 3+ 4 +5 + 4 + 5 + 3 + 2+ 1
الگوی
جالب دیگری برای مربعها:
1=1
1+2+1=4
1 + 2 + 3 + 2 + 1 = 9
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16
1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25
این در
شکل سمت راست بصورت نقطهای نشان داده شده است.
در حدود
150 سال قبل، تعدادی از ریاضیدانان شروع به فکر درمورد نقشههای جغرافیایی کردند.
البته آنچه آنها به آن علاقه داشتند درست کردن نقشههای دقیق یا چاپ آنها بر روی
کره نبود، بلکه یک سؤال مبهم درباره خود نقشهها بود. به ویژه اینکه چطور میتوان
نواحی موجود در نقشه را رنگآمیزی کرد طوری که نواحی که با یکدیگر مرز مشترک
دارند، دارای رنگهای مختلفی باشند.
برخی از
نقشهها به رنگ زیادی نیاز ندارند. مثلاً خانههای یک صفحه شطرنج نیز مانند یک
نقشه است، با این تفاوت که صفحه شطرنج یک نقشه کاملاً منظم است. همانطور که میدانید
برای رنگآمیزی خانههای شطرنج تنها دورنگ کافی است، یکی سیاه و دیگری سفید. نقشههایی
هم که بصورت دایرههای تو در تو هستند، تنها به دو رنگ نیاز دارند. ولی هنگامی که
نواحی مختلف نظم کمتری داشته باشند، برای رنگ آمیزی آنها تنها دو رنگ کافی نیست.
برای نمونه، در زیر نقشه ایالات متحده آمریکا را
مشاهده میکنید که نواحی مختلف آن از 50 ایالت تشکیل شده است. واضح است که ما برای
متمایز نشان دادن این 50 ایالت میتوانیم از 50 رنگ مختلف استفاده کنیم. ولی روش
سادهتری هم برای اینکار هست. در اینجا خودتان سعی کنید نواحی مختلف را رنگ کنید،
بصورتی که از کمترین رنگ استفاده شود. در اینجا لازم است موضوعی را روشن میکنم:
برای رنگآمیزی ایالتهایی که فقط در یک نقطه مشترک هستند، مثل Colorado و Arizona[6]، میتوان از یک رنگ
استفاده کرد، زیرا آنها مرز مشترکی ندارند.
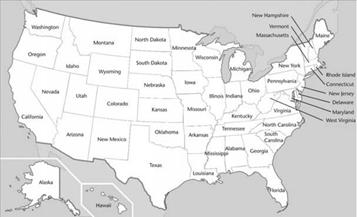
شکل 24. پنجاه ایالت مختلف امریکا بر روی نقشه.
نقشه
آمریکا چند اصل ساده را به ما نشان میدهد. ایالتهای مثل Alaska و Hawaii
حقیقتاً نقشی در این مسئله ندارند، زیرا از بقیه ایالتها جدا هستند: بنابراین میتوانیم
هر رنگی که میخواهیم به آنها بدهیم.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
مثلثهای
فیثاغورثی دارای یک زاویه قائمه، و اضلاعی با طول صحیح هستند. سادهترین آنها
دارای وتری با طول 5 و اضلاعی به طول 3
و 4 است. رویهم رفته، پنج چندوجهی (polyhedron)
منظم وجود دارد. معادله درجه پنجم، که شامل توان پنجم مجهول است، نمیتواند
بوسیله ریشه پنجم گرفتن (یا گرفتن هر ریشه دیگری) حل شود. شبکهها (Lattices)
در صفحه، و همچنین در فضای سه-بعدی، دارای تقارنهای چرخشی 5-لایه نیستند،
بنابراین چنین تقارنهایی در بلورها (crystals)
رخ نمیدهد. ولی این تقارنها میتوانند برای شبکههایی که در فضای چهار-بعدی، و
یا آنهایی که در ساختارهای عجیبی بنام شبهبلور (quasicrystals)
هستند روی دهند.
قضیه
فیثاغورث به ما میگوید که رابطه بزرگترین ضلع یک مثلث قائمالزاویه، که وتر (hypotenuse)
نام دارد، با دو ضلع دیگر در یک رابطه زیبا و ساده خلاصه میشود: مربع وتر
برابر است با مجموع مربعات دو ضلع دیگر.
این قضیه بطور سنتی به ’قضیه فیثاغورث‘
معروف شده، ولی تاریخچه آن مبهم است. لوحهای گِلی بر این دلالت دارند که بابلیان
باستان خیلی پیشتر از اینکه فیثاغورث متولد شود از این قضیه مطلع بودهاند.
احتمالاً دلیل اینکه این قضیه به فیثاغورث نسبت داده شده این دلیل است که وی
بنیانگذار یک فرقه ریاضی بود، که ’ فیثاغورثیان‘ (Pythagoreans)
نام داشت. فیثاغورثیان بر این
باور بودند که جهان بر اساس الگوهای عددی بنا شده. نویسندگان باستان قضایای ریاضی
متعددی را به فیثاغورثیان، و تا حدی به خود فیثاغورث، نسبت میدادند، ولی ما هیچ
مدرکی دردست نداریم که کدام یک از آنها از خود فیثاغورث سرچشمه گرفته. ما حتی نمیدانیم
که آیا این فیثاغورثیان بودند که قضیه فیثاغورث را اثبات کردند، و یا آنها تنها به
صحت آن اعتقاد داشتند.
اولین
اثبات شناخته شده قضیه فیثاغورث ابتدا در کتاب اصول (Elements)
اقلیدس آمده بود. این اثبات کمی پیچیده بود، و شامل شکلی بود که دانشآموزان قرن
نوزدهمی نام ’ شورت
اقلیدس‘ را بر روی آن
گذاشته بودند، زیرا شبیه یک شورت مردانه بود. تقریباً صدها اثبات برای قضیه
فیثاقورث ارائه شده.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
کوچکترین
عددی که با مجموع مقسومعلیههای واقعی خودش برابر است عدد شش است: 6= 1
+ 2 + 3. عدد مماسی در صفحه 6 است. شانههای عسل
بصورت ششضلعی تشکیل میشوند. دقیقاً 6 چندبر (polytopes) چهار-بعدی وجود
دارند.
یونانیان
باستان اعداد صحیح را برحسب مقسومعلیههای آنها به سه گونه تقسیم میکردند:
· اعداد زائد (Abundant
numbers)، که مجموع مقسومعلیههای واقعی آنها (یعنی مقسومعلیهها
به غیر از خود عدد) بزرگتر از عدد است.
· اعداد ناقص (Deficient numbers)، که مجموع مقسومعلیههای واقعی آنها کوچکتر از عدد
است.
· اعداد تام (Perfect numbers)، که مجموع مقسومعلیههای واقعی آنها برابر با عدد
است.
چند عدد
از این نوع را در جدول 7 میبینید.
این نشان میدهد که هر سه گونه از این اعداد وجود
دارند، ولی همچنین نشان دهنده این است که تعداد اعداد ناقص بیشتر از دو گونه دیگر
هستند. در سال 1998 مارک دِلِگلیز (Marc
Deléglise) ثابت کرد که اگر عدد n به اندازه کافی بزرگ انتخاب شود، نسبت اعداد
ناقص میان 1 تا n
به سمت ثابتی میان 0.7520 و 0.7526
میل میکند، درحالی که نسبت اعداد زائد میان 0.2474
و 0.2480 است. قبلاً در سال 1955 هانس-یواخیم کانولد (Hans-Joachim Kanold)
ثابت کرده بود که نسبت اعداد کامل به سمت 0 میل میکند. بنابراین
تقریباً سه چهارم اعداد صحیح ناقص، و یک چهارم بقیه زائد هستند، و به سختی میتوان
اعداد تام را میان آنها پیدا کرد.
|
عدد |
مجموع مقسومعلیههای واقعی |
گونه |
|
1 |
0 |
ناقص |
|
2 |
1 |
ناقص |
|
3 |
1 |
ناقص |
|
4 |
1+2=3 |
ناقص |
|
5 |
1 |
ناقص |
|
6 |
1+2+3=6 |
تام |
|
7 |
1 |
ناقص |
|
8 |
1 + 2 + 4 = 7 |
ناقص |
|
9 |
1+3=4 |
ناقص |
|
10 |
1+2+5=8 |
ناقص |
|
11 |
1 |
ناقص |
|
12 |
1+2+3+4+6=16 |
زائد |
|
13 |
1 |
ناقص |
|
14 |
1+7=8 |
ناقص |
|
15 |
1+3+5=8 |
ناقص |
جدول 7
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
چهارمین
عدد اول 7 است، و این فصل جای مناسبی است که توضیح
دهیم کاربرد اعداد اول چیست و چرا آنها جالب هستند. در بسیاری از مسائلی که اعداد
صحیح در هم ضرب میشوند سر و کله اعداد اول پیدا میشود. آنها ’اجزاء سازنده‘ همه
اعداد صحیح هستند. ما در فصل 1 دیدیم که تمام اعداد
صحیح بزرگتر از 1، یا اول هستند یا میتوانند از ضرب دو یا چند عدد اول
در یکدیگر حاصل شوند.
عدد 7
همچنین پیوندهایی با مسئله قدیمی و حل نشده فاکتوریلها (factorials)
دارد. این عدد همچنین نشان دهنده کمترین تعداد رنگهایی است که میتوان برروی یک چنبره (torus)
نقشههایی را کشید، بصورتی که مناطق مجاور دارای رنگهای متفاوتی باشند.
گاوس، که
یکی از برجستهترین متخصصان نظریه اعداد در عصر خود و یکی از بزرگترین ریاضیدانان
تمام اعصار بود، در سال 1801 کتاب پیشرفتهای درباره نظریه اعداد منتشر کرد که نام
آن تحقیقات حسابی بود. در میان موضوعات پیشرفته، او به این اشاره کرد که دو
موضوع هستند که بسیار اهمیت دارند: ’مسئله تمایز بین اعداد اول و اعداد مرکب، و
همچنین تجزیه اعداد مرکب به عوامل اول، مهمترین و پرکاربردترین مسائل در حساب
هستند.‘
روشنترین
روش برای حل کردن این دو مسئله این است که همه عوامل را امتحان کرد. مثلاً، اگر میخواهیم
ببینیم که آیا 35 اول است یا نه، و اگر اول نیست عوامل اول آن را پیدا
کنیم، در اینصورت مانند زیر عمل میکنیم:
35÷2 = 17 (با باقیمانده 1)
35÷3 = 11 (با باقیمانده 2)
35÷4 = 8 (با باقیمانده 3)
35÷5 = 7 (بدون باقیمانده)
بنابراین 35=5
× 7، و چون ما 7 را به عنوان یک عدد
اول میشناسیم، بنابراین تجزیه 35 کامل شده.
میتوان
این روند را کمی سادهتر کرد. اگر ما از قبل فهرستی از اعداد اول را داشته باشیم، تنها
نیاز داریم که این اعداد را بعنوان مقسومعلیه امتحان کنیم. برای نمونه، با دانستن
اینکه 2 نمیتواند مقسومی برای 35
باشد، ما میدانیم که 4 هم نمیتواند این عدد
را تقسیم کند. دلیلش هم این است که 2 میتواند 4
را تقسیم کند، بنابراین هر چیزی که بر 4 بخشپذیر باشد، 2
نیز آن را تقسیم میکند. (همین برای 6، 8،
و یا هر عدد زوج دیگری نیز صادق است).
ما همچنین
میتوانیم وقتی به جذر عدد مورد نظر رسیدیم، کار تقسیم را متوقف کنیم. چرا؟ برای
روشنتر شدن موضوع، عدد 4283 را درنظر بگیرید که
جذر آن تقریباً برابر است با 65.44. اگر ما دو عدد را که
از این مقدار بزرگتر باشند درهم ضرب کنیم، حاصل آن از 4283، بزرگتر میشود.
بنابراین ما 4283 را به دو (یا چند) عامل تقسیم میکنیم، که حداقل یکی از
آنها کمتر یا مساوی جذر آن باشد. در واقع اگر ما در هنگام جذر گرفتن قسمت اعشاری
را کنار بگذاریم و فقط قسمت صحیح را درنظر بگیریم، این عدد باید کمتر یا برابر 65
باشد.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
عدد 8
اولین مکعب غیربدیهی (nontrivial) است. 8 یک عدد فیبوناچی (Fibonacci)
نیز هست. آیا مکعبهای
فیبوناچی دیگری نیز وجود دارند؟ فکر کردن در مورد مکعبها، فرما را بر آن داشت که
آخرین قضیه مشهور خود را ارائه دهد. یکی از برجستهترین ریاضیدانان زن تاریخ بنام سوفی ژرمن (Sophie
Germain)، در یک مورد خاصِ این قضیه سهم زیادی دارد. سرانجام
350 سال بعد از حدس اولیه فرما، اندرو وایلز (Andrew Wiles)
توانست این قضیه را اثبات کند.
مکعب یک
عدد با سه بار ضرب کردن آن عدد در خودش حاصل میشود. برای نمونه، مکعب 2 عبارت است از 2 × 2 × 2=8. مکعب عدد n
بشکل n3
نوشته میشود. چند مکعب اعداد نخست بصورت زیر هستند:
n: 0 1
2 3
4 5
6 7
8 9 10
n3: 0 1
8 27 64 125
216 343 512 729 1000
مکعبها
باعث بوجود آمد یک سری از ایدهها شد که بیش از 300 سال قدمت دارند.
در حوالی
سال 1630، فرما متوجه شد که از جمع کردن دو مکعب با یکدیگر، نمیتوان هیچ عدد مکعب
دیگری را حاصل کرد (البته اگر صفر را وارد کنیم، این مسئله به یک چیز بدیهی تبدیل
میشود، زیرا برای هر عددی مانند n،
03+n3=n3 همیشه درست است). او در سال 1621 شروع به خواندن کتاب جبر معروف دیوفانتوس
بنام حساب (Arithmetica) کرد. همانطور که او
این کتاب را میخواند، در حاشیه آن یادداشتی را نوشت: ’این غیر ممکن است که بتوان
یک مکعب را به دو مکعب، یا یک توانِ چهارم را به دو توان چهارم، یا در کل هر توانی
به غیر از دو را به دو توان از همان نوع تقسیم کرد. من اثبات جالبی برای این مسئله
پیدا کردهام، ولی حاشیه این کتاب اجازه نمیدهد تا آن را در اینجا بنویسم.‘
اگر
بخواهیم به زبان جبر صحبت کنیم، فرما ادعا میکرد که ثابت کرده که اگر n
عدد صحیحی بزرگتر از 2 باشد، آنگاه معادله زیر هیچ جوابی ندارد:
xn+ yn=zn
این مسئله
بعدها به ’آخرین قضیه فرما‘ (Fermat’s last
theorem) معروف شد، که ابتدا در سال 1670 در نسخهای از کتاب
حساب دیوفانتوس دیده شد که توسط ساموئل (پسر فرما) انتشار یافت.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
کوچکترین
مربع جادویی غیربدیهی 9 خانه دارد. در صفحه به 9 روش میتوان توسط چندضلعیهای
منظم کاشیکاری کرد، به نحوی که در تمام گوشهها به همان صورت چیده شده باشند.
مستطیلی که دارای ابعاد درستی باشد میتواند به 9 مربع با اندازههای
مختلف تقسیم شود.
مربعهای جادویی
(یا مربعهای وفقی) مربعهایی هسته که از آرایهای از اعداد تشکیل شدهاند،
و معمولاً بصورت 1، 2، 3،
... تا یک عدد معین شماره گذاری شدهاند. در این مربعها حاصل جمع هر سطر، هر
ستون، و قطر با هم یکسان هستند. آنها اهمیت خاصی در ریاضیات ندارند، ولی رویهم
رفته جالبند. اگر از مربع بیمایه 1 × 1 صرفنظر کنیم، کوچکترین مربع جادویی دارای
3 × 3، یا 9 خانه است.
شکل 50. سمت چپ: LO Shu.
سمت راست: نسخه امروزی.

شکل 51. سمت چب: تصویر تَبتی لوشو. سمت راست:
امپراطور یو.
قدیمیترین
مربع جادویی شناخته شده به یک افسانه چینی قدیمی درباره امپراتور یو (Yu) مربوط میشود که
بدلیل رخ دادن یک سیل عظیم، مشغول قربانی کردن به درگاه خدای رودخانه لو (Luo) است. لاکپشتی جادویی
از رودخانه بیرون میآید، که طرح ریاضی عجیبی بر کاسه او نقش بسته. این لو شو (Lo
Shu) بود، یعنی یک مربع جادویی که بر روی یک شبکه 3 × 3 کشیده شده است، ولی در آن بجای اعداد از نقاط استفاده شده بود.
اگر در
مربع جادویی از ارقام 1 تا 9
استفاده شود، و از هر کدام فقط یکبار، آنگاه لو شو تنها چیدمان ممکن است (البته به
غیر از چرخش، و انعکاس مربع). ثابت جادویی (یعنی مجموع اعداد در سطرها، ستونها، و
قطرها) 15 است. در این مربع الگوهای دیگری نیز دیده میشود. اعداد
زوج در چهار گوشه آن قرار دارند. مجموع اعدادی که در قطرها مقابل هم قرار دارند
همیشه 10 است.
اندازه هر
مربع جادویی، رتبه آن نامیده میشود. رتبه لو شو 3 است، و هر مربعی که
رتبه آن n باشد دارای n2 خانه است، که معمولاً در آن اعدادی مابین 1
تا n2 قرار دارد.
در
فرهنگهای باستانی دیگر (مثل ایران و هند) نیز مربعهای جادویی جذابیت داشته. در
قرن دهم در معابد خاجوراهوی هند یک مربع جادویی با رتبه 4 پیدا شد، که مانند
بقیه مربعهای مرتبه 4 که در آنها از اعداد 1-16
استفاده میشود، ثابت جادویی آن 34 بود.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
دستگاه اعشاری (decimal
system) که ما برای نوشتن اعداد از آن استفاده میکنیم بر
مبنای 10 است، و احتمالاً دلیلش هم این است که دستها
و پاهای ما ده انگشت دارند. اعداد میتوانند در مبناهای دیگری نیز نوشته شوند، که
در زمانهای باستان از برخی از آنها استفاده میشده (خصوصاً مبنای 20
و 60). ده هم یک عدد مثلثی (triangular)
و هم یک عدد چهاروجهی (tetrahedral) است. برخلاف آنچه اویلر تصور میکرد،
2 مربعِ لاتینِ متعامد 10 × 10 وجود دارد.
دستگاهی
که ما امروزه از آن استفاده میکنیم ’اعشاری‘ نام دارد زیرا پایه آن عدد 10
است. در لاتین واژه دِسیم (Decem)
به معنای ده است[7]،
و به همین دلیل در زبانهای اروپایی به این دستگاه دِسیمال گفته میشود. در این دستگاه از ده علامت 0 1
2 3 4 5 6 7 8 9 برای نمایش یکها، دهها، صدها، هزارها، و
غیره استفاده میشود. برای مثال عدد 2015 به این معنی است:
5 یک
1 ده
0 صد
2 هزار
چیزی که در
اینجا نقش عمده دارد توانهای متوالی 10 است:
100=1
101=10
102=100
103=1000
ما آنقدر
به این نوع عددنویسی (notation) عادت کردهایم که
پیش خود تصور میکنیم فقط اینها عدد هستند، و فکر میکنیم عدد 10 از نظر ریاضی ویژگی خاصی دارد. ولی دستگاههای عددنویسی مشابهای را میتوان
ساخت که مبناهایی غیر از 10 داشته باشند.
بنابراین گرچه 10 از جهاتی خاص است (بعداً خواهیم دید چرا)، ولی از لحاظ
عددنویسی خاص نیست.
در
کامپیوترها از چند پایه مختلف استفاده میشود:
پایه 2:
که سیستم باینری (binary) نامیده میشود، و در آن از علامتهای 0
و 1 استفاده میشود.
پایه 8:
که سیستم اُکتال (octal)
نامیده میشود و در آن از علامتهای 0 1 2 3 4 5 6 7 استفاده میشود.
پایه 16:
که سیستم هگزادسیمال (hexadecimal)
نامیده میشود و در آن از علامتهای 0 1 2 3 4 5 6 7 8 9 A B C D E F استفاده میشود.
هر از
چندگاهی پیشنهاد میشود از سیستم دوازدهگانی (Duodecimal)
استفاده شود، که پایه آن 12 است. مزیت 12
این است که بر اعداد 2، 3، 4،
و 6 بخشپذیر است، درحالی که 10 فقط بر اعداد 2،
و 5 بخشپذیر است. مایاها (Mayans)
از پایه 20، و بابلیان باستان از پایه 60 استفاده میکردند.
ما میتوانیم
عدد 2015، که در مبنای اعشاری نوشته شده، را بصورت زیر باز کنیم:
2 × 1000 + 0 × 100 + 1 × 10 + 5 × 1
یا میتوانیم
آن را بصورت توانی بنویسیم:
2×103 + 0×102 + 1×101
+5×100
این گونه عددنویسی،
عددنویسی مکانی نامیده میشود، زیرا معنی هر رقم به مکان آن بستگی دارد.
اگر از
ارقام قبلی در مبنای 8 استفاده شود معنی آن این است:
2×83 + 0×82 + 1×81
+5×80
که مقدار
آن در مبنای اعشاری میشود:
2×512 + 0×64 + 1×8 +5×1=1037
بنابراین
ارقام یکسان، اگر در پایههای مختلف استفاده شوند، نشان دهنده اعداد مختلفی هستند.
اجازه
دهید تا پایه کمتر شناخته شده دیگری را امتحان کنیم، مثلاً 7. ساکنان یک منظومه
خیالی بنام Apellobetnees III
همه دارای هفت انگشت هستند و سعی میکنند با آنها اشیاء را بشمارند. بنابراین
دستگاه عددی آنها تنها دارای ارقام 0-6 است. آنها بجای اینکه
عدد هفت را بصورت 7 بنویسند، آن را بصورت 10
مینویسند، و تا عدد 66 ادامه میدهند (که در مبنای 10 برابر 48 است). برای نوشتن عدد بعدی (که 49 باشد)، آن را بصورت 100
مینویسند و ... به همین ترتیب.
بنابراین
عددی که در دستگاه Apellobetnees بصورت abcd
نوشته شده، به صورت زیر به دستگاه اعشاری ترجمه میشود:
a × 73 + b× 72 + c× 7 + d = 343a + 49b
+ 7c + d
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب
را تهیه کنید.
حال که
تکلیف اعداد 1-10
را مشخص کردیم، یک قدم جلو گذاشته و به معرفی 0 میپردازیم.
اگر از 0 یک قدم به عقب
برگردیم، -1 را خواهیم گرفت، و این برای ما دریچه کاملاً جدیدی
را بسوی اعداد منفی و کاربرد آنها را خواهد گشود.
دیگر از
اعداد فقط برای شمردن استفاده نمیشود.
از ابتدا
کاربرد صفر برای بهتر نوشتن اعداد بود، و فقط وسیلهای بود که برای عدد نویسی بکار
گرفته میشد. قرنها طول کشید که مستقلاً بعنوان یک عدد پذیرفته شده، و به آن
اجازه داده شود تا جایگاه خود را بعنوان یکی از ویژگیهای اصلی دستگاه اعداد بدست
آورد. ولی این عدد ویژگیهای غیرمتعارف، و تا حدی متناقضی، را در خود دارد.
مهمترین ویژگی آن این است که شما بطور معقول نمیتوانید هیچ عددی را بر 0
تقسیم کنید. در بنیانهای منطق ریاضی، کلیه اعداد را میتوان از 0
حاصل کرد.
در بسیاری
از فرهنگهای باستانی، علائمی که برای 1، 10،
و 100 از آنها استفاده میشود به یکدیگر هیچ ربطی ندارند.
برای نمونه یونانیان باستان برای نمایش اعداد 1-9 و 100-900
از حروف الفبای خود استفاده میکردند. این مسئله میتوانست بالقوه گیجکننده باشد،
هر چند معمولاً از روی زمینهِ متن بسادگی میتوان تشخیص داد که آیا علائم
نشاندهنده اعداد هستند یا حروف. ولی این باعث میشد تا انجام عملیات حسابی نیز سختتر
شود.
برای
نوشتن اعداد مختلف، ما در همه آنها از ارقام یکسانی (0-9) استفاده میکنیم، و
این جایگاه (یا مکان) ارقام است که در اعداد مختلف تغییر میکند. عدد نویسی مکانی مزیتهای عمدهای برای انجام
محاسبات دارد، مخصوصاً محاسباتی که تا همین اواخر با قلم و کاغذ انجام میگرفت. در
عدد نویسی مکانی، چیز عمدهای که برای حساب کردن به آن نیاز دارید یکی داشتن
قواعدی برای جمع و ضرب است و دیگری داشتن ده علامت 0-9. هنگامی که علائم
یکسان در مکانهای مختلف ظاهر شوند، الگوهای مشترکی ظاهر میشود. مثلاً:
23+5 ¼ 28 230+50 ¼ 280
2300+500 ¼ 2800
شکل 66.
اگر از
عدد نویسی یونانی استفاده کنیم، دو مورد فوق به صورت زیر خواهد بود:
kg +e ¼ kZ sl+n ¼ sp
که هیچ
ساختار مشترکی در آنها دیده نمیشود.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
آیا عددی
هست که از صفر کمتر باشد؟ شما نمیتوانید چنین چیزی را با درنظر گرفتن گاوها تصور کنید،
مگر اینکه نوعی از ’گاوهای مجازی‘ را وارد کار کنید که آنها را به شخص دیگری
بدهکار هستید. با این کار شما بصورت طبیعی مفهوم اعداد را گسترش دادهاید، و
همچنین زندگی را برای جبردانان و حسابدارها خیلی سادهتر میکنید. ولی شگفتیهای
خاصی هم در اینجا وجود دارد، مثلاً حاصل ضرب منفی در منفی میشود مثبت. چرا چنین
است؟
بعد از
اینکه یادگرفتیم چگونه اعداد را با هم جمع کنید، ما به فکر انجام عمل معکوس جمع،
یعنی تفریق میافتیم. برای نمونه حاصل 4-3 هرچه باشد (که البته 1
است)، وقتی با 3 جمع شود حاصل آن 4 خواهد بود. عمل تفریق
به این دلیل مفید است که به ما نشان میدهد اگر مثلاً 4 دلار داشته باشیم و 3
دلار آن را خرج کنیم، در آخر چقدر برای ما میماند.
کم کردن
یک عدد کوچکتر از یک عدد بزرگتر مشکلی ندارد. اگر ما کمتر از آنچه در جیب داریم
خرج کنیم، مشکلی نخواهیم داشت و باز هم چیزی برای ما خواهد ماند. ولی اگر ما یک
عدد بزرگتر را از یک عدد کوچکتر کم کنیم، آن وقت چطور؟ برای مثال، حاصل 3-4
چیست؟
اگر در
جیب خودتان یک اسکناس یک دلاری داشته باشید، شما نمیتوانید چهارتای آنها را از
جیب درآورید و مثلاً آنها را برای خرید چیزی به یک فروشنده بدهید. ولی این روزها
کارتهای اعتباری هستند، که شما بسادگی میتوانید پولهایی را خرج کنید که در جیبتان وجود ندارند (یا حتی پولهایی را خرج کنید
که در حساب بانکی شما نیز وجود ندارند!). وقتی چنین اتفاقی بیافتد، شما بدهکار
میشوید. در اینصورت شما یک دلار به بانک بدهکار میشوید (البته بدون احتساب
سود بدهیتان). بنابراین به یک معنا 3-4 برابر 1
است، ولی نوع دیگری از 1، یک بدهی، نه پول نقد
واقعی. اگر عدد 1 مقدار مخالفی داشته باشد، این همان مقدار است.
برای
تمایز بدهی از نقد، ما در سمت چپ آن عدد یک علامت منفی قرار میدهد. بنابراین:
3-4=-1
و به این
طریق ما عدد جدیدی را اختراع کردیم: یک عدد منفی.
از نظر
تاریخی اولین توسعه عمده دستگاه اعداد، اختراع اعداد کسری بود [به فصل ![]() رجوع کنید]. اعداد منفی در مرتبه دوم قرار میگیرند.
ولی من قصد دارم ابتدا اعداد منفی را بررسی کنم. نخستین ظهور شناخته شده اعداد
منفی در یک کتاب چینی از سلسله هان (Han)
دیده شد، که به سالهای 202 قبل از میلاد تا 220 بعد از میلاد تعلق دارد و Jiu Zhang Suan Shu نام دارد (به معنای ’نه
فصل در باب هنر ریاضی‘).
رجوع کنید]. اعداد منفی در مرتبه دوم قرار میگیرند.
ولی من قصد دارم ابتدا اعداد منفی را بررسی کنم. نخستین ظهور شناخته شده اعداد
منفی در یک کتاب چینی از سلسله هان (Han)
دیده شد، که به سالهای 202 قبل از میلاد تا 220 بعد از میلاد تعلق دارد و Jiu Zhang Suan Shu نام دارد (به معنای ’نه
فصل در باب هنر ریاضی‘).
هنگامی که
ریاضیدانان میخواستند یک عدد را بر عدد دیگری تقسیم کنند، و نتیجه دقیقی حاصل نمیشد،
آنها کسور را اختراع کردند.
هنگامی که
میخواستند یک عدد بزرگتر را از یک عدد کوچکتر کم کنند، آنها اعداد منفی را اختراع
کردند.
ریاضیدانان
هر موقع نتوانند کاری را با ابزارهای موجود انجام دهند، چیز جدیدی را اختراع میکنند
که توسط آن میتوان چنین کاری را انجام داد.
بنابراین
هنگامی که امکان یافتن جذر یک عدد منفی برای آنها دغدغه شد ... حدس بزنید چه
اتفاقی افتاد؟
من قبلاً
اشاره کردم که ما تمایل داریم اعداد را بعنوان یک چیز ثابت و تغییرناپذیر در نظر
بگیریم، ولی درواقع آنها اختراع انسان هستند. اعداد با شمردن آغاز میشود، ولی مفهوم
عدد بطور مکرر در حال گسترش بوده. اضافه شدن صفر، اعداد منفی، اعداد گویا (کسور)،
اعداد حقیقی (اعداد اعشاری نامتناهی) ... همه نمونههایی از این گسترش هستند.
باوجود
تفاوتهای فنی میان این دستگاهها، همه آنها یک حس را دارند. شما میتوانید در هر
یک از این دستگاهها محاسباتی را انجام دهید، و میتوانید دو عدد را با هم مقایسه
کنید تا ببینید کدام یک از آنها بزرگتر است. یعنی در تمام آنها مفهوم ترتیب (order)
وجود دارد. ولی از قرن پانزدهم به بعد، برخی از ریاضیدانان به این فکر افتادند که
آیا ممکن است نوع جدیدی از اعداد وجود داشته باشند که دارای خواصی باشند که کمتری
ملموسند، و مثلاً رابطه ترتیب (یعنی بزرگتر یا کوچکتر بودن) در آنها دیگر معنی
نداشته باشد.
بدلیل
اینکه منفی در منفی با مثبت برابر است، مربع هر عدد حقیقی یک عدد مثبت است.
بنابراین در حوزه اعداد حقیقی، اعداد منفی جذر ندارند. این مورد کمی ناراحتکننده
است، خصوصاً در جبر. ولی برخی نتایج عجیب در جبر، که راههایی را برای حل معادلات
فراهم آوردهاند، حاکی از این هستند که باید راهی برای معقول ساختن عباراتی نظیر ![]() وجود داشته باشد. بنابراین ریاضیدانان پس از مدتها
سرگشتگی تصمیم گرفتند تا نوع جدید از اعداد را اختراع کنند که در آنها ریشه دوم
اعداد منفی نیز موجود باشد.
وجود داشته باشد. بنابراین ریاضیدانان پس از مدتها
سرگشتگی تصمیم گرفتند تا نوع جدید از اعداد را اختراع کنند که در آنها ریشه دوم
اعداد منفی نیز موجود باشد.
مرحله
کلیدی معرفی جذر -1
است. اویلر در مقالهای که در سال
1777 به زبان فرانسه منتشر کرد، علامت i را برای نمایش ![]() معرفی کرد. بدلیل اینکه این عدد مانند اعداد ’حقیقی‘
رفتار نمیکرد، او این عدد را موهومی (imaginary)
نامید. با تعریف i،
شما باید اعدادی مثل 2+3i را نیز مجاز
بشمارید، این نوع اعداد مختلط (complex) نامیده میشوند. بنابراین شما عدد جدیدی را نخواهید
داشت، بلکه یک دستگاه اعدادِ گسترش یافته را خواهید داشت.
معرفی کرد. بدلیل اینکه این عدد مانند اعداد ’حقیقی‘
رفتار نمیکرد، او این عدد را موهومی (imaginary)
نامید. با تعریف i،
شما باید اعدادی مثل 2+3i را نیز مجاز
بشمارید، این نوع اعداد مختلط (complex) نامیده میشوند. بنابراین شما عدد جدیدی را نخواهید
داشت، بلکه یک دستگاه اعدادِ گسترش یافته را خواهید داشت.
از نظر
منطقی، اعداد مختلط به اعداد حقیقی وابسته هستند. برای روشن شدن این مسئله نیاز
است تا تاریخچه این اعداد را بررسی کنیم.
حساب و
جبر اعدادِ مختلط ساده هستند. شما از قواعد عادی برای جمع و ضرب آنها استفاده میکنید،
با این تفاوت که هر موقع به عبارت i2
برخورد کردید، باید بجای آن -1
بگذارید. برای نمونه:
(2 + 3i) + (4 –i) = (2 + 4) + (3i- i) = 6 + 2i
(2 + 3i) × (1 + i) = 2 + 2i
+ 3i + 3i × i = 2 + 5i + 3 × -1
= (2-3) + 5i=-1 + 5i
هنگامی که
پیشگامان اولیه چنین ایدههایی را کشف کردند، بنظر میرسید که آنها گونهای از
اعداد را بدست آوردهاند که از نظر منطقی استوار هستند و دستگاه اعداد حقیقی را
توسعه میدهند.
چنین چیزی
سابقه داشت. دستگاه اعداد قبلاً بارها توسعه داده شده بود. ولی اینبار، باید
مفاهیمی مثل ’بزرگتر بودن‘ کنار گذاشته شود. این مفهوم برای اعداد موجود مناسب
بود، ولی اگر میخواستید از آن برای اعداد جدید استفاده کنید با مشکل مواجه میشدید.
عجیب است، ولی اعداد مختلط اعدادی هستند که دارای اندازه نیستند! با
اینکه اعداد مختلط دستگاه اعداد حقیقی را گسترش میدهند ولی نمیتوان مفهوم اندازه
را در آنها مطرح کرد، و این مورد بقدری عجیب بود که ریاضیدانان به این فکر افتاند
که آیا چنین گسترشی مجاز است یا نه. آنها قبلاً با چنین سؤالی مواجه نشده بودند،
زیرا اعداد کسری یا منفی را میشد به جهان واقعی تشبیه کرد. ولی i یک علامت بود، و طوری
رفتار میکرد که قبلاً تصور میشد غیر ممکن است.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
حالا ما
به سمت کسور حرکت میکنیم. ریاضیدانان ترجیح میدهند برای کسور از نام زیباتری
استفاده کنند و آنها را اعداد گویا (rational
numbers) بنامند.
اینها اعدادی مثل ![]() ،
،
![]() ،
یا
،
یا ![]() ،
هستند که از تقسیم یک عدد صحیح بر عدد صحیح دیگری بدست میآیند. تصور کنید که به
روزهایی باز گردید که منظور از ’عدد‘، یک عدد کامل بود. در آن دوران وقتی عددی میتوانست
عدد دیگری را کاملاً بشمارد، تقسیم آنها نیز معقول بود، برای نمونه 4=
،
هستند که از تقسیم یک عدد صحیح بر عدد صحیح دیگری بدست میآیند. تصور کنید که به
روزهایی باز گردید که منظور از ’عدد‘، یک عدد کامل بود. در آن دوران وقتی عددی میتوانست
عدد دیگری را کاملاً بشمارد، تقسیم آنها نیز معقول بود، برای نمونه 4= ![]() .
ولی از این طریق شما چیز جدیدی را بدست نمیآوردید. کسور وقتی جالب میشوند که
تقسیم دو عدد میسر نباشد. به عبارت دقیقتر، هنگامی که حاصل تقسیم یک عدد کامل
نباشد. در اینحالت ما به نوع جدیدی از اعداد نیاز داریم.
.
ولی از این طریق شما چیز جدیدی را بدست نمیآوردید. کسور وقتی جالب میشوند که
تقسیم دو عدد میسر نباشد. به عبارت دقیقتر، هنگامی که حاصل تقسیم یک عدد کامل
نباشد. در اینحالت ما به نوع جدیدی از اعداد نیاز داریم.
سادهترین
کسر، و همان که در زندگی روزمره از آن بسیار استفاده میکنیم، کسر نیمه (نصفه)، یا
همان ![]() است. ما بطور گسترده در زندگی روزمره از نیمهها
استفاده میکنیم: نصف پیمانه شیر، دو نیمه مسابقه فوتبال، بلیط نیم بها، نیم ساعت،
... و غیره. گرچه
است. ما بطور گسترده در زندگی روزمره از نیمهها
استفاده میکنیم: نصف پیمانه شیر، دو نیمه مسابقه فوتبال، بلیط نیم بها، نیم ساعت،
... و غیره. گرچه ![]() سادهترین کسر است، ولی میتوان گفت مهمترین آنها
نیز محسوب میشود. اقلیدس میدانست که چگونه خطوط و زویا را به دو قسمت تقسیم کند،
به عبارتی، چگونه آنها را نصف کند. ویژگی دیگری که کمی پیشرفتهتر است، در نظریه
تحلیلی اعداد ظاهر میشود: حدس زده میشود که جوابهای غیربدیهی تابع زتای ریمان (Riemann
zeta function) همیشه دارای جزء حقیقی
سادهترین کسر است، ولی میتوان گفت مهمترین آنها
نیز محسوب میشود. اقلیدس میدانست که چگونه خطوط و زویا را به دو قسمت تقسیم کند،
به عبارتی، چگونه آنها را نصف کند. ویژگی دیگری که کمی پیشرفتهتر است، در نظریه
تحلیلی اعداد ظاهر میشود: حدس زده میشود که جوابهای غیربدیهی تابع زتای ریمان (Riemann
zeta function) همیشه دارای جزء حقیقی ![]() باشند. احتمالاً این مهمترین مسئله در تمام ریاضیات است
که هنوز حل نشده باقی مانده.
باشند. احتمالاً این مهمترین مسئله در تمام ریاضیات است
که هنوز حل نشده باقی مانده.
طبیعت خاص ![]() خیلی زود خودش را در هندسه اقلیدسی نشان داد. در جلد
اول کتاب اصول اقلیدس، ترسیمی برای ’نصف کردن یک زاویه‘ نشان داده شده،
یعنی اینکه چگونه میتوان یک زاویه مفروض را نصف کرد. چگونگی آن از این قرار است:
زاویهای مانند BAC داده شده، با استفاده از یک پرگار نقاط D و E را به فاصلههای یکسان از A بر روی خطوط AB و AC رسم کنید. حالا در نقطه D کمانی به شعاع DE و کمان دیگری به مرکز E و به شعاع ED رسم کنید. آنها
در نقطه بنام F
که از D و E به یک فاصله است همدیگر را
قطع میکنند. حالا خط AF
زاویه BAC را نصف میکند. در
واقع اقلیدس مرحله آخر را طور دیگری
شرح میدهد: مثلث متساویالاضلاع DEF
را رسم کنید. این یک تصمیم ماهرانه است که او بر اساس آنچه قبلاً اثبات کرده بود
گرفت، و بدلیل اینکه مثلث DEF متساویالاضلاع
است، دقیقاً همان نتیجه را میدهد.
خیلی زود خودش را در هندسه اقلیدسی نشان داد. در جلد
اول کتاب اصول اقلیدس، ترسیمی برای ’نصف کردن یک زاویه‘ نشان داده شده،
یعنی اینکه چگونه میتوان یک زاویه مفروض را نصف کرد. چگونگی آن از این قرار است:
زاویهای مانند BAC داده شده، با استفاده از یک پرگار نقاط D و E را به فاصلههای یکسان از A بر روی خطوط AB و AC رسم کنید. حالا در نقطه D کمانی به شعاع DE و کمان دیگری به مرکز E و به شعاع ED رسم کنید. آنها
در نقطه بنام F
که از D و E به یک فاصله است همدیگر را
قطع میکنند. حالا خط AF
زاویه BAC را نصف میکند. در
واقع اقلیدس مرحله آخر را طور دیگری
شرح میدهد: مثلث متساویالاضلاع DEF
را رسم کنید. این یک تصمیم ماهرانه است که او بر اساس آنچه قبلاً اثبات کرده بود
گرفت، و بدلیل اینکه مثلث DEF متساویالاضلاع
است، دقیقاً همان نتیجه را میدهد.
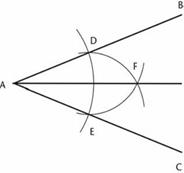
شکل 76. چگونگی نصف کردن یک زاویه.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
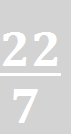
در بسیاری
از کتابهای درسی ابتدایی به ما گفته میشود که ’ ![]() =π‘. ولی آیا واقعاً ما میتوانیم
این تساوی را جدی بگیریم؟ حتی اگر خطای این کسر کوچک باشد، اصلاً از کجا آمده؟
=π‘. ولی آیا واقعاً ما میتوانیم
این تساوی را جدی بگیریم؟ حتی اگر خطای این کسر کوچک باشد، اصلاً از کجا آمده؟
عدد π نمیتواند دقیقاً با ![]() برابر باشد، زیرا π یک عدد گنگ است، یعنی نمیتوان
آن را دقیقاً بصورت کسر
برابر باشد، زیرا π یک عدد گنگ است، یعنی نمیتوان
آن را دقیقاً بصورت کسر ![]() نوشت که در آن p و q اعداد صحیح هستند. این
واقعیت، که مدتها بود ریاضیدانان آن را حدس میزدند، برای اولین بار در سال 1768
توسط یوهان لمبرت (Johann Lambert) اثبات شد. از آن موقع
تا کنون اثباتهای مختلفی برای این قضیه ارائه شده. واضحترین نتیجه این قضیه این
است که π یک عدد بیانتها است
و بدون اینکه ارقام آن دوباره تکرار شوند، تا ابد ادامه پیدا میکند. این یعنی π یک عدد عشاری متناوب نیست. البته
این به این معنی نیست که یک دستهِ خاص از ارقام (مثل 1234) نمیتواند بارها در
آن تکرار شود؛ در واقع به احتمال زیاد چنین دستههایی به تعداد بینهایت در این
عدد تکرار میشوند. ولی شما نمیتوانید π را بصورت یک دسته متناهی از اعداد نشان دهید که تا ابد
تکرار میشود.
نوشت که در آن p و q اعداد صحیح هستند. این
واقعیت، که مدتها بود ریاضیدانان آن را حدس میزدند، برای اولین بار در سال 1768
توسط یوهان لمبرت (Johann Lambert) اثبات شد. از آن موقع
تا کنون اثباتهای مختلفی برای این قضیه ارائه شده. واضحترین نتیجه این قضیه این
است که π یک عدد بیانتها است
و بدون اینکه ارقام آن دوباره تکرار شوند، تا ابد ادامه پیدا میکند. این یعنی π یک عدد عشاری متناوب نیست. البته
این به این معنی نیست که یک دستهِ خاص از ارقام (مثل 1234) نمیتواند بارها در
آن تکرار شود؛ در واقع به احتمال زیاد چنین دستههایی به تعداد بینهایت در این
عدد تکرار میشوند. ولی شما نمیتوانید π را بصورت یک دسته متناهی از اعداد نشان دهید که تا ابد
تکرار میشود.
در
ریاضیات مقدماتی، برای اینکه از این مشکلات دوری کنند، مقدار π
را بصورت یک کسر ساده، مثل ![]() که با
که با ![]() برابر است، تقریب میزنند. شما برای اینکه ببینید
این کسر دقیقاً مساوی π
نیست، میتوانید به بسط
برابر است، تقریب میزنند. شما برای اینکه ببینید
این کسر دقیقاً مساوی π
نیست، میتوانید به بسط ![]() توجه کنید:
توجه کنید:
![]()
π=
3. 141592 …
ارقام ![]() نیز مانند هر عدد گویای دیگری دارای ارقامِ متناوبِ
تکرار شونده است، و در واقع ارقام اعشاری آن بصورت زیر است:
نیز مانند هر عدد گویای دیگری دارای ارقامِ متناوبِ
تکرار شونده است، و در واقع ارقام اعشاری آن بصورت زیر است:
![]() 3.142857142857142857…
3.142857142857142857…
و چیزی که
در آن تا ابد تکرار میشود دسته ارقام 142857 است.
در طول
تاریخ برای تخمین π
از کسرهای مختلفی استفاده شده.
در حدود
سالهای 1900 قبل از میلاد، ریاضیدانان بابلی برای تخمین π از کسر ![]() استفاده میکردند.
استفاده میکردند.
نسخه
خطی ریاضی رایند (Rhind
mathematical papyrus) در طول دوران دوم میانی
(درحدود 1650-1550 قبل از میلاد) توسط کاتبی بنام آمس نوشته شد. هرچند خود آمس میگوید
که او این را از روی نسخهخطی قدیمیتر دیگری کپی کرده که قدمت آن به 2055-1650
قبل از میلاد باز میگردد. این نسخه خطی شامل یک محاسبه تقریبی برای حساب کردن
مساحت یک دایره است، که اگر بخواهیم آن را به زبان امروزی بیان کنیم، در آن مقدار π توسط کسر ![]() برآورد شده. بااینحال معلوم نیست که آیا مصریان
باستان عدد ثابت بخصوصی را برای π
به رسمیت میشناختند یا نه.
برآورد شده. بااینحال معلوم نیست که آیا مصریان
باستان عدد ثابت بخصوصی را برای π
به رسمیت میشناختند یا نه.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
آنطور که
از ظاهر ![]() پیداست، شما انتظار ندارید که این کسر عدد خاصی
باشد. من هم همین عقیده را داشتم. ولی این به پیش از زمانی باز میگردد که نتیجه
برخی از تحقیقاتی که انجام دادم به این کسر منتهی شوند. ولی معلوم شده که این کسر
بطور نزدیکی با معماء مشهوری، بنام برج هانوی (Tower of
Hanoi)، و همچنین با شکل معروفتری بنام مثلث سرپینسکی (Sierpiński
gasket)، ربط دارد.
پیداست، شما انتظار ندارید که این کسر عدد خاصی
باشد. من هم همین عقیده را داشتم. ولی این به پیش از زمانی باز میگردد که نتیجه
برخی از تحقیقاتی که انجام دادم به این کسر منتهی شوند. ولی معلوم شده که این کسر
بطور نزدیکی با معماء مشهوری، بنام برج هانوی (Tower of
Hanoi)، و همچنین با شکل معروفتری بنام مثلث سرپینسکی (Sierpiński
gasket)، ربط دارد.
برج هانوی
یک معمای سنتی است که در سال 1883 توسط لوکاس (Lucas)
معروف شد. این معما شامل یک سری از دیسکهای دایرهای شکل با اندازههای متفاوت
است، که باید بر روی سه میله چیده شوند. در اینجا ما فرض میکنیم که تعداد دیسکهای
مورد نظر یک عدد صحیح مثبت باشد،
1, 2, 3, …, n. چنین معمایی را هانوی n-دیسکی مینامیم. معمولاً در پازلهایی که فروخته میشود
مقدار n 5 یا 6 است.
در ابتدا
همه دیسکها بر روی یک میله قرار دارند، و طوری چیده شدهاند که اندازه آنها از
پایین به بالا کوچکتر میشود. هدف از این معما این است که کلیه دیسکها به میلههای
دیگر انتقال داده شوند. با هر حرکت، یک دیسک از بالای یک میله به میله جدید انتقال
پیدا میکند. ولی دیسکها فقط میتوانند به طرق زیر جابجا شوند:
· تنها دیسکهایی میتوانند حرکت کنند که زیر
آنها دیسک بزرگتری قرار داشته باشد
· یا اینکه دیسکها به یک میله خالی انتقال
داده شوند
اولین
قاعد حاکی از این است که وقتی تمام دیسکها جابجا شدند، اندازه آنها باز هم از
پایین به بالا کاهش یابد.
پیش از
اینکه مطالب بعدی را مطالعه کنید، باید سعی کنید تا این معما را حل کنید. در ابتدا
کار خودتان را با دو دیسک شروع کنید و بعداً بسته به اینکه چقدر این معما برایتان
جالب است، تعداد دیسکها را به پنج یا شش دیسک افزایش دهید.
برای مثال، شما میتوانید یک هانوی 2-دیسکی
را تنها با سه حرکت حل کنید:
شکل 78. حل یک هانوی 2-دیسکی. دیسک 1 را به میله وسطی
انتقال دهید، سپس دیسک 2
را به راست، و سپس دیسک 1
را به راست منتقل کنید.
درباره یک هانوی 3-دیسکی چطور؟ شروع آن
به شکل زیر خواهد بود:

شکل 79. وضعیت شروع یک هانوی 3-دیسکی.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
کسور برای
اموری که با تقسیم سروکار داشته باشند بسیار مناسبند، و برای مدتها یونانیان
باستان عقیده داشتند که با کسور میتوان همه امور جهان را توصیف کرد.
اما پس از
آن یکی پیدا شد و در پیامد قضیه فیثاغورث این مسئله را مطرح کرد که نسبت اضلاع یک
مثلث قائمالزاویه به وتر آن چیست؟
پاسخ این
سؤال به آنها فهماند که برخی از مسائل هستند که نمیشود آنها را با کسور حل کرد.
اینجا بود
که اعداد گنگ (غیرگویا) متولد شدند.
اعداد
گویا به همراه اعداد گنگ، دستگاه اعداد حقیقی را تشکیل میدهند.
اعداد
گویا (یا همان کسرها) برای بسیاری از امور به اندازه کافی مناسب هستند، ولی برخی
از مسائل دارای جواب گویا نیستند. برای مثال، هندسهدانان یونانی دریافتند که قطر
مربعی که طول اضلاع آن 1 باشد، یک عدد گویا
نیست. اگر طول قطر چنین مربعی را x فرض کنیم، آنگاه قضیه فیثاغورث به ما میگوید که:
x2 =12+12 =2
بنابراین ![]() است. و آنها با اکراه فراوان ثابت کردند که این عدد
گویا نیست.
است. و آنها با اکراه فراوان ثابت کردند که این عدد
گویا نیست.
این مسئله هندسهدانان یونانی را واداشت که تمرکز
خود را بر روی طولهای هندسی بگذارند و اعداد را نادیده بگیرند. روش جایگزین این
بود که دستگاه اعداد گستردهتر شود تا بتواند این کمبود را جبران کند، و معلوم شد
که این فکر بهتری است.
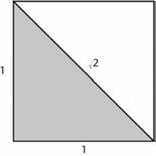
شکل 90. قطر یک مربع با طول واحد.
امروزه ما
اعداد را بصورت اعشاری مینویسیم. به دلایل عملی، ماشینهای حساب بعد از ممیز،
از تعداد ارقام اعشاری محدودی استفاده میکنند. در ابتدای این فصل ما دیدیم که طول
قطر یک مربع واحد، با ده رقم اعشار بصورت زیر است:
![]()
ولی
محاسبه نشان میدهد که اگر عدد فوق را به توان 2 برسانیم، مقدار دقیق
آن از این قرار است:
(1.4142135623)2=
1.999999999978325589129
گرچه این
عدد به 2 نزدیک است، ولی با آن مساوی نیست.
شاید ما
محاسبه را زود متوقف کردهایم. شاید اگر تا یک میلیون رقم اعشار محاسبه خود را
ادامه دهیم، جواب دقیقی را برای جذر 2 بگیریم. ولی در واقع
راه سادهای وجود دارد که نشان میدهد از این طریق نیز جواب دقیق به دست نمیآید.
اگر جذر را با ده رقم اعشار تخمین بزنیم، آخر آن به 3 ختم میشود. هنگامی
که ما مجذور این عدد را حساب میکنیم، یک عدد 20-رقمی را بدست میآوریم،
که به 9 ختم میشود، که 32
است. این تصادفی نیست؛ این پیآمد روشی است که ما اعداد اعشاری را درهم ضرب میکنیم.
آخرین رقم بامعنی هر عدد اعشاری، غیر از 0، یک رقم غیر صفر است.
بنابراین مجذور آن هم یک رقم غیر صفر منتهی میشود. بدلیل اینکه بسط اعشاری 2
با 2.0000… برابر است، که در آن فقط صفر
تکرار میشود، هیچ مجذوری نیست که بتواند دقیقاً با این عدد برابر باشد.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
ما به
اعداد شمردنی خیلی زود خو میگیریم، ولی اعدادی هستند که بسیار عجیبترند. اولین
عدد عجیبی که ما در ریاضیات با آن آشنا میشویم، عدد π است. سر و کله این عدد در بسیاری از حوزههای
ریاضیات پیدا میشود، حوزههایی که برخی از آنها ارتباطی با دایره ندارد.
ریاضیدانان تعداد ارقام π را تا
بیش از 12 تریلیون رقم محاسبه کردهاند. آنها چگونه
اینکار را انجام میدهند؟ درک اینکه π چگونه عددی است، باعث شد تا بسیاری از
مسائل باستانی ریاضی حل شود، که یکی از آنها مسئله تربیع دایره بود.
ما نخستین بار هنگامی با π مواجه میشویم که بخواهیم محیط و مساحت یک
دایره را حساب کنیم. اگر شعاع دایره r باشد، آنگاه محیط آن 2πr و مساحت آن r2π میشود.
از نظر هندسی این دو کمیت ارتباط مستقیمی با یکدیگر ندارند، بنابرای قابل توجه است
که عدد π در هر
دو آنها ظاهر میشود. یک روش ادراکی وجود دارد که با استفاده از آن میتوان به علت
این مسئله پی برد. دایره را به قطعات کوچکتری، مانند قاچهای پیتزا، تقسیم کنید، و
آنها را طوری کنار هم بچینید که تقریباً به شکل یک مستطیل درآیند. طول این مستطیل
تقریباً برابر با نصف محیط دایره است، که با rπ برابر
است. عرض یا ارتفاع آن هم تقریباً با r برابر است. بنابراین مساحت این مستطیل با
r2π r×r=π برابر
خواهد بود.
شکل 96. تقریب مساحت یک دایره.
ولی روش فوق
فقط تقریبی برای مساحت دایره است. شاید اعدادی که در رابطه با محیط و مساحت دایره
ظاهر میشوند بسیار شبیه هماند، ولی یکی نیستند. ولی چنین چیزی بعید است، زیرا
اگر ما برشها را هم نازکتر ببریم، باز هم این استدلال بر جای خود باقی است. اگر ما از تعداد زیادی از برشهای بسیار
نازک استفاده کنیم، این تقریب بسیار دقیق میشود. در واقع با افزایش خیلی زیاد برشها،
تفاوت میان دایره و یک مستطیل واقعی نیز بسیار کوچک میشود. استفاده از حدود
ریاضی اثبات میکند که فرمول مساحت دایره صحیح و دقیق است. و به همین دلیل است که عدد
π هم در
محیط و هم در مساحت یک دایره ظاهر میشود.
با
استفاده از حد نیز میتوانیم مساحت را تعریف کنم. مساحتها آنطور که ما فکر میکنیم ساده
نیستند. مساحت چند ضلعیهای را میتوان با تقسیم آنها به مثلثهای کوچکتر بدست
آورد، ولی اشکال انحناء دار را نمیتوان به این آسانی تقسیم کرد. حتی مساحت
مستطیلی که اضلاع آن نامتناسب باشند را نیز نمیتوان بسادگی تفسیر کرد. مسئله این
نیست که بگوییم مساحت چیست، و اندازه دو ضلع را در هم ضرب کنیم، بلکه مشکل
این است که ثابت کنیم فرمولی که ارائه میدهیم دقیقاً همان است که یک مساحت باید
باشد (مثلاً وقتی اشکال را به یکدیگر متصل میکنید تا مساحتهای آنها با هم جمع
شوند). ریاضیاتی که در مدارس تدریس میشود، به امید اینکه کسی متوجه این مسائل
نشود، یواشکی از روی آنها رد میشود.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
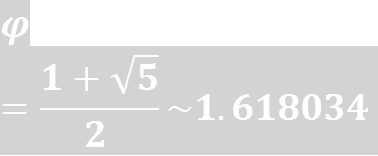
این عدد
بخاطر رابطهای که در هندسه اقلیدسی با پنجضلعی منظم و دوازده وجهی داشت، برای
یونانیان باستان شناخته شده بود. این عدد همچنین وابستگی نزدیکی با دنباله اعداد
فیبوناچی دارد [به فصل 8
رجوع کنید]، و برخی
از الگوهایی که در ساختار گیاهان و گلها وجود دارند را نیز توضیح میدهد. معمولا
به این عدد، عدد طلایی (golden number) گفته میشود،
نامی که بنظر میرسد بین سالهای 1826 تا 1835 به آن داده شده. حرفهای زیادی
درمورد خواص مرموز و زیباشناسانه این عدد گفته شده، ولی بیشتر این حرفها مبالغهآمیزاند،
و برخی از این ادعاها هم بر پایه آمارهای دروغین بنا شده، و برخی نیز کلاً بیپایهاند.
ولی با اینحال عدد طلایی خصوصیات ریاضی قابلتوجهی دارد، که از جمله آنها میتوان
به پیوندهایی که با اعداد فیبوناچی، و وابستگیهایی که با جهان طبیعی دارد، اشاره
کرد.
عدد φ[8] نخستین بار در رابطه
با پنجضلعیهای منظم در کتاب اصول اقلیدس ظاهر شد. مطابق با سنت آن دوره،
بجای اینکه آن را یک عدد در نظر بگیرند، از آن یک تفسیر هندسی داشتند.
برای بدست
آوردن φ
یک فرمول دقیق وجود دارد که من بزودی به آن اشاره میکنم. ولی مقدار اعشاری آن تا
شش رقم اعشار بصورت زیر است:
φ
= 1.618034
و تا 100
رقم اعشار:
φ = 1.6180339887498948482045868343656381177203091798057628
621354486227052604628189024497072072041893911375
یک خصوصیت
ویژه φ هنگامی آشکار میشود که ما معکوس آن (یعنی ![]() )
را حساب کنیم. مقدار این عدد تا شش رقم اعشار برابر است با:
)
را حساب کنیم. مقدار این عدد تا شش رقم اعشار برابر است با:
φ = 0.618034
این مبین
این است که φ =1+![]() .
این رابطه را میتوان بصورت معادله درجه دوم φ2= φ+1، یا به شکل معادله
استاندارد زیر نیز نوشت:
.
این رابطه را میتوان بصورت معادله درجه دوم φ2= φ+1، یا به شکل معادله
استاندارد زیر نیز نوشت:
φ2- φ -1 = 0
این
معادله دارای دو جواب زیر است:
![]() و
و ![]()
اگر مقدار
آنها را حساب کنیم، این دو عدد 1·618034 و -0·618034
هستند. ما برای تعریف φ،
مقدار مثبت را میگیریم. بنابراین
φ = 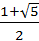
عدد طلایی
در هندسهِ پنجضلعیهای منظم ظاهر میشود. با پنجضلعی منظمی که طول اضلاع آن 1
است شروع میکنیم. پنج قطر را رسم کنید تا یک ستاره پنج پر بسازید. اقلیدس ثابت کرد
که طول هر یک از قطرها با عدد طلایی برابر است.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
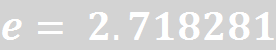
بعد از π، عدد
عجیب دیگری که ما (معمولاً در حسابان) با آن روبرو میشویم عدد e است. نام این عدد از حرف اول
کلمه ’ نمایی‘ (exponential)
در زبان لاتین گرفته شده. عدد e ابتدا در سال 1683 توسط ژاکوب برنولی (Jacob
Bernoulli) کشف شد. این عدد در مسائلی مثل بهره مرکب، لگاریتمها،
و متغیرهایی مثل دما، رادیواکتیویته، یا میزان افزایش یا کاهش جمیت انسانی ظاهر
میشود. اویلر e
را به π و i
پیوند داد.
هنگامی که
ما پول خود را بعنوان سپرده در بانک میگذاریم، یا وام میگیریم، باید برای سپرده خودمان
بهره دریافت کنیم، یا بابت وامی که گرفتهایم باید بهره بدهیم. برای مثال اگر ما
در بانکی 100 دلار سرمایهگذاری کردهایم که بهرهای معادل %10
در سال پرداخت میکند، ما پس از گذشت یک سال 110 دلار خواهیم گرفت.
برخی از
بهرهها مرکب (compounded) هستند. این یعنی
همانطور که به سپرده اصلی بهره اضافه میشود، به مجموع آنها نیز بهره تعلق میگیرد.
اگر نرخ بهره مرکب %10
در سال باشد، سود سرمایهگذاری 110
دلاری در طول سال بعد 11 دلار میشود،
درحالیکه سود سرمایهگذاری عادی تنها 10 دلار است. بنابراین
پس از گذشت دو سال از بهره مرکب 10درصدی، ما 121 دلار خواهیم داشت. در
سالِ سومِ بهره مرکب، 12.10 به این
سرمایه اضافه میشود و ما در مجموع 133.10 دلار خواهیم داشت، و
در سال چهارم این مجموع به 141.41 دلار میرسد.
ثابت
ریاضی e هنگامی مطرح میشود
که مثلاً بهره %100 داشته باشیم، تا پس از سپری شدن مدت زمان معین (مثلاً
یک قرن) سرمایه ما دو برابر شود. ما برای هر دلاری که سرمایهگذاری میکنیم، پس از
گذشت یک صد سال، دو برابر آن را خواهیم گرفت.
فرض کنید
بجای نرخ %100 در طول صد سال، ما نرخ %50 را در طول پنجاه سال
بکار ببریم، و آن را مرکب کنیم. پس از گذشت پنجاه سال ما خواهیم داشت:
1+0.5=1.5
پس از
گذشت 50 سال دوم (صد سال)، ما خواهیم داشت:
1.5 + 0.75=2.25
بنابراین
نسبت به بهره %100 قبلی، ما با گذشت صد سال سرمایه بیشتری را خواهیم داشت.
اگر ما یک
قرن را به سه قسمت مساوی تقسیم کنیم، و نرخ سود را نیز بر 3 تقسیم کنیم، یک دلار
ما بصورت زیر رشد میکند:
سرمایه اولیه 1
بعد از
گذشت ![]() دوره: 1.3333333333
دوره: 1.3333333333
بعد از
گذشت ![]() دوره: 1.7777777777
دوره: 1.7777777777
بعد از
گذشت 1 دوره: 2.3703703704
روی هم
رفته، این روش سود بیشتری را میدهد.
الگویی در
این اعداد هست که در زیر دیده میشود:
1=![]()
1.3333333333=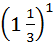
1.7777777777=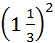
2.3703703704=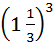
ریاضیدانان
میخواستند بدانند اگر نرخ بهره را بصورت پیوسته بکار ببرند چه میشود (یعنی در
طول دورههای کوچکتر و باز هم کوچکتر). این الگو به این صورت بیان میشود: اگر ما
دوره را به n
قسمت مساوی تقسیم کنیم، و نرخ بهره ![]() باشد، در پایان دوره ما این مقدار سرمایه را خواهیم
داشت:
باشد، در پایان دوره ما این مقدار سرمایه را خواهیم
داشت:
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
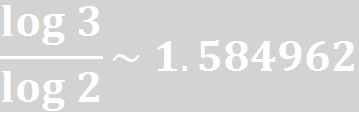
مانند ![]() ،
عدد عجیبِ بالا نیز یکی از خاصیتهای اصلی مثلثهای سِرپینسکی را تشکیل میدهد. ولی
عدد فوق مشخص کننده این است که منحنی معروف سرپینسکی چقدر ناهموار یا پرانحنا است.
مسائلی از این قبیل در هندسه فرکتال (fractal
geometry) مطرح میشوند. اینها روشهای جدیدی هستند که میتوان از
آنها برای مدلسازی اشکال پیچیده استفاده کرد. فراکتالها مفهوم بُعد را تعمیم
میدهند. یکی از مشهورترین فراکتالها، که مجموعه مندلبرو (Mandelbrot
set) نام دارد، شکل بینهایت پیچیدهای است که توسط یک
فرآیند بسیار ساده تعریف میشود.
،
عدد عجیبِ بالا نیز یکی از خاصیتهای اصلی مثلثهای سِرپینسکی را تشکیل میدهد. ولی
عدد فوق مشخص کننده این است که منحنی معروف سرپینسکی چقدر ناهموار یا پرانحنا است.
مسائلی از این قبیل در هندسه فرکتال (fractal
geometry) مطرح میشوند. اینها روشهای جدیدی هستند که میتوان از
آنها برای مدلسازی اشکال پیچیده استفاده کرد. فراکتالها مفهوم بُعد را تعمیم
میدهند. یکی از مشهورترین فراکتالها، که مجموعه مندلبرو (Mandelbrot
set) نام دارد، شکل بینهایت پیچیدهای است که توسط یک
فرآیند بسیار ساده تعریف میشود.
مثلثهای سرپینسکی [به فصل ![]() رجوع کنید] نمونه کوچکی از منحنیهایی هستند که در
اوایل قرن بیستم اختراع شدند، و در آغاز نام ’منحنیهای دیوانهوار‘ (pathological
curves) بر روی آنها گذاشته شد، که یک بار منفی به آنها میداد.
این بااصطلاح منحنیها، شامل منحنی برفدانهای (snowflake
curve) هلگه فون کوخ، و منحنیهای فضاپرکن (space-filling
curves) پینو (Peano)
و هیلبرت (Hilbert) هستند.
رجوع کنید] نمونه کوچکی از منحنیهایی هستند که در
اوایل قرن بیستم اختراع شدند، و در آغاز نام ’منحنیهای دیوانهوار‘ (pathological
curves) بر روی آنها گذاشته شد، که یک بار منفی به آنها میداد.
این بااصطلاح منحنیها، شامل منحنی برفدانهای (snowflake
curve) هلگه فون کوخ، و منحنیهای فضاپرکن (space-filling
curves) پینو (Peano)
و هیلبرت (Hilbert) هستند.
شکل 109. سمت چپ. منحنی برفدانهای. سمت راست. مراحل
مختلف ساخت منحنی فضا-پرکن هیلبرت.
در آن
زمان این منحنیها چندان جالب بنظر نمیرسیدند، آنها تنها مثالهای نقضی برای گذارههای
محتمل ریاضی بودند که درواقع غلط بودند. منحنی برفدانهای پیوسته (continuous)
است ولی در هیچ نقطهای مشتقپذیر (differentiable)
نیست؛ یعنی در هیچ نقطه قطع نمیشود ولی در همهجا دندانهدار است. این منحنی طولی
نامتناهی دارد ولی در سطحی متناهی محسور شده است. منحنیهای فضا-پرکن آنقدرها
متراکم نیستند، آنها حقیقتاً فضا را پر میکنند. هنگامی که ساخت آنها تقریباً
بینهایت بار ادامه یابد، منحنی حاصله از هر نقطه درون یک مربع توپُر (solid
square) عبور میکند.
برخی از
ریاضیدانان محافظهکار آن زمان این منحنیهایی را بیحاصل میدانستند و آنها را
مسخره میکردند. هیلبرت جزء معدود ریاضیدانان برجسته آن زمان بود که به اهمیت این
منحنیها پی برد و با اشتیاق فراوان از جدی گرفتن خواص آنها حمایت میکرد.
امروزه
دید ما نسبت به این منحنیها خیلی مثبتتر است. آنها پایههای حوزه جدیدی از
ریاضیات را تشکیل میدهند که به هندسه فراکتال معروف است و در دهه 1970
توسط مندلبرو پایهگذاری شد. این منحنیها صرفاً به دلایل ریاضی اختراع شده بودند،
ولی مندلبرو متوجه شد که از آنها میتوان برای روشن شدن بینظمیهای موجود در
جهانِ طبیعت نیز استفاده کرد. او به این اشاره کرد که مثلثها، مربعها، دایرهها،
مخروطها، و دیگر اشکالِ سنتی هندسه اقلیدسی ساختار زیبایی ندارند. اگر شما یک
دایره را بزرگ کنید، همانند یک خط مستقیم بیریخت است. ولی بسیاری از اشکال طبیعت،
در هر مقیاسی که به آنها نگاه شود، دارای ساختارهای پیچیدهای هستند. مندلبرو مینویسد
”ابرها به شکل کره نیستند، کوهها مخروطی شکل نیستند، سواحل به شکل دایره نیستند،
و برگ درختان صاف نیست، حتی رعد و برق نیز به خط مستقیم حرکت نمیکند.“ البته
اینها حقایقی هستند که هر کسی آنها را میداند، ولی این مندلبرو بود که به اهمیت
آنها پی برد.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
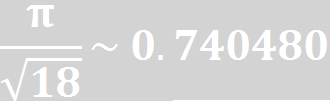
عدد ![]() یکی از اعداد مهم در ریاضیات، فیزیک، و شیمی است.
هنگامی که ما گویهای یکسان را طوری در کنار هم فشرده میکنیم که فضای میان آنها
به حداقل ممکن برسد، این عدد بخشی از آن فضا است که پر میشود. کپلر در سال 1611
این عدد را حدس زد، ولی این حدس اثبات نشده باقی ماند تا اینکه توماس هِلز (Thomas
Hales) در سال 1998 با کمک کامپیوتر اثباتی برای آن پیدا کرد.
یکی از اعداد مهم در ریاضیات، فیزیک، و شیمی است.
هنگامی که ما گویهای یکسان را طوری در کنار هم فشرده میکنیم که فضای میان آنها
به حداقل ممکن برسد، این عدد بخشی از آن فضا است که پر میشود. کپلر در سال 1611
این عدد را حدس زد، ولی این حدس اثبات نشده باقی ماند تا اینکه توماس هِلز (Thomas
Hales) در سال 1998 با کمک کامپیوتر اثباتی برای آن پیدا کرد.
ما کار
خود را با یک سؤال سادهتر آغاز میکنیم، یعنی چگونگی متراکم کردن دایرهها در
صفحه. اگر بخواهید تا آنجا که امکان دارد، تعدادی سکه یکسان را در پهلوی یکدیگر
قرار دهید، متوجه خواهید شد که یک چیدمان بدون نظم فضای زیادی را تلف خواهد کرد.
اگر سعی کنید با تنگ کردن فاصله میان آنها فضای اضافه را از بین ببرید، آنگاه بنظر
میرسد اگر آنها بشکل شانهعسلی (ششگوشه) درکنار یکدیگر قرار گیرند فضای خالی
بطور موثرتری متراکم خواهد شد.
ولی حداقل
دور از ذهن نیست که شاید بتوان با چیدمان هوشمندانهتری آنها را بطور متراکمتری
درکنار هم قرار داد. اگر چیدمانهای مختلف را آزمایش کنیم، خواهیم دید که چنین
چیزی غیر محتمل بنظر میرسد، ولی ثابت نمیکند که الگوی شانهعسلی بهترین چیدمان
است. سکههای یکاندازه را میتوان بصورت بیشماری درکنار یکدیگر قرار داد،
بنابراین هیچ آزمایشی نیست که بتواند همه آنها را بررسی کند.
برخلاف چیدمان تصادفی، الگوی ششگوش بسیار منظم و
متقارن است. این الگو همچنین مستحکم (rigid)
نیز هست، یعنی شما نمیتوانید هیچ یک از سکهها را حرکت دهید، زیرا سکههای دیگر
جای آنها را پر خواهند کرد. در نگاه اول بنظر میرسد یک چیدمان مستحکم، به بهترین
شکل فضا را پر میکند، زیرا نمیتوان با حرکت سکهها این چیدمان را به چیدمان
بهتری تغییر داد.

شکل 117. سمت چپ: با یک چیدمان تصادفی، فضای زیادی
هدر داده خواهد شد. سمت راست: یک الگوی شانهعسلیِ ششگوش به بهترین نحو فضاهای
خالی را پر میکند.
البته
چیدمانهای مستحکم دیگری نیز وجود دارند که تاثیر آنها کمتر است. بیایید چیدمان
منظم دایرهها را با دو چیدمان که واضح بنظر میرسند شروع کنیم:
· شبکههای شانهعسلیِ ششگوش. این الگو به
این دلیل شش گوش نامیده میشود چون با اتصال مراکز دایرهها به یکدیگر، ششضلعی
تشکیل میشود.
· شبکههای مربع شکل. در اینجا دایرهها مانند
مربعهای شطرنج در کنار یکدیگر قرار میگیرند.

شکل 118. سمت چپ: شش مرکز متصل به یکدیگر یک ششضلعی
منظم را تشکیل دادهاند. سمت راست. چیدمان دایرهها بصورت مربعی درکنار هم.
الگوی
مربعی نیز مستحکم است، ولی دایرهها بصورتی درکنار هم متراکم شدهاند که کارآیی
کمتری دارد. اگر شما یک الگوی خیلی بزرگ را تشکیل دهید، شبکه ششضلعی فضای بیشتری
را میپوشاند (و فضا خالی کمتری باقی میماند).
ریاضیدانان
برای اینکه این مسئله را دقیقتر بیان کنند، فرض میکنند که ناحیه مورد نظر بسیار
بزرگ شود، آنگاه مفهوم چگالی (density)
متراکمسازی دایرهها را بصورت حدِ نسبتِ مساحتِ مربوطه، به مساحت کُل دایرهها
تعریف میکنند. بطور غیرمستقیم، هدف این است که کل صفحه با دایرهها پر شود
و نسبت مساحت ناحیه پوشیده شده حساب شود. اگر بخواهیم این نسبت را بصورت تحتالفظی
بیان کنیم میشود ![]() ،
که بیمعنی است، بنابراین ما ناحیه بزرگی را با تعداد زیادی مربع میپوشانیم و حد
آن را در بینهایت حساب میکنیم.
،
که بیمعنی است، بنابراین ما ناحیه بزرگی را با تعداد زیادی مربع میپوشانیم و حد
آن را در بینهایت حساب میکنیم.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
ثابت اپِری (Apéry’s
Constant) نمونه برجستهای از یک الگوی ریاضی است که برای همه
اعداد زوج کار میکند، ولی تا آنجایی که ما میدانیم، بنظر میرسد که برای اعداد
فرد اینطور نیست. اثبات اینکه این عدد گنگ است کاملاً غیره منتظره بود.
آیا تابع زتای
ریمان را بخاطر دارید؟ [به فصل ![]() رجوع کنید] این تابع براساس برخی از اصطلاحات فنی
درباره پیوستگی تحلیلی توسط سری زیر تعریف میشود:
رجوع کنید] این تابع براساس برخی از اصطلاحات فنی
درباره پیوستگی تحلیلی توسط سری زیر تعریف میشود:
z(z)= ![]()
که در آن z یک عدد مختلط است.
هنگامی که اویلر مسئله بازل را حل کرد، ریاضیدانان قرن هجدهم نیز ابتدا در حالت z=2 با این سری بینهایت روبرو شدند. به عبارتی، این
مسئله نیاز داشت تا فرمولی برای z(2)
پیدا شود، یعنی مجموع معکوس مربعهای اعداد صحیح. ما در فصل [π] دیدیم که اویلر در سال 1735جواب این مسئله را پیدا
کرد:
z(2)= ![]()
از همان
روش میتوان برای توانهای چهارم، ششم، و هر توان زوج مثبت دیگری استفاده کرد:
z(4)= ![]()
z(6)= ![]()
و این
الگو برای 8 ، 10 و ... غیره نیز ادامه
دارد:
z(8)=![]() z(2) =
z(2) = ![]()
z(12) =![]() z(14) =
z(14) = ![]()
بر اساس
این مثالها، ممکن است ما انتظار داشته باشیم که مجموع مکعبهای وارونه نیز حاصل
ضرب یک عدد گویادر 3π باشد، یا مجموع توانهای
پنجم نیز حاصل ضرب یک عدد گویادر 5π باشد،
و به همین ترتیب. ولی محاسبات عددی قویاً حاکی از این هستند که این فرض اشتباه
است. در واقع تا کنون هیچ فرمولی برای این سریها کشف نشده که با π ارتباط داشته باشد یا نداشته
باشد. سِریهای فرد تابع زتا بسیار اسرارآمیز هستند.
بدلیل
اینکه π عدد غیرگویایی است،
که متعالی نیز هست، همه سریهای فوق دارای مجموعهای غیرگویا هستند. بنابراین اگر n= 2, 4 , 6, … باشد، آنگاه
z(n) غیرگویا است. ولی ما نمیدانیم که آیا این مسئله
برای توانهای فرد نیز صدق میکند یا نه. چنین چیزی خیلی محتمل بنظر میرسد، ولی
درک z(n) برای توانهای فرد
بسیار سختتر است، زیرا روشهایی که اویلر از آنها استفاده میکرد به زوج بودن n
تکیه داشتند. بسیاری از ریاضیدانان
با این مسئله کلنجار رفتند، و در کل به جایی نرسیدند.
هنگامی که
n=3 باشد، اگر مجموع معکوس مکعبها
را محاسبه کنیم، به عددی میرسیم که ثابت اَپِری نام دارد:
z(3)= ![]()
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
این عدد
در بسیاری از حوزههای آنالیز ریاضی و نظریه اعداد ظاهر میشود. معلوم است که این یک
عدد حقیقی است، به احتمال بسیار زیاد غیرگویا نیز هست، و به همین دلیل هم هست که
من آن را در اینجا آوردهام. این عدد از سادهترین تقریب برای مجموع معکوس کلیه
اعداد صحیح تا مقدار خاصی ظاهر میشود. برخلاف سادگی و حضور همه جانبه این عدد، ما
اطلاعات خیلی کمی درباره آن داریم. بویژه اینکه هنوز کسی نتوانسته ثابت کند
که این عدد گنگ است. ولی ما میدانیم که اگر گویا باشد، باید بسیار پیچیده باشد،
یعنی کسری که نشان دهنده این عدد است باید شامل اعداد بسیار بزرگی باشد که طول
مخرج آنها از 240,000 رقم بیشتر است.
اعداد هارمونیک (Harmonic
Numbers)، یک مجموع متناهی از معکوس اعداد صحیح هستند:
![]()
هیچ فرمول
آشکار جبری برای بدست آوردن Hn
بدست نیامده، و بنظر هم نمیرسد که چنین فرمولی وجود داشته باشد. ولی با استفاده
از حسابان خیلی ساده میتوان نشان داد که Hn بطور تقریبی با
لگاریتم طبیعی n برابر است. درواقع یک تقریب بهتر برای آن وجود دارد که بصورت زیر است:
Hn ~ log n
+ γ
که در
اینجا γ
یک ثابت است. همانطور که n بزرگتر میشود، اختلاف میان دو طرف نیز تا آنجا که ما بخواهیم کوچکتر میشود.
مقدار
عددی γ بصورت زیر است:
γ
= 0.5772156649015328606065120900824024310421...
در سال
2013 Alexander Yee
مقدار آن را تا 19,377,958,182 رقم اعشار
محاسبه کرد. بدلیل اینکه این عدد برای اولین بار در مقالهای آمده بود که اویلر آن
را در سال 1734 نوشت، حالا به ثابت اویلر (Euler’s
constant) شناخته میشود. او مقدار این عدد را تا 16
رقم اعشار حساب کرد. در سال 1790 لورنزو ماسچرونی (Lorenzo
Mascheroni) نیز مطالبی را در مورد این عدد منتشر کرد. او تلاش کرد
که مقدار این عدد را تا 32 رقم اعشار حساب کند،
ولی از رقم بیستم تا بیست و دوم را اشتباه حساب کرد. گاهی اوقات از این عدد به
نام ثابت اویلر-ماسچرونی نام میبرند، ولی در کل سزاوارتر است تا بیشترِ اعتبار را
به اویلر بدهیم. از دهه 1830 ریاضیدانان علامت این عدد را به γ تغییر دادند، و حالا
نیز از همین علامت استفاده میشود.
ثابت
اویلر در بسیاری از فرمولهای ریاضی ظاهر میشود، بویژه آنهایی که با سریهای
نامتناهی و انتگرالهای معین در حسابان رابطه دارند. در نظریه اعداد، عدد eγ معمول است. حدس زده
میشود که ثابت اویلر یک عدد متعالی باشد، ولی تا به امروز حتی اثبات نشده که این
عدد گنگ باشد. محاسبات انجام شده بر روی کسرهای مسلسلِ این عدد نشان میدهند که
اگر γ گویا باشد، و بتوان
آن را به شکل یک عدد کسری ![]() نوشت، آنگاه q باید حداقل 10242,080
باشد.
نوشت، آنگاه q باید حداقل 10242,080
باشد.
فرمول
دقیقتری نیز برای اعداد هارمونیک وجود دارد که بصورت زیر است:
![]() γ
+
γ
+ ![]()
که خطای
آن حداکثر ![]() است.
است.
حالا ما
دوباره توجه خود را به اعداد صحیح معطوف میکنیم، که به نوبه خودشان دارای جذابیت
خاصی هستند. هر کدام از آنها شخصیت مخصوص به خودش را دارد، همراه با ویژگیهای
خاصی که آن را جالب میکند.
در واقع
همه اعداد جالب هستند. اثبات: اگر اینطور نیست، باید کوچکترین عددی وجود
داشته باشد که جالب نباشد. ولی چنین چیزی باعث میشود که این عدد جالبی باشد، و
این خلاف فرض اولیه است.
ما
معمولاً فضا را طوری درنظر میگیریم که گویی سه بُعد دارد. در قلمرو نظریه نسبیت (relativity)،
برای چیزی که به فضا-زمان (space-time)
معروف است، زمان بُعد چهارم آن را فراهم میآورد. ولی تحقیقات جاری در فیزیک پیشرفته،
که به نظریه ریسمان (string theory)، و خصوصاً نظریه ام (M-theory)،
شناخته میشوند، این نظر را مطرح میکنند که درواقع فضا-زمان دارای یازده
بُعد است. از میان این یازده بعد، هفت عدد از آنها از دید یک انسانِ بیابزار
ناپیدا هستند. درواقع آنها هنوز هم بطور قطعی توسط یک آزمایش آشکارسازی نشدهاند.
چنین چیزی
ممکن است ناراحت کننده بنظر برسد، و حتی ممکن است درست هم نباشد. ولی فیزیک بارها
به ما نشان داده که آن تصویری که جهان از خودش به حواس ما ارائه میدهد میتواند
بطور قابل ملاحظهای با واقعیت متفاوت باشد. برای مثال، موادی که بظاهر بهم پیوستهاند،
از ذرات کوچکتری بنام اتم تشکیل شدهاند. حالا برخی از فیزیکدانان معتقدند که فضای
واقعی از آنچه ما فکر میکنیم خیلی متفاوتتر است. دلیل انتخاب 11
بُعد چیزی نیست که بر اساس مشاهدات واقعی پیشنهاد شده باشد، بلکه دلیل انتخاب آن
این است که باعث میشود یک ساختارِ بسیار مهمِ ریاضی بطور سازگاری عمل کند. نظریه
ریسمان خیلی فنی است، ولی میتوان اصول آن را بشکل طرحهای سادهای بیان کرد.
نسبیت و مکانیک کوانتوم (Quantum
mechanics) دو دستآورد بزرگ فیزیک نظری هستند. اولی توسط انیشتین (Einstein)
مطرح شد و نیروی گرانش را بصورت انحنای فضا-زمان توضیح میدهد. بر اساس نسبیت عام
(که اینشتین آن را پس از نسبیت خاص خودش، یعنی نظریه فضا، زمان، و ماده معرفی کرد)
ذرهای که از یک مکان به مکان دیگری میرود از یک مسیر ژئودوزیک (geodesic)
پیروی میکند. ژئودوزیک کوتاهترین مسیری است که دو مکان را به یکدیگر متصل میکند.
ولی در مجاورت یک جسم سنگین، مثل یک ستاره، فضا-زمان تغییر شکل میدهد، و این باعث
میشود تا مسیر خمیده بنظر برسد. برای مثال، سیارات در مسیری بیضیشکل به دور خورشید
میچرخند.
نظریه
اولیه گرانش، که توسط نیوتن (Newton)
کشف شد، این خمیدگی را بعنوان نتیجه اعمالِ یک نیرو تفسیر میکند، و برای اندازهگیری
قوت این نیرو یک فرمول ریاضی ارائه میدهد. ولی اندازهگیریهای بسیار دقیق نشان میدهند
که نظریه نیوتون کمی غیردقیق است. اینشتین نیروی گرانش را با انحنای فضا-زمان
جایگزین کرد، و این نظریه جدید توانست خطاهای نظریه نیوتون را تصحیح کند. از آن
موقع تاکنون نیز بارها صحت آن توسط رصدها مختلف، که عمدتاً شامل اجرام آسمانی
دوردست هستند، تایید شده.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
یک پنجمربعی (pentomino)
شکلی است که از قرار دادن پنج مربع یکسان درکنار یکدیگر ساخته میشود. اگر انعکاسها
را بحساب نیاوریم، برای اینکار 12 حالت ممکن وجود دارد.
بر طبق عرف، هر یک از این دوازده شکل مختلف را با یکی از حروف الفبا نشان میدهند
که شبیه آنها باشد. همچنین عدد 12، عدد مماسی در فضای
سه-بعدی نیز ه تقسیم بخشناپذیرست.

شکل 134. 12 پنجمربعیهای (pentominoes) مختلف.
بطور کلی یک n-مربعی شکلی است که از قرار
دادن n مربع یکسان درکنار هم ساخته میشود. رویهم رفته چنین اشکالی چندمربعی (polyominoes)
نامیده میشوند. اگر n=6 باشد ما 35 ششمربعی (hexominoes)،
و اگر n=7 باشد ما 108 هفتمربعی (heptominoes)
داریم.

شکل 135. 35 ششمربعی

شکل 136. 108 هفمربعی.
مفهوم کلی
چندمربعیها و اسامی آنها در سال 1953 توسط سولومون گولومب (Solomon
Golomb) اختراع شد، و توسط مارتین گاردنر در مجله Scientific American معروف شد.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
برخلاف انتظار
دیگران، گاوس در جوانی کشف کرد که به کمک خطکش و پرگار (غیر مدرج) میتوان یک 17-ضلعی
منظم را ترسیم کرد، کاری که نه فقط اقلیدس، بلکه هیچ کس دیگری برای بیش از 2000
سال تصور آن را نمیکردند.
برای
الگوهای کاغذدیواری 17 نوع تقارن مختلف وجود دارد. در
واقع چنین چیزی مانند یک نسخه دو-بعدی بلورشناسی است.
در مدل
استاندارد فیزیک ذرات، 17 گونه مختلف از ذرات
بنیادی وجود دارد [به فصل 11
رجوع کنید].
چندضلعی (polygon)
شکلی است که اضلاع آن از خطوط راست تشکیل شده باشد. اگر همه اضلاع با هم مساوی
باشند، و زاویهای که باهم تشکیل میدهند برابر باشد، آنگاه این شکل یک چندضلعی منظم (Regular
Polygon) است.
چندضلعیهای منظم نقش عمدهای در هندسه اقلیدسی بازی
میکنند، و از قدیم برای بسیاری از حوزههای ریاضی حیاتی بودهاند. یکی از اهداف
اصلی کتاب اصول اقلیدس این بود که ثابت کند دقیقاً 5 چندوجهی منظم (اجسام
سه بعدی که وجوه آنها با هم مساویند) وجود دارند.

شکل 141. چندضلعیهای منظم با 3، 4، 5، 6، 7، و 8 ضلع. اسامی آنها عبارت است
از مثلث متساویالاضلاع، مربع، و پنجضلعی، ششضلعی، هفضلعی، و هشتضلعی منظم.
چندضلعیهای
منظم به طریقی یکسانی در هر گوشه چیده میشوند [به فصل 5 رجوع کنید]. برای این منظور اقلیدس باید وجههایی را
درنظر میگرفت که چندضلعی منظم هستند و 3، 4،
و 5 ضلع دارند. در وجوه چندوجهیهای منظم، تعداد اضلاع
بیشتری ظاهر نمیشوند.
ضمناً
اقلیدس نیاز داشت تا با استفاده از ابزارهای سنتی، یعنی پرگار و خطکش غیر مدرج،
این اشکال را رسم کند، دلیل آن هم این بود که فنون هندسی وی بر پایه این فرض قرار
داشت که با این ابزارها میتوان اینکار را انجام داد. از طریق سادهترین ترسیمها
میتوان یک مثلث متساویالاضلاع و یک ششضلعی منظم را رسم کرد. خود پرگار میتواند
گوشهها را پیدا کند. برای رسم اضلاع به خطکش نیاز است، ولی تنها نقشی که در
اینکار دارد همین است.
رسم یک مربع
کمی سختتر است، ولی هنگامی که شما فهمیدید که چگونه یک زاویه قائمه را تشکیل
دهید، اینکار هم ساده میشود.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
در یک
بازی فوتبال معمولاً 23 نفر درگیر هستند: دو تیم 11 نفره بعلاوه یک داور (البته صرف نظر از کمکداورها). احتمال اینکه در میان این 23
نفر، روزِ تولد دو نفر از آنها در یک روز باشد چقدر است؟
جواب این
مسئله شگفانگیز است، مگر اینکه شما قبلاً پاسخ آن را بدانید.
برای
اینکه محاسبات را سادهتر کنیم، فرض را بر این میگذاریم که 365 روزِ تولد مختلف
داریم (از سالهای کبیسه صرف نظر میکنیم)، و هر یک از این روزها به یک اندازه
محتمل هستند، یعنی احتمال هریک از آنها ![]() است. ارقام واقعی اختلافی کوچک، ولی قابل ملاحظه را
نشان میدهند، زیرا برخی از روزها یا زمانهای سال از بقیه محتملتر هستند؛ این
اختلافها از کشوری به کشور دیگر متفاوت هستند. ولی حتی اگر شما این عوامل را نیز
بحساب آورید، در احتمال مورد نظر تغییر زیادی حاصل نمیشود، و چیزی که مهم است
نتیجه شگفت انگیز این مسئله است.
است. ارقام واقعی اختلافی کوچک، ولی قابل ملاحظه را
نشان میدهند، زیرا برخی از روزها یا زمانهای سال از بقیه محتملتر هستند؛ این
اختلافها از کشوری به کشور دیگر متفاوت هستند. ولی حتی اگر شما این عوامل را نیز
بحساب آورید، در احتمال مورد نظر تغییر زیادی حاصل نمیشود، و چیزی که مهم است
نتیجه شگفت انگیز این مسئله است.
ما همچنین
فرض میکنیم که احتمال هر بازیگر، مستقل از بازیگران دیگر است (که مثلاً اگر
بازیکنان طوری انتخاب شوند که روز تولد متفاوتی داشته باشند، این صحیح نخواهد
بود).
یک مسئله
مرتبط، ولی آسانتر، این است که احتمال اینکه روزِ تولدِ همه 23 بازیکن باهم متفاوت
باشند چقدر است. آنگاه قواعد محاسبه احتمالات به ما میگوید که باید این عدد را از
1 کم کنیم تا جواب سؤال اولیه خود را بدست آوریم. قاعدهای
که به آن اشاره کردم میگوید برای اینکه احتمال اتفاق نیفتادن یک رویداد را حساب
کنیم، باید احتمال اتفاق افتادن آن را از 1 کم کنیم. برای
روشنتر شدن محاسبات، مفید است فرض کنیم که بازیکنان یکی یکی به زمین وارد میشوند.
· هنگامی که نفر اول وارد میشود، فرد دیگری حضور
ندارد. بنابراین احتمال اینکه روز تولد او با فرد دیگری متفاوت باشد برابر 1
است (یعنی حتماً اینطور است).
· هنگامی که نفر دوم از راه برسد، روز تولد او
باید از نفر اول متفاوت باشد، بنابراین از میان 365 روز، 364
انتخاب دیگر وجود دارد. احتمال اینکه چنین چیزی اتفاق بیافتند برابر است با:
![]()
· هنگامی که نفر سوم وارد میشود، روز تولد
تولد وی باید با دو نفر اول متفاوت باشد، بنابراین از میان 365 روز 363 انتخاب دیگر وجود دارد. قواعدِ حسابِ احتمالات به ما میگوید که اگر
بخواهیم احتمال روی دادن دو اتفاقی را حساب کنیم که مستقل از یکدیگر هستند، باید
احتمال روی دادن هر یک از آنها را در هم ضرب کنیم. بنابراین تا اینجا
احتمال اینکه هیچ یک از این اشخاص دارای روزِ تولد یکسانی نباشند برابر است با
![]() ×
× ![]()
· هنگامی که نفر چهارم از راه میرسد، روز
تولد او نیز باید از باید از بقیه متفاوت باشد، بنابراین از میان 365
روز 362 انتخاب میماند. بنابراین تا اینجا احتمال
اینکه هیچ یک از این اشخاص دارای روز تولد یکسانی نباشند برابر است با
![]() ×
×
![]() ×
×
![]()
· حالا دیگر باید الگو برای شما روشن شده
باشد. پس از اینکه k
نفر وارد شدند، احتمال اینکه همه این k نفر روز تولد متفاوتی داشته باشند عبارت است از:
p(k)= ![]() ×
×
![]() ×
×
![]() ×
… ×
×
… × ![]()
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
وقتی صحبت
بر سر کُد[9]
باشد، خیلیها ممکن است بیاد جیمز باند و فیلم ’جاسوسی که از سرد سیر آمد‘ بیافتند.
ولی امروزه نیازی نیست تا کسی مثل جیمزباند باشی تا سر و کارت به کُدها بیافتد.
اگر راستش را بخواهید، امروزه همه ما بصورت کاملاً عادی و قانونی در زندگی روزمره
خودمان از کُدهای سِری استفاده میکنیم. عملیات بانکی اینترنتی یکی از همین کارها
است. ارتباط ما با بانک مورد نظر کدگذاری (encrypted)
میشوند (یعنی بصورت کدهای سری در میآیند) تا تبهکاران نتوانند پیامهای ما را
بخوانند و به پولهای ما دسترسی پیدا کنند (حداقل نه به آسانی).
در زبان
انگلیسی 26 حرف الفبا وجود دارد، و اغلب کدهای عملی از عدد 26 استفاده میکنند. بویژه در ماشین انیگما (Enigma)،
که در جنگ جهانی دوم توسط آلمانیها بکار گرفته میشد، از موتورهایی استفاده میشد
که 26 جایگاه مختلف برای حروف متناظر داشتند. ولی در این
زمینه هیچ ویژگی ریاضی خاصی بکار گرفته نشده بود، و اصول مشابهای برای اعداد دیگر
برقرار است.
تاریخ
رمزگذاری حداقل به حدود 1900 سال پیش از میلاد، و به مصر باستان باز میگردد.
بعدها جولیوس سِزار (Julius
Caesar) برای مکاتبات شخصی و نظامی خود از یک کُد ساده استفاده
کرد. در زندگینامه او آمده: ’اگر سِزار مطلب محرمانهای داشت که میخواست آن را
به دیگران بگوید، او آنها را با تغییر ترتیب حروف البفا بصورت رمزی مینوشت تا
نشود لغات را خواند. اگرکسی میخواست آنها را از رمز در آورد و معنی آنها را متوجه
شود، او باید حروف الفبا را با چهار حرف جلوتر جایگرین میکرد‘.
در زمان
سزار حروفی مانند J،
U و W وجود نداشت، ولی بدلیل اینکه
حرف فعلی ملموستر هستند، ما نیز از آنها استفاده میکنیم. روش کار وی به اینصورت
بود که الفبا را به ترتیب عادی خودشان بنویسد، و سپس در زیر حروف، نسخه تغییر
یافته آنها را بنویسد، چیزی شبیه زیر:
A
B C D E F G H I J K L MN O P Q R S T U V WX Y Z
F
G H I J K L MN O P Q R S T U V WX Y Z A B C D E
حالا شما
میتوانستید هر پیام را با استفاده از حروف متناظر آنها رمزگذاری یا رمزگشایی
کنید. این یعنی A
به F و B به G و ... تبدیل میشوند. مثل زیر:
J
U L I U S C A E S A R
O
Z Q N Z X H F J X F W
برای اینکه یک دستگاه عملی داشته باشیم تا بطور
خودکار حروف را بپیچاند، ما حروف را در یک دایره یا استوانه قرار میدهیم:

شکل 155. یک دستگاه عملی برای پیچاندن حروف.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
ثابت شده
که چیدمان گویهایی که تعداد آنها 56 گوی یا کمتر است، و
’پوسته محدب‘ آنها دارای کمترین حجم هستند، همیشه به شکل یک سوسیس است.
برای فهم این نتیجه، ابتدا بیایید چیز سادهتری را
بررسی کنیم، و آن بستهبندی دایرهها است. فرض کنید شما میخواهید تعداد زیادی از
دایرههای یکسان را در صفحه بستهبندی کنید، و آنها را با کوتاهترین انحنایی که
میتوانید، بطور محکم در یک پلاستیک لفافهبندی. این منحنی از نظر فنی یک پوسته محدبِ (convex
hull) متشکل از دایرهها نامیده میشود. مثلاً اگر هفت دایره
داشته باشیم، شما میتوانید یک ’سوسیس‘ دراز را امتحان کنید:

شکل 161. شکل سوسیسی و بسته بندی.
ولی فرض
کنید شما میخواهید کل مساحت درون منحنی را تا آنجا که ممکن است کوچک کنید.
اگر هر دایره دارای شعاع 1 باشد، آنگاه
مساحت شکل سوسیسی عبارت خواهد بود از:
24 + π=27.141
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
برای قرنها
تنها هندسهای که وجود داشت هندسه اقلیدسی بود. گمان میرفت که این هندسه بیانگر
فضای واقعی باشد، و این یعنی هیچ هندسه دیگری نمیتوانست وجود داشته باشد. ما
امروزه دیگر به هیچ یک از این گفتهها باور نداریم. انوع زیادی از هندسههای نااقلیدسی (non-Euclidean)
وجود دارند که با انحنای سطوح در فضا متناظرند. نسبیت عام نشان داد که فضا-زمان
واقعی، در مجاورتِ اجسامِ سنگینی مثل ستارگان، صاف نیست بلکه انحنا دارد [به فصل 11 رجوع کنید]. نوع دیگری از هندسه، که هندسه تصویری (projective
geometry) نام دارد، از پِرسپکتیو (perspective)
هنری ناشی شده بود. حتی هندسههایی نیز وجود دارند که تعداد نقاط آنها متناهی است.
سادهترین آنها دارای هفت نقطه، هفت خط، و 168 تقارن است. این مسئله
به داستان شگفتانگیز گروههای ساده متناهی (finite
simple groups) منجر شد، که در گروه عجیبی که به هیولا (monster)
شهرت دارد به اوج خود میرسند.
بدلیل
اینکه یک کره شباهت زیادی با شکل زمین دارد، از همان زمانی که بشر شروع به
دریانوردی به دور زمین کرد، هندسه کُروی (هندسه بر روی سطح یک کره) نیز اهمیت
زیادی پیدا کرد. ولی این شباهت خیلی دقیق نبود، شکل زمین بیشتر شبیه یک کُرهگون (spheroid)
است، که در قطبهای خود مسطح است. ولی خودِ دریانوردی هم علم دقیقی نبود. بهر حال
در فضای اقلیدسی، کره یک سطح بحساب
میآمد، بنابراین این حس وجود داشت که هندسه کروی نوع جدیدی از هندسه نیست، بلکه
فقط حالت خاصی از هندسه اقلیدسی است. هر چه باشد، حتی اگر یک مثلث بر روی سطح صافی
هم قرار نداشته باشد و مثلاً بر روی یک کره رسم شود، هیچ کس فکرش را هم نمیکرد که
هندسه این مثلث تفاوت عمدهای با هندسه اقلیدسی داشته باشد.
هنگامی که
ریاضیدانان شروع به بررسی دقیقتر یکی از ویژگیهای هندسه اقلیدسی کردند، کلیه این
تصورات عوض شد. این ویژگی، وجود خطوط موازی بود. خطوط موازی خطوطی هستند که از هر
طرف امتداد داده شوند، هیچ وقت یکدیگر را قطع نمیکنند. اقلیدس فهمیده بود که خطوط
موازی ظرافتهای خاصی دارند، به همین دلیل هم بود که او یکی از اصول موضوعه هندسه
خود را به وجود آنها اختصاص داده بود.
بسیاری از
اصول موضوعه (axioms) اقلیدس، مثل اینکه
’هر دو زاویه قائمه با هم برابرند‘، ساده و قابل درک بودند. درمقابل، اصل توازی
کمی مبهم بود. این اصل چنین میگوید: ’اگر دو خط راست بهوسیله یک خط سوم قطع
شوند، در همان طرفی از خط سوم که زوایای داخلی، مجموع کوچکتر از دوقائمه را تشکیل
میدهند یکدیگر را قطع میکنند.‘ ریاضیدانان متعجب بودند که آیا واقعاً این نوع
از پیچیدگی لازم بود یا نه. شاید بتوان وجود خطوط موازی را از بقیه اصول اقلیدس
نتیجه گرفت؟
آنها
توانستند صورتبندی (formulation) دست و پاگیر اقلیدس
را با فرضهای سادهتر و قابلفهمتری جایگزین کنند. شاید سادهترین آنها اصل توازی پلیفِر (Playfair's
axiom) باشد که میگوید: ’در یک صفحه، یک خط و نقطهای ناواقع
بر آن را داریم. از آن نقطه حداکثر یک خط میتوان رسم کرد که با خط داده شده موازی
باشد.‘ این
اصل بنام جان پلیفِر نامگذاری شده است که در سال 1795
آن را در کتاب اصول هندسه
خود بیان کرد. اگر بخواهیم دقیقتر بگوییم، او نیاز داشت تا حداکثر یک خط موازی
باشد.
...........................................
برای مطالعه ادامه این فصل نسخه کامل PDF کتاب را تهیه کنید.
اعدا صحیح
تا ابد ادامه دارند. هیچ عدد صحیحی وجود ندارد که از بقیه بزرگتر باشد، زیرا اگر
چنین چیزی وجود داشت، شما میتوانستید با اضافه کردن 1 به آن، عددی را بسازید که از
قبلی بزرگتر بود.
بیشتر
اعداد صحیح بزرگتر از آن هستند که شما بتوانید آنها را بر روی کاغذ بنویسید،
تفاوتی هم نمیکند که برای نوشتن آنها از چه دستگاه عدد نویسی استفاده کنید.
البته شما
همیشه میتوانید تقلب کنید، و از علامت a برای نشان دادن
بزرگترین عددی استفاده کنید که قابل تصور است.
ولی این
یک دستگاه نیست، فقط یک علامت تکی است.
خوشبختانه
ما به ندرت به اعداد بزرگ نیاز داریم.
ولی آنها شگفتیهای
خاصِ خودشان را دارند. و برخی اوقات یکی از آنها در ریاضیات اهمیت پیدا میکنند.
فاکتوریل (Factorial)
تعداد راههای مختلف چیدن اشیاء است.
به چند
طریق مختلف میتوان لیستی از چیزها را مرتب کرد؟ اگر لیست مورد نظر، مثلاً حاوی دو
حرف A و B
باشد، به دو طریق میتوان آنها را
مرتب کرد:
AB
BA
اگر لیست
حاوی سه حرف A،
B، و C باشد، شش راه برای اینکار
وجود دارد:
ABC ACB BAC BCA CAB CBA
اگر لیست
حاوی چهار حرف A،
B، C، و D باشد چطور؟
شما میتوانید
همه حالتهای ممکن را بصورت مرتب بنویسید، و با اینکار معلوم میشود که جواب 24 است. روش هوشمندانهای وجود دارد که با استفاده از آن میتوانید درستی این
مسئله را ثابت کنید. به این فکر کنید که D در کجاها ظاهر میشود. D یا باید در
مکان اول قرار گیرد، یا دوم، یا سوم، و یا چهارم. در هر حالت، فرض کنید D را برداریم.
آنگاه شما لیستی را خواهید داشت که فقط در آن A، B، و C قرار دارند؛ و این باید یکی
از شش حالت فوق باشد. همه شش حالت میتوانند وجود داشته باشند، فقط D را در مکان درست قرار دهید.
بنابراین ما میتوانیم کلیه حالتها را به صورت مجموعهای از چهار لیست از شش
چیدمان بنویسیم، مانند زیر:
D
در مکان اول قرار دارد:
DABC
DACB DBAC DBCA DCAB DCBA
D
در مکان دوم قرار دارد:
ADBC
ADCB BDAC BDCA CDAB CDBA
D
در مکان سوم قرار دارد:
ABDC
ACDB BADC BCDA CADB CBDA
D
در مکان چهارم قرار دارد:
ABCD
ACBD BACD BCAD CABD CBAD
کلیه این
چیدمانها متفاوت هستند، زیرا در هر یک از آنها D در مکان متفاوتی قرار دارد،
یا اینکه D در یکجا قرار دارد
ولی چیدمانهایABC با هم متفاوتند. بعلاوه، همه چیدمانهای ABCD
ظاهر میشوند: جایگاه D به ما میگوید
که به کدام مجموعه ششتایی نگاه میکنیم، و هنگامی که D برداشته شد، این به ما میگوید
کدام یک از چیدمانهای ABC
را انتخاب کنیم.
بدلیل
اینکه ما چهار مجموعه چیدمان داریم، که هر یک شش حالت دارند، تعداد چیدمانها روی
هم رفته برابر خواهد بود با 6×4=24.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
در سال
1974 مخترع مجارستانی ِارنو روبیک (Ernő Rubik)
یک بازی را اختراع کرد که از مکعبهای متحرک تشکیل شده بودند. حالا این بازی مکعب روبیک (Rubik
cube) نامیده میشود، و بیش از 350 میلیون نسخه از
آن در سراسر جهان به فروش رفته است. من هنوز بخاطر دارم که در آن سالها گروه ریاضی
دانشگاه ما چند کارتن از آنها را از مجارستان وارد کرده بود. عنوان این فصل،
تعدادِ حالتهای مکعب روبیک را نشان میدهد.
معما از یک مکعب تشکیل شده، که به 27
مکعب کوچکتر تقسیم شده. هواداران این بازی به اینها مکعبچه (cubies)
میگویند. هر طرف مکعب به یک رنگ است. ایده هوشمندانه روبیک این بود که مکانیزمی
را طرح ریزی کرد که اجازه میداد هر وجه این مکعب بچرخد. چرخشهای مکرر باعث میشد
تا رنگ مکعبچهها با هم مخلوط شوند. هدف از بازی این بود که مکعبچهها به جایگاه
اولیه خودشان بازگردانده شوند تا دوباره هر وجهِ مکعب به یک رنگ درآید.

شکل 171. مکعب روبیک.
مکعبچه
مرکزی را نمیتوان دید، و در حقیقت این مکعب با مکانیزم زیرکانه روبیک جایگزین شده
است. مکعبچههایی که در مرکز یک وجه قرار دارند میچرخند ولی به یک وجه دیگر
انتقال پیدا نمیکنند، و رنگ آنها تغییر نمیکند. بنابراین، از این پس ما فرض میکنیم
که این شش مکعبچه حرکت نمیکنند، مگر برای چرخش. یعنی قرار دادن کل مکعب در جهت
جدیدی، بدون اینکه در واقع هیچ یک از وجهها چرخانده شوند، و تاثیر چندانی هم
ندارند.
مکعبچههایی
که میتوانند حرکت کنند بر دو نوع هستند: 8 مکعبچه گوشهای،
که در گوشهها قرار دارند، و 12 مکعبچه کناری، که در
وسط لبه یک مکعب قرار دارند.
اگر شما
رنگهایی که در این گوشهها و کنارهها قرار دارند را در هر حالت ممکن با یکدیگر با
مخلوط کنید، مثلاً با کندن برچسبهای رنگی و قرار آنها در مکانی متفاوت، تعداد
چیدمانهای مختلفی که این رنگها میتوانند داشته باشند عبارت است از:
519,024,039,293,878,272,000.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
در سال 2005 تَب بازی سودوکو (Sudoku)
جهان را فراگرفته بود، ولی سابقه این بازی به خیلی پیش از این باز میگردد. این
بازی نیاز دارد تا شما ارقام 1 تا 9 را در یک مربع 9 × 9 قرار دهید که به
زیرمربعهای کوچکتر
3 × 3 تقسیم شده است. هر سطر، ستون، یا زیرمربع،
باید حاوی یکی از این ارقام باشد. برخی از ارقام، توسط کسانی که معما را طرح میکنند،
از قبل نوشته شدهاند، و شما باید بقیه آنها را پیدا کنید. عدد فوق تعداد جدولهای
متمایز سودوکو را نشان میدهد، و ما در این فصل قصد داریم به چگونگی این عدد
بپردازیم.
شکل 173. سمت چپ: یک جدول سودوکو حل نشده. سمت راست:
حل شده آن.
تاریخ
سودوکو اغلب به کارهای اویلر در مورد مربعهای لاتین باز میگردد [به فصل 10 رجوع کنید]. یک جدول کامل سودوکو نوع خاصی از مربعهای
لاتین است، که این زیرمربعهای 3×3 قیود تازهای را به
آن میافزاید. هنگامی که روزنامه فرانسوی Le Siècle در سال 1892 از خوانندگان
خود خواست تا یک جدول جادویی را که برخی اعداد آن پاک شده بود حل کنند، جدول مشابهای
پدید آمد. پس از آن مجله La
France از مربعهای جادویی استفاده کرد که فقط حاوی اعداد 1
تا 9 بودند.
شاید
اعتبار شکل جدید سودوکو را باید به هوارد گرانز (Howard Garns)
داد. در سال 1986 شرکت ژاپنی نیکولی، جدول سودوکو را در ژاپن چاپ کرد. در ابتدا
نام این جدول به ژاپنی ’سوجی وا دوکوشین ده کاگیرو‘ بود که به معنی ’ارقام به این
محدودند که تنها یکبار ظاهر شوند‘، ولی بعداً نام آنرا sudoku گذاشتند. مجله تایمز در سال
2004 شروع به چاپ جداول سودوکو کرد، و در سال 2005 این بازی در سطح جهان فراگیر
شد.
عدد بزرگ 6,670,903,752,021,072,936,960
که عنوان این فصل را تشکیل میدهد تعداد جداولِ مختلفِ سودوکو را نشان میدهد.
تعداد مربعهای لاتین 9 × 9 تقریباً یک میلیون
بار بزرگتر است و برابر است با:
5,524,751,496,156,892,842,531,225,600
تعداد
جداول سودوکو بدون اینکه اثبات شود، در سال 2003 در گروه خبری rec.puzzle چاپ شد. در سال 2005 Bertram Felgenhauer و Frazer Jarvis با کمک کامپیوتر،
و با تکیه بر روی برخی از احکام محتمل ولی ثابت نشده، جزئیات این مسئله را نشان دادند. این روشها
شامل درک تقارنهای سودوکو است. هر جدول حل شدهِ سودوکو گروه تقارن خاص خودش را
دارد [به فصل 168 رجوع کنید]، و شامل تبدیلاتی است (تعویض سطرها و ستونها)
که جدول را تغییر نمیدهد. ولی چیزی که ساختار اصلی را تشکیل میدهد گروه تقارنِ
مجموعه همه جداول ممکن است: یعنی راههای تبدیل هر جدول به جدول دیگر (احتمالاً به
همان جدول، ولی نه الزاماً).
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب
را تهیه کنید.
بزرگترین
عدد اول چیست؟ در قرن چهارم پیش از میلاد، اقلیدس ثابت کرد که چنین عددی وجود
ندارد. او میگفت: ’اعداد اول بیش از هر تعداد کثیری هستند.‘ یعنی، تعداد بینهایتی
از اعداد اول وجود دارند. کامپیوترها فهرست اعداد اول را بطور قابل ملاحظهای
افزایش دادهاند؛ و چیزی که در این راه مانع ادامه کار آنها بوده، نداشتن حافظه
کافی، یا کمبود کاغذ برای چاپ اعداد بوده است! در حال حاضر، عدد بالا رکورد
بزرگترین عدد اولی که ما میشناسیم را دارد.
چند سالی
است که در حوزه نظریه اعداد یک کار جدید مُد شده، و آن پیدا کردن بزرگترین عدد اول
است. این تلاش عمدتاً فقط برای شکستن رکوردهای قبلی، و یا محک زدن قدرت کامپیوترهای
جدید است. در آوریل 2014 بزرگترین عدد اول شناخته شده 257,885,161-1
بود، که تعداد ارقام آن به 17,425,170 رقم بالغ میشود.
اعدادی که
بصورت Mn=2n-1 هستند، به افتخار کاشف
فرانسوی آنها، مارین مرسن، اعداد مرسن (Mersenne
numbers) نامیده میشوند. اگر شما بدنبال شکستن رکورد اعداد اول
بزرگ هستید، اعداد مرسن نقطه شروع خوبی برای اینکار هستند، زیرا حتی اگر این اعداد
آنقدر بزرگ باشند که نتوان با روشهای عمومی با آنها کار کرد، آنها دارای ویژگیهایی
هستند که با استفاده از آنها میتوان اول بودن این اعداد را محک زد.
با کاربرد
یک روش جبری ساده میتوان ثابت کرد که اگر 2n-1
اول باشد، آنگاه n باید اول باشد. ریاضیدانان پیشین این تصور را داشتنند که عکس این نیز صادق
است، یعنی Mn
هنگامی اول است که n
اول باشد. ولی در سال 1536 Hudalricus
Regius متوجه شد که گرچه 11 اول است، ولی M11=2047
اول نیست. در واقع،
211-1=2047=23×89
Pietro Cataldi نشان داد که M17 و M19
اول هستند، کاری که با کامپیوترهای امروزی بسادگی میتوان آن را بررسی کرد، ولی در
زمانی که همه کارها با دست انجام میشد، این کار بسیار سخت بود. او همچنین ادعا کرد اگر n=23, 29, 31 و 37 باشد، Mn اول است. ولی،
M23
= 8,388,607 = 47 × 178,481
M29
= 536,870,911 = 233 × 1103 × 2089
M37
= 137,438,953,471 = 223 × 616,318,177
بنابراین
این سه عددِ مرسن همگی مرکب هستند. فرما در سال 1640 توانست M23 و M37 را تجزیه کند، و اویلر در سال 1738 M29 را تجزیه کرد. بعداً اویلر اثبات کرد که M31
اول است.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
همانطور
که قبلاً گفتم، ریاضیدانان بدلیل اینکه کاری غیرممکن بنظر میرسد، هیچ موقع از
انجام آن دست نمیکشند. اگر آن کار به اندازه کافی جالب باشد، آنها راهی برای ممکن
ساختن آن پیدا میکنند.
چیزی بنام
بزرگترین عدد صحیح وجود ندارد.
همه میدانند
که این اعداد تا ابد ادامه دارند.
ولی هنگامی
که جورج کانتور تصمیم گرفت این سؤال را مطرح کند که این مفهوم بااصطلاح’تا ابد‘
چه اندازه بزرگ است، او به روش بدیعی دست یافت که میشد از آن برای معقول کردن
اعداد بینهایت بزرگ استفاده کرد. یکی از پیامدهای آن این بود که برخی از بینهایتها
از بقیه بزرگتر هستند.
خیلی از
همعصران وی او را دیوانه میپنداشتند. ولی در دیوانگی کانتور روشی وجود داشت، و
معلوم شد که اعداد فرامتناهي او قابل درک و مهم هستند.
تنها کاری
که باید انجام دهید این است که به آنها عادت کنید. ولی این کار سادهای نبود.
ریاضیدانان
بدون هیچ قید و بندی، و به وفور از لغت ’بینهایت‘ (infinity)
استفاده میکنند. بصورت غیر رسمی، اگر شما نتوانید بزرگی چیزی را با اعداد صحیح
بشمارید، یا طول آن را با اعداد حقیقی اندازه بگیرید، بزرگی آن را بینهایت میپندارید.
در غیاب اعداد معمولی، ما از ’بینهایت‘ بعنوان یک جانگهدار (placeholder)
استفاده میکنیم. در مفهوم عادی، بینهایت یک عدد نیست. بینهایت چیزی است که
بزرگترین عدد ممکن میتواند باشد، اما بشرطی که عبارت فوق از نظر منطقی معنی بدهد.
ولی اکثر اوقات چنین چیزی منطقی نیست، مگر اینکه شما در مورد آنچه مورد نظرتان است
خیلی خیلی دقت کنید.
با شمارش
مجموعههای نامتناهی، کانتور راهی را پیدا کرد که بینهایت را به یک عددِ خاص تبدیل
میکرد. او با بکارگیری ایدههایش بر روی مجموعه کلیه اعداد صحیح، یک عدد نامتناهی به نام À0 (الف-صفر[10]
خوانده میشود) را تعریف کرد. این عدد از هر حدد صحیح دیگری بزرگتر است. پس آیا
این را باید بینهایت شمرد؟ خوب، تاحدی. مطمئناً این نوعی از بینهایت است.
در واقع باید گفت این کوچکترین بینهایت ممکن است. بینهایتهای دیگری نیز وجود
دارند، ولی آنها نسبت به الف-صفر بزرگتراند.
وقتی
کودکان شمردن را یادمیگیرند، و به اعداد بزرگی مثل هزار یا میلیون عادت میکنند،
غالباً این سؤال برایشان پیش میآید که بزرگترین عدد ممکن چه میتواند باشد. شاید
برخی از آنها فکر کنند که بزرگترین عدد چیزی شبیه به زیر باشد:
1,000,000,000,000,000
ولی سپس
آنها متوجه میشوند که با جایگزین کردن یکی از این 0ها با 1 میتوانند به عدد
بزرگتری دست پیدا کنند
1,000,000,000,000,001
هیچ عددِ
صحیحِ بخصوصی نمیتواند بزرگترین عدد باشد، زیرا با اضافه کردن 1 به آن، میتوانیم عدد بزرگتری داشته باشیم. اعداد صحیح تا ابد ادامه
دارند. اگر شروع به شمردن کنید و اینکار را ادامه دهید، شما به بزرگترین عددی نمیرسید
که در آنجا شمردن متوقف شود، زیرا چنین چیزی وجود ندارد. تعداد بینهایتی عدد وجود
دارد.
برای صدها
سال ریاضیدانان درمورد بینهایت بسیار محتاط بودند. حتی وقتی اقلیدس ثابت کرد که
تعداد بینهایتی از اعداد اول وجود دارند، او در بیان آن از لغت بینهایت استفاده
نکرد. تنها چیزی که گفت این بود ’تعداد اعداد اول بیش از هر تعداد کثیری هستند‘،
یعنی هیچ عدد اولی وجود ندارد که از بقیه بزرگتر باشد.
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
مهمترین
بصیرت کانتور این بود که نشان داد برخی از بینهایتها هستند که از بقیه بزرگترند.
او چیز مهمی بنام ’پیوستار‘ (continuum)
را کشف کرد، که نام پرطمطراقی برای دستگاه اعداد حقیقی است. کاردینال این مجموعه،
که آن را به c
نشان میدهند، از À0 بزرگتر است. برخی
اعداد گویا (درواقع بیشتر آنها) جزء اعداد صحیح نیستند، ولی اعداد صحیح و اعداد
گویا کاردینال یکسانی دارند، یعنی برای کاردینالهای نامتناهی، نیازی نیست تا به
قول گالیله ’کُل از جزء بزرگتر باشد‘. این به معنای آن است که شما نمیتوانید کلیه
اعداد حقیقی را، یک به یک، با همه اعداد صحیح متناظر کنید، حالا هر چقدر هم که
آنها را جابجا کنید باز هم تفاوتی نمیکند.
بدلیل
اینکه c
از À0 بزرگتر است، کانتور
میخواست بداند آیا در میان آنها کاردینالهای بینهایت دیگری نیز وجود دارند یا
نه. حدس پیوستار او میگوید که چنین چیزی وجود ندارد. او نه میتوانست این قضیه را
ثابت کند و نه میتوانست آن را رد کند. در سال 1940 کورت گودل، و
همچنین در 1963 پل کوهِن ثابت کردند که جواب هم ’بله‘ است هم ’نه‘. اینکه
جواب کدامیک از آنهاست، به این بستگی دارد که چگونه مبانی ریاضیات را پیریزی
کنید.
بخاطر
دارید که اعداد حقیقی را میتوان بصورت اعداد اعشاری نوشت که ارقام تناوبی دارند که بینهایت تکرار میشوند،
مثل 1.44444..، یا اعدادی مثل π که
بدون داشتن ارقام متناوب تا ابد ادامه دارند. کانتور متوجه شد (البته نه به شکلی
که من بیان میکنم) که مطمئناً بینهایتِ اعداد حقیقی از بینهایتِ اعداد شمارشی،
یعنی À0، بزرگتر است.
این ایده
بطور فریبندهای ساده است. در این استدلال از برهان خلف استفاده میشود. با امید
اینکه تناقضی را پیدا کنیم، فرض کنید که این امکان وجود دارد که اعداد حقیقی را با
اعداد شمارشی متناظر کرد. آنگاه ما فهرستی از اعداد اعشاری بینهایت رقمی را خواهیم
داشت که بصورت زیر هستند:
1$a0 a1a2a3a4a5...
2$bb1b2b3b4b5...
3$c0 c1 c2 c3
c4 c5...
4$d0 d1d2d3d4d5...
5$ e0 e1 e2 e3 e4 e5...
طوری که
هر عدد اعشاری نامتناهی جایی در سمت راست فهرست ظاهر شود. برای چند لحظه ارقامی که
بصورت پر رنگ چاپ شدهاند را نادیده بگیرید، من بعداً به سراغ آنها خواهم آمد.
ایده
درخشان کانتور این بود که یک عدد اعشاری بسازد که احتمالاً در فهرست فوق ظاهر
نشود. این عدد بصورت زیر است:
0x1x2x3x4x5...
که x1
با a1 متفاوت است
که x2
با b2 متفاوت است
که x3
با c3 متفاوت است
که x4
با d4 متفاوت است
که x5
با e5 متفاوت است
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
آیا
واقعاً 42
بیفایدهترین عددی است که وجود دارد؟
همانطور
که در مقدمه این کتاب اشاره کردم، در کتاب The Hitchhiker’s Guide to the Galaxy نوشته داگلاس آدامز، بطور آشکاری به عدد 42 اشاره میشود، و از آن بعنوان جواب ’پرسش بزرگ زندگی، جهان، و همه چیز‘ یاد
میشود. این سخن فوراً این سؤال جدید را پیش میآورد که اصلاً ’پرسش بزرگ زندگی،
جهان، و همه چیز‘ چه چیزی بوده؟ آدامز میگوید که او به این دلیل 42
را انتخاب کرد که یکی از دوستانش گفته بود این عدد واقعاً بیفایده است.
دراینجا
من قصد دارم از 42 در مقابل این بدنامی دفاع کنم. از نظر اهمیت ریاضی،
مسلماً 42 نسبت به اعدادی مثل 4 یا π، یا
حتی 17، در جایگاه بالاتری قرار نمیگیرد. ولی اینطور هم نیست
که بکلی بیفایده باشد. 42 یک عدد مستطیلی (pronic)، یک
عدد کاتالان (Catalan)، و یک ثابت جادویی
برای کوچکترین مکعب جادویی است. همچنین چند خاصیت دیگر نیز دارد.
یک عدد مستطیلی (یا عدد غیری)، عددی است که حاصل ضرب دو عدد صحیح متوالی
است. بنابراین شکل کلی این اعداد بصورت n(n+1) است. اگر n=6 باشد، خواهیم داشت 6 ×
7 =42. بدلیل اینکه nامین عدد مثلثی به صورت ![]() است، بنابراین یک عدد مستطیلی دو برابر یک عدد مثلثی
میباشد. و به همین جهت، مجموع n عدد زوج نخست نیز هست. تعداد نقاط به اندازه یک عدد مستطیلی را میتوان در یک
مستطیل مرتب کرد، که یکی از اضلاع به اندازه یک واحد از دیگری بزرگتر است.
است، بنابراین یک عدد مستطیلی دو برابر یک عدد مثلثی
میباشد. و به همین جهت، مجموع n عدد زوج نخست نیز هست. تعداد نقاط به اندازه یک عدد مستطیلی را میتوان در یک
مستطیل مرتب کرد، که یکی از اضلاع به اندازه یک واحد از دیگری بزرگتر است.

شکل 176. شش عدد مستطیلی نخست. سایهها نشان میدهند
که چرا هر یک دو برابر یک عدد مثلثی هستند.
حکایتی
هست که میگوید هنگامی که گاوس یک کودک دبستانی بود معلم کلاس برای دانش آموزان
مسئلهای را روی تخته نوشت:
1+2+3+4+…+100
گاوس
فوراً متوجه شد که اگر همان مجموع بصورت نزولی نوشته شود
100+99+98+97+…+1
...........................................
برای مطالعه ادامه این فصل نسخه کامل
PDF کتاب را تهیه کنید.
[1] - ”The Hitchhiker’s Guide to the Galaxy“ یا ”راهنمای مسافران کهکشان“، یک سری از کتابهایی هستند که توسط نویسنده انگلیسی داگلاس آدامز (2001-1952) (Douglas Adams) نوشته شدهاند (مترجم).
[2] - بابون (baboon) نوعی میمون است (مترجم).
[3]
- The important thing is not notations, but notions.
مهم نیست که اعداد را در چه دستگاهی و با چه علامتهایی نشان میدهیم، بلکه چیزی که
مهم است مفهوم خود عدد است (مترجم).
[4] - The Foundations of Arithmetic
[5] - Basic Laws of Arithmetic
[6]
-در اینجا برای بهتر رجوع کردن به نقشه از
املای لاتین ایالتها استفاده شده (مترجم).
[7]
- واژه اعشاری نیز از لغت عربی
عشر به معنای ده گرفته شده (مترجم).
[8]
- این عدد را با حرف φ ’ فی‘ یونانی، و برخی
اوقات نیز آن را با حرف τ ’تائو‘ نشان میدهند.
[9]
- در اینجا لغتهای کُد و رمز معنی یکسانی دارند و مشتقات آنها، مثل ’کدگذاری‘ و
’کدگشایی‘ با لغات ’رمزگذاری‘ و ’رمزگشایی‘، مترادف هستند و مطابق با سلیقه میتوان
از کُد بجای رمز یا برعكس استفاده کرد (مترجم).
[10]
- در زبانهای عربی، فارسی، و عبری ’الف‘ اولین حرف الفبا است. À
نشاندهنده عبری الف است (مترجم).