ترجمههای کامران بزرگزاد

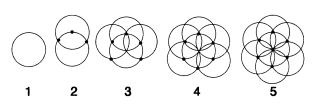
مروری بر تاریخ تقارن در
ریاضیات
جرلامو کاردانو دانشمند
قمار باز
روفینی،
واندرموند، و آبل طبیب بیچاره و بیمار نابغه
اواریست گالوا انقلابی
نگونبخت
وَنتزل و لیندمان
مهندس معمولی و استاد عالیمقام
سوفوس لی و کارل
کیلینگ، سرباز خیالباف و کتابخوان تنبل
آلبرت اینشتین کارمند
اداره ثبت اختراعات
ادوارد ویتن روزنامهنگار سیاسی
کتاب حاضر
ترجمهای است از ”Why beauty is truth?“
اثر ریاضیدان و مؤلف انگلیسی، یان استوارت (Ian Stewart).
وی در سال 1945 در انگلستان بدنیا آمد، مدرک کارشناسی خود را در رشته ریاضی از
دانشگاه کمبریج دریافت کرد، سپس در سال 1967 برای گرفتن دکترای خود به دانشگاه
واریک (Warwick) رفت، و از آن پس نیز در همین
دانشگاه مشغول تدریس و تحقیق بوده است.
استوارت
از جمله نویسندگانی است که به ترویج دانش علمی، و بالاخص ریاضیات، شهرت دارد. از
وی بیش 10 کتاب درسی، 20 کتاب عمومی غیر تخصصی، و بیش از صد و پنجاه مقاله منتشر
شده. سری کتابهای (Discworld)، که او با زیست شناس
مشهور، جک کوهن، نوشته بسیار معروف و پر فروش هستند.
درباره
کتاب
کتابِ
”چرا زیبایی واقعیت است؟“ از جمله کتابهای عمومی است که استوارت برای مخاطبین غیر
متخصص نگاشته. این کتاب به سرگذشت تقارن در ریاضیات میپردازد و گسترش تدریجی آنرا
از هزاره سوم قبل از میلاد تا قرن بیست و یکم مورد بررسی قرار میدهد. تقارن، که
بصورت نظریه گروهها در ریاضیات تجلی پیدا میکند، یکی از اساسیترین و جالبترین
مباحث مطرح در ریاضیات و فیزیک نوین است. آشنایی انسان با تقارن به ماقبلِ تاریخ
باز میگردد. ولی تنها در 170 سال گذشته بود که توانسته معیارهای قابل سنجشی برای
تقارن پیدا کند، کارهایی که در آغاز قرن نوزدهم توسط آبل و گالوا شروع شد، و در
اواخر همین قرن با کارهای لی و کیلینگ به بلوغ رسید. این روندی است که پس از گذشت
دو سده همچنان ادامه دارد. نام کتاب به دو چیز دلالت دارد، یکی زیبایی، و دیگری
واقعیت. معیار انسان برای زیبایی هر چیز، وجود نوعی تقارن در آن بوده؛ ما به چه
چیزی زیبا میگوییم؟ چه موجودی را زیبا میبینیم؟ دیر زمانیست که جواب این سئوالها
پیدا شده: مهمترین عامل برای زیبایی یک شئ یا یک انسان، و یا هر موجود دیگری،
تفاوت نمیکند، داشتن تقارن ظاهری در آن است. عموماً چیزهایی زیبا هستند که دارای
یک (یا چندین) تقارن باشند. اگر گلها زیبا هستند بخاطر وجود تقارن زیاد در
آنهاست. اگر انسانی زیبا بنظر میرسد، مطمئناً تقارن ظریفی در چهره و یا اندام او
وجود دارد. بنابراین یکی از اجزاء عنوان کتاب که به زیبایی دلالت دارد مستقیماً به
تقارن بازمیگردد.
جزء دوم
عنوان کتاب شامل واقعیت است. نویسنده سعی دارد با پیوند دادن واقعیت جهان فیزیکی
با مبحث تقارن، ثابت کند که زیبایی و واقعیت دو روی یک سکه هستند؛ اساسیترین وجوه
جهان از تقارن پیروی میکند؛ پس واقعیت زیباست، و زیبایی هم واقعیت است. برای
اینکه واقعیت جهانِ امروز بهتر شناخته شود، نویسنده در فصول پایانی کتاب به مباحثی
در فیزیک نوین و نظریه ذرات بنیادی میپردازد و مبحث تقارن را در آنجا دنبال میکند.
در
ریاضیات، تقارن ابتدا خود را بصورت مباحثی در جبر و حل معادلات نشان داد. خلاصه
مطلب این است که از حدود 400 سال قبل ریاضیدانان متوجه شدند که نمیتوان برخی از
معادلات را با ابزارهای عادی جبر حل کرد. اینکه چه معادلاتی را میتوان حل کرد، و
چه معادلاتی را نمیتوان، به تقارنهای موجود در آنها باز میگردد. بر همین اساس
این کتاب مروری دارد بر روشهای حل معادلات از 4000 سال قبل تا به امروز. البته
همانطور که خود نویسنده اشاره میکند، بمنظور اینکه کتاب را برای طیف گستردهتری
قابل استفاده کند، در آن از کاربرد زبان ریاضیات و جبر بسیار پرهیز شده. شاید این
باعث شود تا کتاب از این نظر سادهتر بیاید. مباحث تاریخی/ فلسفی که در این کتاب
مطرح میشوند جای مطالب ریاضی را پر کرده و شاید از این نظر کتاب کمی پیشرفته
باشد، و برای مطالعه و درک بهتر آن، باید حوصله بیشتری بخرج داد.
کتاب مورد
استفاده چه کسانی است؟
مطالعه
این کتاب تقریباً هیچ پیش نیازی ندارد، و تنها چیزی که برای آن لازم است علاقه به
علم و دانش است. این کتاب میتواند مورد استفاده طیف وسیعی از افراد باشد:
دانشجویان و دانشآموزان رشتههای علمی، علاقهمندان به علوم خالص، خصوصاً ریاضیات
و فیزیک، و کسانی که به تاریخِ علم علاقه دارند. در زمینه کتابهای عامهفهم علمی
به زبان فارسی (مخصوصاً ریاضیات و فیزیک نوین)، کمبودهای زیادی هست، که امید آن میرود
ترجمه این کتاب توانسته باشد گوشهای از آن را پر کند.
دراینجا
لازم میدانم از پدرم، که بیست و اندی سال قبل از میان ما رفت، یاد کنم. فکر میکنم
کنجکاوی من نسبت به علم از او مایه گرفته. یادش همیشه گرامی. از آقایان مهندس علی
ذاکری و جمال هادیپور که در ترجمه این کتاب مشوق من بودهاند تشکر میکنم. و
نهایتاً از همسرم سودی، نه فقط بخاطر خواندن و اصلاح دست نوشتههایم، بلکه برای
اصلاح و غلطگیری تمام زندگیم، سپاسگزارم.
پاییز 1391
کامران بزرگزاد ایمانی
تاریخ 30
ماه می 1834 بود. در میان مه صبحگاهی، دو مرد فرانسوی، با تپانچههایی که روبه
پایین گرفته شده بود، برای دوئل بر سر یک زن در مقابل یکدیگر قرار گرفته بودند.
ناگهان تیری شلیک شد، یکی از دو مرد درحالی که بطور مهلکی زخمی شده بود بر روی
زمین افتاد. او روز بعد، درحالی که تنها 21 سال داشت، براثر جراحتی که برداشته بود
تلف، و در یک گور بینام و نشان دفن شد. با این حادثه نزدیک بود یکی از مهمترین
ایدههای تاریخ ریاضیات نیز با او بخاک سپرده شود.
شخصی که
از دوئل جان سالم بدر برد ناشناخته ماند، ولی کسی که کشته شد اواریست گالوا[1]، یک انقلابی سیاسی و یک ریاضیدان وسواسی بود، که مجموع آثار او
به سختی از شصت صفحه تجاوز میکرد. بااینحال گالوا از خود میراثی بجا گذاشت که
ریاضیات را دگرگون کرد. او زبانی را اختراع کرد که میتوانست تقارنِ ساختارهای
ریاضی را توصیف، و پیامدهای آنرا نتیجهگیری کند.
امروزه آن
زبان به ”نظریه گروهها“ شناخته میشود و هم در ریاضیات محض و هم در ریاضیات
کاربردی، و کلاً در هر جایی از جهان که صحبت شکل گیری الگوها باشد، از آن استفاده
میشود. مبحث تقارن و گروهها همچنین در پیشرفتهترین مباحث فیزیک، یعنی در دنیای
فوقالعاده کوچک نظریه کوانتوم، و دنیای بسیار بزرگ نظریه نسبیت نقش محوری دارد،
نقشی چنان اساسی که حتی ممکن است راهی باشد بسوی نوعی از ”نظریه همه چیز[2]“، یعنی نظریه وحدت بخش ریاضی که میتواند این دو حوزه کلیدی
فیزیک را با یکدیگر متحد کند. با اینحال، این مبحث از یک سئوال ساده جبر شروع شد،
و آن این بود: ”چگونه میتوان جوابهای یک معادله جبری را پیدا کرد؟“.
تقارن، یک
عدد، و یا یک شکل نیست، بلکه حالت بخصوصی از یک تبدیل[3] است (روشی برای حرکت دادن یک شئ). اگر
شئ مورد نظر پس از تبدیل مانند قبل بنظر برسد، آنگاه تبدیل مورد نظر یک تقارن است.
برای مثال یک مربع هنگامی که 90 درجه چرخانده شود باز هم مثل قبل خواهد بود.
این ایده،
که امروزه بصورت گستردهای بسط داده شده و پیراسته گردیده، برای فهم جهان و منشاء
آن از اهمیت بنیادی برخوردار است. در بطن نظریه نسبیت اینشتین، اصلی نهفته که میگوید
قوانین فیزیک باید در همه مکانها و در همه زمانها یکسان باشد. این بدین معنی است
که قوانین باید نسبت به حرکت در فضا، و گذشت زمان، متقارن باشند. فیزیک کوانتوم به
ما میگوید که همه چیز در جهان از مجموعه ذرات بسیار ریزی به نام ”ذرات بنیادی“
تشکیل شده است. رفتار این ذرات بوسیله معادلات ریاضی ”یا همان قوانین طبیعت“ تعیین
میشوند، که خود این قوانین خاصیت تقارنی دارند. از نظر ریاضی، ذرات میتوانند به
ذرات متفاوتی تبدیل شوند، و خود این تبدیلات نیز قوانین فیزیک را بدون تغییر باقی
خواهند گذاشت.
این
مفاهیم، به همراه مباحث پیشرفتهتری که امروزه در فیزیک مطرح است، نمیتوانسته
بدون درک عمیق ریاضی از تقارن حاصل شود. این درک ابتدا از ریاضیات محض سرچشمه
گرفت، ولی در فصلهای آتی به نقش آن در فیزیک اشاره خواهیم داشت. برخی اوقات
مفیدترین ایدهها میتوانند از ملاحظاتی کاملاً انتزاعی حاصل شوند، چیزی که
فیزیکدان آمریکایی یوجین وینگر از آن بعنوان ”تاثیر بیاندازه ریاضیات در
علوم طبیعی“ اشاره میکند. هنگامی که از ریاضیات استفاده میکنیم، سود ما بیش از
آن است که انتظار میرود.
ما کتاب
خود را با کاتبین بابل قدیم آغاز خواهیم کرد و با مباحثی از فیزیک قرن بیست و یکم
به پایان خواهیم رساند. این کتاب به ما خواهد گفت که چگونه ریاضیات مفهوم تقارن را
کشف کرد، و چگونه یک جستجوی بظاهر بیفایده برای فرمولی که بعداً معلوم شد غیر
ممکن است، پنجرههایی را بسوی جهان گشود و موجب انقلابی در علم و ریاضیات گردید.
بصورت گستردهتر، داستان تقارن نشان خواهد داد که چگونه تاثیرات فرهنگی، و امتداد
تاریخیِ ایدههای بزرگ میتواند بوسیله تحولات گاه و بی گاه سیاسی و علمی برجسته
شود.

ممکن است
بنظر برسد که نیمه نخست کتاب هیچ ارتباطی با تقارن، و یا حتی کمترین ارتباتی با
جهان واقعی نداشته باشد. دلیل این امر این است که برخلاف نظر بسیاری، ایده تقارن
چیزی نیست که از هندسه حاصل شده باشد. در عوض، مفهوم فوقالعاده زیبا و ضروری
تقارن، که امروزه ریاضیدانان و فیزیکدانان از آن بهره میبرند از جبر منشاء گرفته.
بنابراین، بیشتر این کتاب روایتی خواهد بود در رابطه با جستجو برای حل معادلات
جبری. این رویکرد ممکن است فنی بنظر برسد، ولی جستجوی ما بسیار جالب، و زندگی
بازیگران اصلی آن اغلب غیرعادی و مهیج است. گرچه اغلب ریاضیدانان در تفکرات
انتزاعی خود درگیرند، ولی بااینحال هنوز هم انسانند. برخی از آنان ممکن است
زیاد از حد در زندگی شخصی خود پیرو منطق باشند، ولی در این کتاب بارها خواهیم دید
که قهرمانان ما حقیقتاً میتوانند خیلی انسانتر از بقیه باشند. ما خواهیم دید که
آنها چگونه زندگی میکنند و چگونه میمیرند، از ماجراهای عشقی و دوئلها، دعواها،
رسواییهای جنسی، مستیها و بیماریهای آنها خواهیم گفت و درکنار اینها خواهیم دید
که چگونه ایدههای ریاضی آنها آشکار شد و جهان ما را تغییر داد.
ما روایت
خود را از قرن دهم پیش از میلاد شروع میکنیم. روایتی گام به گام برای غلبه
بر معادلات، که در اوایل قرن نوزدهم با گالوا به اوج خود میرسد، روندی که سرانجام
در مواجه با معادلات درجه پنجم با مانع روبرو میشود. آیا روشهای موجود بدلیل
اینکه معادلات درجه پنجم تفاوت اساسی با بقیه معادلات داشتند درهم میشکند؟ یا
شاید روشی قدرتمندتری برای فرمولبندی حل این نوع معادلات وجود دارد؟ آیا
ریاضیدانان در یک مانع اساسی گیر کرده بودند، و یا شاید فقط بیراهه میرفتند؟
مهم است بدانیم
که راه حلهایی برای حل معادلات درجه پنجم موجود بودند. ولی سئوال این بود که آیا
همیشه میتوان آنها را بصورت یک فرمول جبری نمایش داد؟ در سال 1821 ریاضیدان جوان
نروژی نیلز هنریک آبل ثابت کرد که معادلات درجه پنجم را نمیتوان بوسیله فرمولهای
جبری حل کرد. ولی برهان او حالتی مبهم و غیر مستقیم داشت. این برهان اثبات میکرد
که هیچ راهحل عمومی امکانپذیر نیست، ولی حقیقتاً توضیح نمیداد که چرا.
این گالوا
بود که با استفاده از تقارن معادلات درجه پنجم، ناممکن بودن حل آنها را کشف کرد .
اگر آن تقارنها از آزمونی موسم به ”آزمون گالوا“ موفق بیرون میآمدند (یعنی به
حالت خاصی در کنار یکدیگر قرار میگرفتند، که من بعداً به آن اشاره میکنم) آنگاه
اینگونه معادلات میتوانستند بوسیله فرمولهای جبری حل شوند. اگر تقارنها در آزمون
گالوا موفق نمیشدند، آنگاه هیچ فرمولی برای حل آنها به طریقه جبری وجود نداشت.
معادلات
درجه پنجم در شکل عمومی خود نمیتوانند بوسیله فرمول حل شوند چون نوع تقارن آنها
مناسب نیست.

این کشف
حماسی، موضوع دوم این کتاب یعنی مبحث گروهها[4] (بعبارتی حسابان تقارن[5]) را تشکیل میدهد. گالوا از یک سنت
دیرینه ریاضی، یعنی جبر، پیروی کرد و بگونهای آنرا دوباره اختراع کرد تا بتوان
بعنوان ابزاری برای مطالعه تقارن از آن استفاده کرد.
فعلاً در
این مرحله ، عباراتی همچون ”گروهها“ اصطلاحاتی تعریف نشده هستند. هر زمان که
معنای آنها برای داستان ما اهمیتی پیدا کند من آنها را شرح خواهم داد. گاهی اوقات
ما برای ادامه راه خود نیاز داریم اصطلاحات مناسبی در چنته داشته باشیم. اگر به
عباراتی برخورد کردید که بنظر فنی میرسند، و بلافاصله تعریفی برای آنها ارائه
نشده، آنها را بعنوان برچسبهای مفیدی درنظر بگیرید که معنای واقعی آنها در مرحله
فعلی خیلی مهم نیست. برخی اوقات اگر به خواندن ادامه دهید، معنی این اصطلاحات خود
بخود آشکار میشود. اصطلاح ”گروه“ یکی از این موارد است، ولی ما تا اواسط کتاب به
معنای آن پی نخواهیم برد.
داستان ما
همچنین به اهمیت شگرف برخی از اعداد در ریاضیات اشاره خواهد داشت. منظور من از
عدد، ثابتهای بنیادی فیزیک نیست بلکه به ثابتهای ریاضی نظیر عدد پی (π) اشاره میکنم. برای مثال، در
اساس سرعت نور هر مقداری میتواند باشد، ولی از قرار معلوم در جهان ما این عدد
چیزی حدود 300.000 کیلومتر بر ثانیه است. از طرف دیگر عدد π کمی بیشتر از 3.14159 است، و
هیچ چیزی در جهان نمیتواند این مقدار را تغییر دهد.
حلناپذیری
معادلات درجه پنجم نیز این مسئله را به ما میگوید که 5 هم مثل π ، عددی بسیار غیر معمولی است.
5 کوچکترین عددی است که گروههای متقارن وابسته به آن در آزمون گالوا رد میشوند.
یک مثال نادر دیگر موردی است که در رابطه با سلسله اعداد 8 ,4 , 2, 1 وجود دارد.
ریاضیدانان یک سری از بسطهای اعداد ”حقیقی“ را کشف کردند که به اعداد مختلط منجر
شد و آنگاه این بسطها به چیزهای مثل کواترنیونها[6] (چهارگانها) و اوکتونیونها[7] (هشتگانها) ادامه یافت. این اعداد به ترتیب از حاصل ترکیب
دو، چهار، و هشت عدد حقیقی ساخته میشوند. بعد از اینها چه خواهد آمد؟ یک حدس
طبیعی 16 (شانزدهگان) است، ولی در حقیقت هیچ بسط قابل توجهِ دیگری از
دستگاه اعداد وجود ندارد. این واقعیتی است بس ژرف و قابل ملاحظه. این به ما میگوید
که چیز بخصوصی در رابطه با عدد 8 وجود دارد، آنهم نه از نظر ظاهری و سطحی، بلکه از
نظر ساختار بنیادین خود ریاضیات.
در کنار
اعداد 5 و 8، در این کتاب اعداد دیگری نیز ظاهر میشوند، که از مهمترین آنها
میتوان به 14, 52 , 78, 133 و 248 اشاره کرد. این اعداد
عجیب، ابعاد ”پنج گروه لیِ استثنائی[8]“ هستند که تاثیر آنها بر کل ریاضیات و بیشتر
فیزیک-ریاضی سایه افکنده. اینها شخصیتهای اصلی نمایشنامه ریاضی ما هستند، درحالی
که اعداد دیگر تنها بازیگران عادی بحساب میآیند.
ریاضیات
فقط هنگامی به خاصیت این اعداد پی برد که جبر مجرد[9] نوین در پایان قرن نوزدهم پا به عرصه وجود
نهاد. چیزی که مهم است خود این اعداد نیستند، بلکه نقشی است که در بنیاد جبر بر
عهده دارند. در ارتباط با هر یک از این اعداد، یک شئ ریاضی، با ویژگیها و خواص
منحصربفردی وجود دارد بنام ”گروه لی“[10] . این گروهها نقش مهمی را در فیزیک نوین
بازی میکنند، و آنگونه که معلوم شده ارتباط عمیقی با ساختار فضا، زمان و ماده
دارند.

این مورد
ما را به آخرین مبحث کتاب، یعنی فیزیک بنیادی، خواهد رساند. از قدیم فیزیکدانان
همیشه متعجب بودهاند که چرا فضا دارای سه، و زمان دارای یک بعد است – به عبارت
دیگر چرا ما در یک فضا-زمان چهار بعدی زندگی میکنیم. نظریه ابرریسمانها[11]، که آخرین تلاش ما برای متحد کردن کل فیزیک در قالب مجموعهای از قوانین
سازگار و منسجم است، فیزیکدانان را به سمتی سوق داده که فکر کنند فضا-زمان
ما ممکن است ابعاد پنهان دیگری را در خود داشته باشد. این موضوع ممکن است
مسخره بنظر برسد، ولی سوابق تاریخی خوبی برای آن موجود است. وجود چنین ابعاد اضافی
شاید کم چالشترین وجه نظریه ابرریسمانها باشد.
وجه دیگر
این نظریه، که بسیار بحثانگیز است، بر این باور است که فرمولبندی نظریه جدید فضا
و زمان عمدتاً به ریاضیات نظریه نسبیت و نظریه کوانتوم، یعنی دو رکن اساسی
که فیزیک نوین بر آنها بنا شده، بستگی دارد. بنظر میرسد متحد کردن این دو نظریه
کاملاً متضاد با یکدیگر، بیشتر یک روند ریاضی باشد تا یک روند فیزیکی که به
آزمایشات جدید و انقلابی نیاز دارد. انتظار میرود زیبایی ریاضی لازمه حقیقت
فیزیکی باشد. این میتواند فرض خطرناکی باشد. مهم است که هیچگاه چشمان خود را بر
روی جهان فیزیکی نبندیم، و هر نظریهای هم که عاقبت از کنکاشهای فکری امروز حاصل
شود، هر قدر هم بر ریاضیاتی قوی استوار باشد، نمیتوان آن را از مقایسه با مشاهدات
و آزمایشات مستثنی کرد.
ولی در
حالحاضر دلایل خوبی برای ادامه رویکرد ریاضی وجود دارد. یکی این است تا زمانی که
هنوز یک نظریه مرکب از این دو پیدا نشده، که حقیقتاً قانع کننده باشد، هیچ کس
نمیداند که چه آزمایشی را باید برای تائید آن انجام دهد. دلیل دیگر این است که
تقارن ریاضی نقشی اساسی هم در نظریه نسبیت و هم در نظریه کوانتوم دارا است، و
بدلیل اینکه نقاط مشترک این دو نظریه اندک است ما باید قدر این نقطه مشترک را
بدانیم و بر روی آن تکیه کنیم. ساختارهای مختلف فضا، زمان و ماده بوسیله تقارن
آنها حاصل میشود، و بنظر میرسد برخی از مهمترین شِقها با ساختارهای
استثنایی در جبر وابستهاند. ممکن است خواصی را که فضا-زمان دارا هستند از این جهت
باشد که ریاضیات تنها به فهرست خاصی از فرمها اجازه وجود میدهد. اگر چنین باشد
معقول بنظر میرسد تا رویکردی ریاضی داشت.
چرا بنظر
میرسد جهان اینقدر با ریاضیات گره خورده؟ پاسخهای مختلفی برای این سئوال پیشنهاد
شده، ولی من هیچ یک از آنها را قانعکننده ندیدهام. رابطه متقارن بین ایدههای
ریاضی و جهان واقعی، همانند تقارنی که بین حس زیبایی ما و مهمترین اشکال ریاضی
وجود دارد، معمایست بس ژرف و احتمالاً غیر قابل حل. هیچ یک از ما قادر نیست بگوید
که چرا زیبایی واقعیت است و واقعیت نیز زیباست. ما تنها میتوانیم به
ارتباطات پیچیده و بیشماری که آنها با یکدیگر دارند بیاندیشیم.
از میان
نواحی که امروزه عراق نامیده میشود، دو رود معروف جهان جاری هستند، و تمدنهای
برجستهای که از آنجا برخواستهاند، وجود خود را مدیون آنها میدانند. این دو رود
که از جبال شرقی ترکیه سرچشمه میگیرند از صدها کیلومتر اراضی حاصلخیز عبور کرده و
به آبراهی منتهی میشنود که دهانه آن به خلیج فارس باز میشود. این رودها از طرف
جنوب غربی به صحراهای خشک فلات عربستان، از شمال شرقی به مناطق غیر قابل سکونت
سلسله جبال آنتی-تاروس و کوهای زاگرس محدود هستند. نام این رودها دجله و فرات است
و چهار هزار سال قبل نیز همین مسیری را طی میکردند که حالا طی میکنند، با این
تفاوت که بجای عراق کنونی، نام این سرزمینهای باستانی آشور، اکد و سومر بود.
از نظر
باستان شناسان آن نواحی که بین دجله و فرات بودند به بینالنهرین، یا ”میان رودان“
شناخته میشود. معمولاً از این نواحی (بحق) بعنوان مهد تمدن یاد میشود. رودها با
خود آب را به جلگهها میآوردند و این آب خود موجب حاصل خیزی جلگهها میشود. وفور
زندگی گیاهی موجب جذب گلههای گوسفند و آهو میشد، که آنهم به نوبه خود موجب جذب
شکارچیان میگردید. از جمله این شکارچیان انسان بود. جلگههای بینالنهرین بهشتی
برای شکارچیان، و همینطور جاذبهای برای قبایل بادیه نشین بود.
در حقیقت
این نواحی چنان حاصلخیز بود که سرانجام موجب شد تا سبک زندگی شکارچیان منسوخ شده و
راه برای روشهای موثرتر تحصیل غذا باز شود. در حدود نه هزار سال قبل از میلاد، در
تپههای مجاور حلال حاصلخیز ما، کمی بسمت شمال، جهان شاهد ظهور یک فناوری انقلابی
بود: کشاورزی. پس از آن دو تغییر مهم در جوامع بشری رخ داد: نیاز به ماندن در یک
مکان برای مراقبت از محصولات، و امکان غذا دادن به تعداد زیادی از انسانها. این
ترکیب منجر به احداث شهرهایی شد که هنوز میتوان در بینالنهرین خرابههای باستانی
آنها را پیدا کرد، دولت-شهرهایی نظیر: نینوا[12]، نیمرود، نیپور، اوروک، لاگاش، ایردو، و بالاتر از همه، سرزمین
باغهای معلقه و برج معروف، یعنی شهر بابل[13] قرار داشت. در آنجا بود که چهار هزار سال قبل، بطور گریز ناپذیری
انقلاب کشاورزی موجب شد تا جوامع سازمان یافتهای، با تمام ساز و برگهای آن از
قبیل دولت، تشکیلات اداری و قدرت نظامی در آن بوجود آید. مابین سالهای 2000 ق.م و
500 ق.م، تمدنی که بعنوان ”تمدن بابلی“ از آن یاد میشود در کنارههای رود فرات
شکفته شد. این نام برگرفته از نام پایتخت آن سرزمین است، ولی در مفهوم کلی، اصطلاح
”بابلی“ شامل فرهنگ سومری و اکدی نیز میشود. در حقیقت، اولین جایی که بر ما
شناخته شده و به بابل اشاره میکند، لوحهای سفالی سارگنِ اکدی[14] است که تاریخ آن به حدود 2250 ق.م بازمیگردد، گرچه منشاء مردمان
بابل به دو یا سه هزار سال قبل از آن باز میگردد.
ما معلومات
کمی در باره منشاء ”تمدن“ (لغتی که لفظاً بمعنای سازمانی از انسانها است که در
جوامعی سکنی گزیدهاند) داریم. با این حال بنظر میرسد که بسیاری از جنبههای
زندگی کنونی خود را مدیون بابلیان باستان هستیم. بویژه آنها ستارهشناسان خُبرهای
بودند و دوازده صورتفلکی دایرهالبروج[15]، تقسیم دایره به 360 درجه، تقسیم ساعت به
شصت دقیقه، و دقیقه به شصت ثانیه از ابداعات آنها بوده است. بابلیان برای کارهای
نجومی خود به چنین واحدهای اندازهگیری دقیقی نیاز داشتند، و از همین روی، در علمی
مهارت پیدا کردند که از دیرباز مستخدم نجوم بود. این علم چیزی نبود جز ریاضیات.
همچون ما،
آنها هم ریاضیات را در مدرسه یاد میگرفتند.
نابو[16] درحالی که بقچه نهاری را که مادرش برای او مهیا کرده در کنارش میگذاشت،
از همشاگردی خود سئوال کرد ”درس امروز چیست؟“
دوستش
گامیش با ترشرویی جواب داد ”ریاضی... نمیدانم چرا به جای آن قانون درس نمیدهند؟
من قانون خوب بلدم.“
نابو، که
ریاضیاتش خوب بود هیچگاه نمیتوانست بفهمد که چرا بقیه همشاگردیهایش این درس را
اینقدر مشکل میدیدند. ”گامش، بنظر تو نوشتن و حفظ کردن آنهمه عبارات مربوط به
قانون کسل کننده نیست؟“
گامش که
قدرتش در پُر-خوانی و داشتن یک حافظه خوب بود خندهای کرد و جواب داد ”نه خیلی هم
آسان است، چون مجبور نیستی فکر کنی.“
نابو جواب
داد ”دقیقاً به همین خاطر است که من فکر میکنم این کسالت آور است، درحالی که ریاضی...“
در همین حین، هومبابا، یکی دیگر از دوستانش که مثل همیشه دیر رسیده بود لوحش را
نشان داد و گفت ”نابو، من باید با این چکار کنم؟“ او به یک تکلیف ریاضی
اشاره کرد و گفت ”من یک عدد را در خوش ضرب کردم و حاصلاش را با دو برابر آن عدد
جمع کردم، نتیجه شده عدد 24. آن عدد چه بوده؟“
نابو پاسخ
داد ”چهار “.
گامش گفت
”راست میگویی؟“
هومبابا
گفت ”خوم هم میدانم، ولی چطور آنرا بدست آوردی؟“
نابو
با سعی فراوان همشاگردیهای خود را به یاد روشی که استاد هفته قبل یاد داده
بود انداخت: ”نصف عدد 2 را با 24 جمع کن، حاصل میشود 25. جذر آنرا بگیر میشود 5
...“
گامش
درحالیکه با ناراحتی دستهایش را تکان میداد گفت ”نابو، من واقعاً چیزی از جذر
نفهمیدهام.“
نابو گفت
”آهان میدانستم، “. انگار که او دیوانه شده، دو دستش نگاهی به او انداختند. نابو
ادامه داد ” حالا ما به یک جایی رسیدیم! گامش، مشکل تو حل معادلات نیست، بلکه جذر
گرفتن است!“
گامش زیر
لب گفت ”هر دو است،“
”ولی جذر
گرفتن اول میآید. همانطور که بارها استاد گفته، تو باید هر موضوعی را در جای خودش
و پله به پله یاد بگیری.“
هومبابا
با اعتراض گفت ”در ضمن او همیشه به ما گفته که لباسهای خودمان را هم کثیف نکنیم،
ولی ما هیچ وقت ...“
نابو گفت
”این مسئله فرق میکند. این ...“
گامش حرف او را قطع کرد و گفت ”این اصلاً خوب نیست،
من هیچ وقت یک کاتب نمیشوم و پدرم آنقدر مرا شلاق میزند که نتوانم بنشینم و مادرم
به من ملتمسانه نگاه خواهد کرد و میگوید باید بیشتر تلاش کنم و اینکه بفکر
خانواده باشم . ولی من نمیتوانم ریاضی را در مُخم فرو کنم! قانون! این چیزیست که من میتوانم آنرا حفظ
کنم. اینکار بامزه هم
هست! منظورم این است که فرض کنید زن یک مردی، بخاطر رابطه با مرد دیگری، شوهر خود
را میکشد. آیا باید زن را به چهار میخ کشاند؟ من میگویم این مسائل چیزهایست که
ارزش یادگرفتن دارند، نه چیزهای بی خاصیتی مثل جذر گرفتن.“ او درحالی که مکث کرد تا نفسش تازه شود، و
در حالیکه دستهایش از روی احساس میلرزیدند ادامه داد ”معادلات، اعداد – چرا باید سر
خودمان را با اینها درد بیاوریم؟“
هومبابا
جواب داد ”برای اینکه اینها مفیدند، آیا همه آن قوانینی که در مورد قطع گوش یک
برده بود بخاطر داری؟“
گامیش گفت
”آری! بحث کیفر حمله به یک نفر“
هومبابا سریع گفت ” و اگر چشم یک مرد عادی را کور
کردی باید به او … “
گامیش گفت
”یک سکه نقره بدهی“
”و اگر
استخوان یک برده را بشکنی؟“
”باید نصف
قیمت برده را بعنوان قرامت به صاحبش بپردازی.“
هومبابا
از جا پرید و گفت ”خوب پس اگر قیمت یک برده شصت شِکِل[17] باشد، تو باید بتوانی نصف شصت را حساب کنی. اگر
بخواهی در کار قانون باشی به ریاضی نیاز خواهی داشت!“
گامیش
فوراً جواب داد ”جواب سی است.“
نابو
فریاد زد ”ببین! تو میتوانی!“
حقوقدان
آینده درحالی که دستان خود را در هوا تکان میداد، و در جستجوی راهی بود تا عمق
احساسش را بیان کند گفت ”معلوم است که ما برای اینکار به ریاضی نیازی نداریم. اگر
موضوع بر سر جهان واقعی باشد، بله، من میتوانم ریاضی کار کنم. ولی نه مسائل غیر
واقعی مثل جذر گرفتن.“
هومبابا
گفت ”برای اندازهگیری زمین هم به جذر گرفتن نیاز داری.“
گامش جواب
داد ”بله درست است، ولی من درس نمیخوانم تا مامور جمع آوری مالیات از مالکان زمین
شوم، بلکه همانطور که پدرم خواسته، من هم میخواهم مانند او یک کاتب شوم. پس
نمیدانم که چرا باید اینهمه ریاضیات یادبگیرم.“
هومبابا
تکرار کرد ”برای اینکه مفید است“
نابو بهآرامی
گفت ”من فکر نمیکنم دلیل واقعی این باشد، بنظر من تمام اینها به زیبایی و حقیقت
ربط دارد، درباره گرفتن جواب مسائل است و دانستن اینکه آیا جوابی که میگیری درست
است یا نه.“ ولی نگاهی که بر چهره دوستانش نقش بسته بود نشان میداد که آنها
از این حرف او قانع نشدهاند.
گامش آهی
کشید و گفت ”ریاضیات برای من فقط در حکم بدست آوردن جواب مسئله است.“
نابو بر
حرف خود پافشاری کرد و گفت ”ریاضیات اهمیت دارد چون زیبا و صحیح است، جذر گرفتن
برای حل معادلات اساسی است، شاید خیلی کاربرد دیگری نداشته باشند، ولی این مهم
نیست. ریاضیات برای خودش اهمیت دارد.“
گامش که نزدیک
بود حرف بیربطی از دهانش خارج شود با دیدن معلم که به کلاس وارد میشود شرمندگی
خود را با چند سرفه پنهان کرد.
معلم با
خوش روی گفت ”صبح بخیر بچهها.“
”صبح بخیر
استاد،“
”خوب
بگذارید تکالیفتان را ببینم.“
گامش آهی
کشید. هومبابا مضطرب بنظر میرسید. نابو چهرهاش را بصورت بیاحساسی درآورد، چون
اینطور بهتر بود.
جدا از
خیالی بودن گفتگویی که ما مشغول استراقسمع آن بودیم، شاید
حیرت انگیزترین چیزی که در مورد آن وجود دارد اینست که مربوط به حدود 1100 ق.م است
و در شهر معروف بابل اتفاق میافتد.
منظورم
این است که ممکن است چنین گفتگوهای رخ داده باشد. در تاریخ هیچ سندی مبنی بر وجود
سه پسر به نامهای نابو، گامش و هومبابا وجود ندارد، چه رسد گفتگوی میان آنها. ولی
طبیعت انسان همان است که هزاران سال قبل بوده و داستان من در مورد این سه شاگرد بر
اساس حقایق محکمی بنا شده.
ما حقایق
زیادی در مورد فرهنگ بابلی میدانیم و دلیل آن این است که آنها بسیاری از مطالبشان
را با خط سوزنی شکل و عجیبی، که به خط میخی معروف است، بر روی لوحهای رُسی مینوشتند.
وقتی خاک رس زیر آفتاب خشک میشد این کتیبهها سفت شده، و تقریباً بصورت خراب
نشدنی در میآمدند. و اگر محل نگهداری این کتیبهها آتش میگرفت، همانطور که اغلب
چنین میشد، آتش موجب میشد تا این کتیبههای رُسی به سفال تبدیل شوند، که دوامشان
به مراتب بیشتر بود.
و نهایتاً
یک لایه پوششی از شنهای صحرا موجب میشد که این کتیبهها تا ابد محفوظ بمانند. به
همین دلیل است که بعد از گذشت چند هزار سال، هنوز هم بقیای این کتیبهها برای ما
باقی مانده تا بتوانیم تاریخ را از روی آنها استخراج کنیم. داستان فهم بشر از
تقارن از همین زمان آغاز گردید، تقارنی که تجسم سازمانیافته و کمّی آن بصورت نوعی
از ”حسابان“[18]، که از نظر قدرت از آنی که نیوتون و لایپنیتز ابداع کردند چیزی
کم ندارد. بدون شک اگر ما یک ماشین زمان، و یا حتی کتیبههایی قدیمیتر از آنچه
یافتهایم، در دست داشتیم، آنگاه میتوانستیم ردپای تقارن را در زمانهای بازهم
دورتری پیدا کنیم. ولی تا آنجا که تاریخ ثبت شده موجود به ما میگوید، این ریاضیات
بابلی بود که انسان را در مسیر تقارن قرار داد، آنهم با آن الزامات برجستهاش در
مورد چگونگی بینش ما از جهان.
ریاضیات
بر اعداد تکیه دارد ولی محدود به آنها نیست. بابلیها نوع سیستم نمایش اعداد را در
دست داشتند که بر خلاف عدد نویسی ما که در مبنای 10 است، بر مبنای ”شصت“ بود (یعنی
بجای توانهای 10، بر پایه توانهای 60 قرار داشت). آنها با مثلثهای قائمالزاویه
آشنا بودند و برای اندازهگیری آنها از چیزی شبیه به قضیه فیثاغورث استفاده میکردند
(گرچه برعکس اخلاف یونانی خود، ریاضیدانان بابلی علاقهای به اثبات یافتههای خود
با دلایل منطقی نداشتند). آنها از ریاضیات برای نجوم، کشاورزی، امور مذهبی، و
همچنین امور روزمرهای از قبیل تجارت و مالیات استفاده میکردند. این نقش دوگانه
ریاضیات (آشکار سازی نظم جهان و یاری رساندن به امور دنیوی انسان) همیشه همچون
ریسمانی طلایی در طول تاریخ کشیده شده است.
چیزی که
در مورد ریاضیدانان بابلی از اهمیت فراوانی برخوردار است اینست که آنها شروع به
فهم این مسئله کردند که چگونه باید معادلات را حل کرد.
معادلات
روشی هستند که ریاضیدانان برای یافتن کمیتی مجهول از روی مقادیری معلوم بکار میبرند.
معادلات همیشه به چنین شکلی مطرح میشوند: ”این معلومات در مورد عدد مجهول وجود
دارد: مقدار آنرا با توجه به این معلومات نتیجه بگیر.“ پس یک معادله بیشتر
شبیه یک معماست که روی یافتن یک عدد تمرکز دارد. به ما گفته نمیشود که آن عدد
چیست، ولی چیزهای مفیدی درباره آن در اختیار ما قرار میگیرد. وظیفه ما این است که
معما را با یافتن آن عدد حل کنیم. ممکن است بنظر رسد این بازی از مفهوم هندسی
تقارن فاصله گرفته، ولی در ریاضیات، ایدههایی که در یک زمینه بخصوص کشف میشوند،
همیشه خود را در زمینههای دیگری آشکار میکنند. این بهمپیوستگی درونی است که به
ریاضیات قدرت عقلانی زیادی میدهد. به همین دلیل است که دستگاه اعدادی که بابلیها
بمنظور تجارت ابداع کردند میتوانست همچنین برای پیشبینی وضعیت سیارات و ثوابت
(ستارگان) بکار گرفته شود.
معمای ما
میتواند ساده باشد، مثلاً: ”دو برابر عددی میشود شصت، آن عدد کدام است؟“ دراینجا
شما لازم نیست نابغه باشید تا جواب عدد مجهول، ما را که 30 است، نتیجه بگیرید. یا
در مواقعی میتواند سختتر باشد: ”من یک عدد را در خودش ضرب کردم و 25 را به آن
افزودم. حاصل ده برابر آن عدد شد. بگو آن عدد چیست؟“ شما ممکن است با آزمون
وخطا به جواب صحیح، که 5 است، برسید، ولی آزمون و خطا روش کارآمدی برای بدست
آوردن جواب معماهای ما (یعنی حل معادلات) نیست. برای نمونه اگر در مثال قبلی ما
عدد 25 را به 23، یا به 26، تغییر داده بودیم چه میشد. بابلیهای باستان روش
آزمون و خطا را حقیر میشمردند، زیرا آنها راز عمیقتر و قویتری را میدانستند.
آنها قاعد (یا روش معینی) را میدانستند که قادر بود اینگونه معادلات را حل
کند. تا آنجا که ما میدانیم، آنها اولین مردمانی بودند که فهمیدند چنان قواعدی
وجود دارد.
بخشی از
جذابیتهای بابل از روایاتی ناشی میشود که در کُتب مقدس تورات و انجیل آمده. مثل
داستان دانیال در کُنام شیر، که در بابل و در زمان حکمرانی بختالنصر روی میدهد.
ولی در زمانهای بعد، بابل چنان در رمز راز فرو میرود، که گویی این اسم تنها یک
افسانه بوده و اصلاً وجود نداشته. این نظر تا حدود دویست سال قبل رایج بود.
برای
هزاران سال تپههای عجیبی جلگههای عراق را پوشانده بود. شوالیههایی که از جنگهای
صلیبی بازمیگشتند از میان این تپهها سوغاتهایی مثل آجرهای مزین و یا کتیبههایی
با خطاطی عجیب به ارمغان میآوردند. معلوم بود که این تپهها بقایای شهرهای قدیمی
هستند، ولی به غیر از اینها، چیز بیشتری معلوم نبود.
در سال
1811 کلادیوس ریچ[19] اولین کسی بود که بصورت علمی شروع به مطالعه
خرابههای عراق کرد. او در صد کیلومتری جنوب بغداد، در کنار رود فرات، مکانی را
یافت که بزودی معلوم شد باید شهر بابل باشد، و کارگرانی را برای حفاری خرابهها
استخدام کرد. یافتهها شامل آجر، لوحهایی با خط میخی، مهرهای استوانهای شکل
زیبایی که اگر روی گل رس کشیده میشدند حروف برجسته تولید میکردند، و نیز آثار
هنری که بقدری با عظمت بودند که آفریننده آنها هر که بود، باید در رده لئوناردو
داوینچی و میکلانژ قرار میگرفت.
اما
جالبتر از همه اینها لوحهای شکستهای به خط میخی بود که در سراسر شهر پراکنده شده
بود. ما خیلی خوششانس هستیم که باستانشناسان اولیه ارزش واقعی آنها را درک کردند
و آنها را در جای امنی نگاه داشتند. بعدها که رمز این خطوط شکسته شد، این لوحها
بدل به گنجینه گرانبهایی از اطلاعات در مورد زندگی و علایق بابلیها شد.
لوحها و
دیگر بقایا، به ما نشان میدهد که تاریخ کهن بینالنهرین طولانی و پیچیده، و شامل
بسیاری از فرهنگها و دولتها، بوده است. معمولاً رسم بر این بوده که از لفظ ”بابل“
برای رجوع به تمام این فرهنگها، و نیز فرهنگ بخصوصی که مرکز آن شهر بابل بوده،
استفاده میشود. ولی قلب فرهنگ بینالنهرینی بصورت پیوسته در حال تغییر بوده، بعضی
اوقات شهر بابل مورد توجه قرار میگرفت و گاهی هم از این دایره خارج میشد. باستان
شناسان تاریخ بابل را به دو دوره اصلی قدیم و جدید تقسیم میکنند. دوره بابل قدیم
از حدود سال 2000 ق.م شروع میشود و تا 1600 ق.م ادامه مییابد. دوره بابل جدید از
625 ق.م تا 539 ق.م میباشد[20]. مابین این دو دوره اصلی، و هنگامیکه بابل زیر
حکومت خارجیها بود، دورههای آشور قدیم، کاسیت، آشور میانه و آشور جدید قرار میگیرد.
علاوه براین ریاضیات بابلی به مدت پانصد سال، در دورهای که به نام سلوکی[21] معروف است، در سوریه به رشد خود ادامه داد.
فرهنگ
بابلی، خود بیش از اجتماعاتی که در آن فرهنگ رشد میکرد، پایدار بود و تقریباً
بمدت 1200 سال بدون تغییر ماند، گرچه بواسطه دگرگونیهای سیاسی آن زمان هر از
چندگاهی دچار اختلال میشد. بنابراین هر جنبه بخصوص از فرهنگ بابلی، به غیر از
رویدادهای تاریخی خاص، احتمالاً قبل از آنکه از نظر تاریخی به ثبت برسند بوجود
آمدهاند. به ویژ شواهدی هست مبنی بر این که برخی از شیوههای ریاضی، که اولین
سابقه آنها در حدود سال 600 ق.م به ثبت رسیده، از خیلی پیشتر وجود داشتهاند. به
همین دلیل شخصیت اصلی این فصل، که کاتبی است که من نام نابو شَمَش[22] را بر او گذاشتم، باید در حدود سالهای 1100 ق.م و در دوره بختالنصر
اول زندگی میکرده.
کلیه
شخصیتهایی که در ادامه داستانمان با آنها برخورد میکنیم، شخصیتهای حقیقی و
تاریخی هستند و سرگذشت تک تک آنها بصورت مستند ثبت شدهاند. ولی در میان حدود یک
میلیون لوح رُسی که از بابل باستان بجای ماندهاند هیچ مدرکی به غیر از وجود
شخصیتهای برجسته نظامی و یا سلطنتی موجود نیست. پس ما شخصیت نابو را با تقلیدی از
آنچه که احتمالاً زندگی روزمره بابلیان آن زمان بوده خلق میکنیم. از نظر تاریخی ما
هیچ اختراعی را به او نسبت نمیدهیم، ولی او به کلیه جنبههای دانش بابلی که نقشی
در داستان تقارن بازی میکند برخورد خواهد کرد. شواهد خوبی در دست است که همه
کاتبین بابلی دورههای آموزشی دشواری را طی میکردند که ریاضیات مهمترین مولفه آن
بود.
نام کاتب
فرضی ما، نابو شَمَش، ترکیب دو نام اصیل بابلی نابو، که خدای کتیبه، و شَمَش
خدای خورشید، است. در فرهنگ بابلی، غیر معمول نبود که افراد عادی نام خدایان را
برای فرزندان خود برگزینند، گرچه شاید اسمی که از نام دو خدا تشکیل میشد کمی
نامتعادل بود. به دلیل اینکه این بخش جنبه داستانی دارد، ما مجبوریم تا با نام
مشخصی از او نام ببریم تا اینکه مثلاً او را صرفاً ”کاتب“ بنامیم، و این نامی است
که ما برای او انتخاب کردیم.
هنگامی که
نابو-شَمَش بدنیا آمد پادشاه بابل بختالنصر اول، مهترین پادشاه از سلسله آیسین،
بود. او را نباید با پادشاه معروف دیگری که بارها از او در کتب مقدس یاد میشود
اشتباه گرفت. آن پادشاه بختالنصر دوم بود و در سالهای 605 ق.م تا 562 ق.م حکمرانی
میکرد.
نابو-شَمَش
در یک خانواده ”طبقه-بالای“ معمول آن زمان در شهر باستانی بابل بدنیا آمد. محل
تولد او نزدیک دروازه معروف اشتار[23] بود. اشتار دروازه ورودی شهر بود که با
کاشیها و آجرهای رنگی، در نقشهای تخیلی همچون گاو، شیر و حتی اژدها، مزین شده
بود. جادهای که به این دروازه منتهی میشد، با داشتن عرضی حدود 20 متر، شگفت
انگیز بود. نام این جاده به معنای ”نگذار دشمنان پیروز شوند“ بود. این نام، نامی
عادی برای خیابانهای اصلی بابل محسوب میشد. از این جاده بیشتر کاهنانی که میخواستند
برای شروع مراسم مزهبی از جلو مردوک[24] رژه بروند استفاده میکردند.
حالا
ببینیم نابو در مدرسه چه یاد میگرفت. برای هرکسی (البته بجز فیلسوفان، منطقدانان
و ریاضیدانان که همه آنها در تعریف مفاهیم وسواس دارند) یک عدد از رشتهای از ارقام
تشکیل میشود. بنابراین سال 2006 که من مشغول نوشتن این کتاب بودهام، از چهار رقم
تشکیل میشود. ولی علمای وسواسی این تعریف را قبول ندارند و به ما خواهند گفت که
رشتهای از ارقام به هیچ وجه یک عدد نیست، بلکه فقط عدد را برای ما نمایش میدهد،
آنهم بصورتی پیچیده. دستگاه اعشاری[25] خودمان، برای نشان دادن هر عدد، هر چقدر هم
که بزرگ باشد، از ده رقم (0 تا 9) استفاده میکند. بسط این دستگاه اعشاری به ما
اجازه نمایش اعداد بسیار کوچک را نیز میدهد. مهمتر از آن اجازه میدهد هر عدد اعشاری
را، با هر تقریبی که بخواهیم، نمایش دهیم. برای مثال، بر طبق بهترین برآوردها،
سرعت نورتقریباً برابر است با 299,792.458 کیلومتر در ثانیه.
ما چنان
با این دستگاه عدد نویسی خو گرفتهایم که فراموش میکنیم چقدر هوشمندانه طراحی شده
است. نکته کلیدی که این دستگاه بر پایه آن بنا شده این است: مقدار عددی هر رقم،
مثلاً 2، وابسته به جایگاه آن عدد نسبت به بقیه ارقام است. رقم 2، بدون در نظر
گرفتن اینکه کجا قرار گرفته ندارد، معنی خاص و ثابتی ندارد. در عدد ذکر شده
قبلی، که نشان دهنده سرعت نور بود، رقم ”2“ که قبل از ممیز (.) قرار دارد حقیقتاً
به معنای ”دو“ است. ولی در اولین رقم سمت چپی که ”2“ ظاهر شده به معنای ”دویست
هزار“ است و در عدد 2006، همین رقم 2 بمعنای ”دو هزار“ است.
اگر سیستم نوشتاری ما هم بر همین اساس بود که حروف
الفبا بر حسب موقعیتی که در کلمه دارند معنی پیدا میکردند، آنوقت وضعیت خواندن و
نوشتن ما بسیار دشوار میشد. برای نمونه تصور کنید که دو ”الف“ که در کلمه ”الفبا“
قرار دارند، بسته به موقعیتشان (حرف اول و پنجم) دارای دو صدای متفاوت بودند! ولی
عدد نویسی برپایه مکان چنان آسان و نیرومند است که تصور روش دیگری از عدد نویسی را
برای ما دشوار میکند.
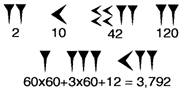
عدد نویسی بابلی در مبنای 60
![]() ولی همیشه همه چنین نبوده است. عدد نویسی به شکل امروزی آن تنها قدمتی 1500 ساله
دارد، و تنها حدود 800 سال است که این روش در اروپا مرسوم شده. ولی در فرهنگهای
باستانی اعداد به روشهای عجیبی نمایش داده میشدند. شاید معروفترین آنها دستگاه
عدد نویسی رومی باشد که در آن سال 2006 بصورت MMVI نمایش داده میشود. در یونان
باستان همین عدد بصورت نمایش داده میشد. به جای اعداد 2 ، 20 ، 200 و 2000
رومیها از نمادهای II, XX, CC
و MM استفاده میکردند.
یونانیان همین اعداد را با
ولی همیشه همه چنین نبوده است. عدد نویسی به شکل امروزی آن تنها قدمتی 1500 ساله
دارد، و تنها حدود 800 سال است که این روش در اروپا مرسوم شده. ولی در فرهنگهای
باستانی اعداد به روشهای عجیبی نمایش داده میشدند. شاید معروفترین آنها دستگاه
عدد نویسی رومی باشد که در آن سال 2006 بصورت MMVI نمایش داده میشود. در یونان
باستان همین عدد بصورت نمایش داده میشد. به جای اعداد 2 ، 20 ، 200 و 2000
رومیها از نمادهای II, XX, CC
و MM استفاده میکردند.
یونانیان همین اعداد را با 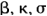 و
و
![]() نمایش
میدادند.
نمایش
میدادند.
بابلیها
جزء اولین فرهنگهای شناخته شدهای بودند که از چیزی شبیه به عددنویسی مکانی ما
استفاده میکردند. ولی یک تفاوت عمده وجود داشت. در دستگاه اعشاری وقتی یک رقم یک
قدم به سمت چپ حرکت میکند، مقدار عددی آن در 10 ضرب میشود. بنابراین 20 میشود
10 برابر 2، و 200 میشود 10 برابر 20. در سیستم بابلی هر حرکت بسمت چپ، عدد
را شصت برابر میکند. بنابراین ”20“ به معنی 2 برابر 60 است (که در مبنای ده
خودمان میشود 120) و ”200“ به معنای 2 ضرب در 60 ضرب در 60 (7200 در مبنای ده).
البته آنها از نشانهای شبیه به ”2“ یا ”0“ برای نوشتن اعداد استفاده نمیکردند،
بلکه مثلاً برای نوشتن ”دو“، با قرار دادن دو شکل میخی باریک (![]() )
پشت سر هم استفاده میکردند. همانطور که از شکل بالا پیداست اعداد بین یک تا نه،
با دستهبندی تعداد لازم از این حروف میخی نمایش داده میشود. برای نمایش ده از یک
هشتک کج شده (<)،
و برای نمایش بیست، سی، چهل و پنجاه از کنار هم قراردادن تعداد لازم از این هشتکها
استفاده میکردند. پس برای نمونه عدد ”42“ بوسیله چهار هشتک کج و دو میخ
باریک نمایش داده میشد (
)
پشت سر هم استفاده میکردند. همانطور که از شکل بالا پیداست اعداد بین یک تا نه،
با دستهبندی تعداد لازم از این حروف میخی نمایش داده میشود. برای نمایش ده از یک
هشتک کج شده (<)،
و برای نمایش بیست، سی، چهل و پنجاه از کنار هم قراردادن تعداد لازم از این هشتکها
استفاده میکردند. پس برای نمونه عدد ”42“ بوسیله چهار هشتک کج و دو میخ
باریک نمایش داده میشد (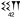 ).
).
به دلایلی
که درست نمیدانیم، این دستگاه عدد نویسی در 59 متوقف میشد. بابلیها به روش قبلی
شش هشتک را در کنار هم قرار نمیدادند تا از آن برای نمایش 60 استفاده کنند. درعوض
از یک میخ که برای نمایش ”یک“ از آن استفاده میشد، حالا برای نمایش ”یک شصت تایی“
نیز استفاده میکنند. دو میخ (![]() )
نماش دهنده ”دو شصتتایی“ یا همان 120 است. ولی دو میخ میتواند نشان دهنده 2 نیز
باشد. اینکه (
)
نماش دهنده ”دو شصتتایی“ یا همان 120 است. ولی دو میخ میتواند نشان دهنده 2 نیز
باشد. اینکه (![]() )
کدامیک از این دو عدد را نمایش میدهد باید از روی زمینه و موقعیت علائم نسبت بهم
نتیجه گرفته شود. برای مثال اگر دو میخ باشد، یک جای خالی و دو میخ دیگر، (
)
کدامیک از این دو عدد را نمایش میدهد باید از روی زمینه و موقعیت علائم نسبت بهم
نتیجه گرفته شود. برای مثال اگر دو میخ باشد، یک جای خالی و دو میخ دیگر، (![]()
![]() )
آنگاه دسته سمت چپی میخها نشان دهنده دو شصت تا، یا همان 120 است و دسته سمت
راستی میخها نشان دهنده عدد 2 است. بنابراین
)
آنگاه دسته سمت چپی میخها نشان دهنده دو شصت تا، یا همان 120 است و دسته سمت
راستی میخها نشان دهنده عدد 2 است. بنابراین ![]()
![]() نشان دهنده جمع این دو عدد است که میشود 122.
نشان دهنده جمع این دو عدد است که میشود 122.
این روش
میتواند به اعداد خیلی بزرگتری بسط داده شود. یک میخ میتواند بمعنای 1، یا 60 ،
یا 3600 =60×60، یا 216.000=60×60×60 و غیره باشد. در قسمت پائینی شکل، سه دسته از
حروف میخی را داریم (![]() )
که نشان دهنده 12+ 60×3 + 60×60 است که ما آنرا بصورت 3.792 مینویسیم. مشکل بزرگی
که دراینجا وجود دارد این است که این نوع عدد نویسی ابهاماتی را در بر دارد. اگر
تنها چیزی که نوشته شده دو میخ باشد آیا این به معنی 2 است؟، یا 60×2 ؟ و یا 60×60
؟ تا زمان اسکندر کبیر بابلیها با استفاده از یک جفت میخ کج شده، که نشان میداد
در شکاف داده شده هیچ عددی نمیآید، این ابهامات را برطرف کردند، درعمل آنها نوعی
علامت را برای صفر ابداع نمودند.
)
که نشان دهنده 12+ 60×3 + 60×60 است که ما آنرا بصورت 3.792 مینویسیم. مشکل بزرگی
که دراینجا وجود دارد این است که این نوع عدد نویسی ابهاماتی را در بر دارد. اگر
تنها چیزی که نوشته شده دو میخ باشد آیا این به معنی 2 است؟، یا 60×2 ؟ و یا 60×60
؟ تا زمان اسکندر کبیر بابلیها با استفاده از یک جفت میخ کج شده، که نشان میداد
در شکاف داده شده هیچ عددی نمیآید، این ابهامات را برطرف کردند، درعمل آنها نوعی
علامت را برای صفر ابداع نمودند.
چرا بابلیها
بجای دستگاه معمول اعشاری از این دستگاه شصتتایی استفاده میکردند؟ شاید آنها از
خواص مفید عدد 60 تاثیر گرفته باشند: 60 تعداد زیادی مقسومعلیه دارد. این عدد
بطور کامل بر اعداد 2، 3، 4، 5 و 6 قابل تقسیم. این عدد همچنین بر اعداد 10،
12، 15، 20 و 30 قابل قسمت است. هنگامی که صحبت بر سر تقسیم محصول، و یا
زمین میان چند نفر باشد، این مورد میتواند خصوصیت خوشآیندی بحساب آید.
نهایتاً
ممکن است خصوصیت دیگری نیز در این زمینه سرنوشت ساز بوده باشد، و آنهم روش بابلیها
برای اندازه گیری زمان است. اگرچه آنها منجمین خوبی بودند و میدیدند که یک سال
365 روز (و یا حتی دقیقتر، 365 و یک چهارم روز) است، بنظر میرسد که آنها سادهتر
میدیدند که سال را به 360 روز تقسیم کنند. جاذبه رابطه حسابی 60×6=360 برای آنها
فوقالعاده اغوا کننده بود. بویژه وقتی به زمان ارجاع میشد، بابلیها قاعدهای را
که میگفت هر بار که مکان رقمی یکی به سمت چپ میرود، مقدار آن باید در عدد شصت
ضرب شود را به حالت تعویق درآوردند و آن را با شش جایگرین کردند. بنابراین چیزی که
باید به معنای 3600 باشد را درعمل به 360 تعبیر میکردند.
امروزه هم
ما دایره را به 360 درجه تقسیم میکنیم (یک درجه برای هر روز از سال بابلی)، هر
ساعت را به 60 دقیقه و هر دقیقه را به 60 ثانیه، این تکیه بر اعداد 60 و 360
هنوز هم با ما باقی مانده. سنتهای فرهنگی قدیمی قدرت ماندگار عجیبی را دارا هستند.
من هنوز هم گاهی اوقات متعجب میشوم که چرا در عصر کامپیوتر هنوز هم برخی از
فیلمسازان، تاریخ ساختن اثر خود را برحسب اعداد رومی بیان میکنند[26].
نابو-
شَمَش تمام مطالب ذکر شده را (البته به غیر از عدد ”صفر“ که قرنها بعد ابداع شد)
در اولین مراحل آموزشی خود یادمیگرفت. او بتدریج یاد میگرفت که چگونه بطور سریعی
هزاران نشانه میخی را بر روی خاک رس بنویسد، و همینطور که دانشآموزان امروزی
بلاخره سر و کارشان به اعداد غیر صحیح و اعشاری میخورد، او نیز یاد میگرفت چگونه
با استفاده از روشهای بابلی با کسرهایی مثل یک دوم، یک سوم، و یا حتی کسور پیچیدهتری
که در رصدهای نجومی با آنها برخورد میکرد، کار کند.
بمنظور
کوتاه نویسی اعداد با خط میخی، دانشمندان امروزی از مخلوطی از شیوههای کهنه و
بعضی روشهای جدید استفاده میکنند. آنها برای نوشتن اعداد اعشاری که در گروههای
پشت سرهم ظاهر میشد از کاما برای جدا کردن آنها استفاده میکنند. در اینجا ما هم
از همین روش استفاده میکنیم.
خوب حالا
ببینیم چگونه یک کاتب بابلی عدد ”یک دوم“ را مینوشت. ما در دستگاه حسابی خودمان
این عدد را به روشهای متفاوتی مینویسیم. ما این عدد را یا بصورت ½، و یا با
استفاده از ممیز اعشاری آن را بصورت 0.5 مینویسم. حالت کسری
قابل لمستر است و از نظر تاریخی زودتر آمده؛ درک ممیز اعشاری قدری مشکلتر است
ولی از نظر محاسباتی قدرت بیشتری دارد، زیرا نوشتن آن حالتی از گسترش طبیعی و
”جایگاه-محور“ اعداد صحیح است. عدد 5 در 0.5 یعنی ”پنج تقسیم بر
ده“، و در 0.05 یعنی ”پنج تقسیم بر صد“. با حرکت هر رقم به سمت چپ، آن
عدد در 10 ضرب، و با هر حرکت به سمت راست بر 10 تقسیم میشود.
بنابراین
حساب اعشاری مانند حساب با اعداد صحیح است، با این تفاوت که شما باید حساب جایی که
ممیز اعشار قرار میگیرد را داشته باشید.
بابلیها
نیز چنین ایدهای داشتند، ولی مبنای آنها 60 بود. کسر 2/1 باید بصورت مجموعی از
کسر 60/1 بیان شود. بطور وضوح این عدد 60/30 است، و آنها ”یک دوم“ را بصورت 30؛0
مینوشتند، و در اینجا دانشمندان امروز از علامت ”؛“ برای ممیز شستگانی استفاده میکنند
(همان کاری که ممیز اعشاری در مبنای ده انجام میدهد) و همانطور که پیشتر
بیان شد اگر بخواهیم آنرا به خط میخی نمایش دهیم طولانی میشود. بابلیها با
استفاده از این روشها حقیقتاً توانستند محاسبات نسبتاً پیشرفتهای را انجام دهند:
برای مثال مقداری که برای جذر عدد 2 بدست آوردند 24،51،10؛1 بود که خطای آن نسبت
به مقدار واقعی حدود یک در صد هزار است. آنها از دقتی اینچنین، هم در ریاضیات
نظری، و هم برای نجوم، استفاده میکردند.

تا آنجا
که به مضمون اصلی ما یعنی تقارن مربوط است، مهمترین مهارتی که نابو-شمش یاد میگرفت
حل معادلات درجه دوم بود. هرچند از حدود یک میلیون لوح رُسی بجا مانده از دوران
بابل باستان تنها حدود پانصد عدد از آنها با ریاضیات سر وکار دارند، ولی ما آگاهی
نسبتاً زیادی از روشهای حل معادلات بوسیله بابلیها در دست داریم. در سال 1930 شرقشناس
معروف اُتو نُوگباِر[27] کشف کرد که یکی از این لوحها نشان دهنده
چیزیست که ما امروزه به آن معادله درجه دوم میگوئیم. معادلات درجه دوم معادلاتی
هستند که شامل یک مجهول، مربع آن مجهول و نیز یک عدد معلوم هستند. اگر مربع مجهول
در معادله نباشد، این نوع معادله، ”خطی[28]“ خوانده میشود، و حل آنها ساده است. معادلهای
که شامل مکعب یک مجهول باشد (یعنی مجهول سه بار در خودش ضرب شده باشد) ، معادلات
درجه سوم نامیده میشوند. جداول عددی پیدا شده نشان میدهد که بابلیها با استفاده
از آنها روش هوشمندانهای برای تخمین جواب برخی از معادلات درجه سوم در دست
داشتند. از نظر تاریخی تنها چیزی که موجود است و ما میتوانیم از آن مطمئن باشیم،
خود جداول است. ما تنها حدس میزنیم که چنین جداولی فقط میتوانسته برای حل معادلات
درجه سوم بکار رود. ولی لوحهایی که نُوگباِر آنها را مطالعه کرد بخوبی نشان
میدهد که کاتبین بابلی در حل معادلات درجه دوم استاد شده بودند.
یک نمونه
از آنها که قدمتش به حدود 4000 سال قبل باز میگردد میپرسد : ”طول ضلع مربعی را
بدست آورید که اگر مساحت آن مربع را منهای طول ضلع کنیم حاصل 14،30 شود“. این
مسئله شامل مربع مجهول (مساحت مربع) و خود مجهول (طول ضلع) و یک عدد معلوم (14،30)
است. به عبارت دیگر از خواننده میخواهد تا یک معادله درجه دوم را حل کند. در همان
لوح، بلافاصله راه حل و جواب مسئله داده میشود: ”نصف 1 را بگیر میشود 30؛0 .
حاصل را در خودش ضرب کن که میشود 15؛0، این عدد را با 14،30 جمع کن حاصل میشود
15؛14،30. این عدد مربع 30؛29 است. حلا 30؛0 را به 30؛29 اضافه کن، حاصل میشود 30
که طول ضلع مربع است.“
اینجا چه
گذشت؟ اجازه دهید تا مراحل طی شده را با فرم جدید دوباره باز نویسی کنیم:
1- نصف 1
را بگیر حاصل میشود 30؛0. (2/1)
2- 30؛0
را در 30؛0 ضرب کن میشود 15؛0. ( 4/1)
3- این
عدد را به 14،30 اضافه کن تا 15؛14،30 بدست آید. ( 4/1 870)
4- این
عدد مربع 30؛29 است. (2/1 29)×(2/1 29)=(4/1 870)
5- حالا
30؛0 را به 30؛29 اضافه کن. (2/1 + 2/1 29)
6- حاصل
30 است که میشود طول ضلع مربع. ( 30)
از این
میان، پیچیدهترین مرحله چهارمی است که میگوید عددی را پیدا کن که مربع آن بشود
4/1 870. عدد 2/1 29 جذر (یا ریشه دوم) عدد 4/1 870 است. جذر گرفتن ابزار
اصلی برای حل معادلات است، و هنگامیکه ریاضیدانان سعی کردند با روشهای مشابهای،
معادلات پیچیدهتری را حل کنند، جبر نوین پدید آمد.
ما بعداً
این مسئله را با استفاده از فرم امروزی معادلات درجه دوم نشان خواهیم داد. ولی مهم
است که بدانیم بابلیها از فرمولهای جبری برای حل چنین معادلاتی استفاده نمیکردند.
در عوض آنها، با ذکر یک مثال، روندی را توضیح میدادند که به جواب منتهی میشد.
ولی آنها بطور روشن میدانستند که اگر اعدادی که در مثال آمده تغییر کند
باز هم این روند جواب درست میدهد.
بطور
خلاصه آنها میدانستند که چگونه یک معادله درجه دوم را حل کنند. هرچند روش آنها از
لحاظ فرم با آنچه ما امروز بکار میبریم یکسان نیست، ولی در اساس یکی هستند.

چگونه بابلیها روش حل معادلات درجه دوم را کشف
کردند؟ هیچ مدرک موثقی در دست نیست، ولی بنظر میرسد آنها از را تفکر هندسی به این
رویکرد رسیده باشند. اجازه دهید تا مثال سادهتری را مطرح کنم که به همان روش
منتهی میشود. فرض کنید ما لوحی را یافتهایم که در آن آمده : ”طول ضلع مربعی را
پیدا کن که اگر دو برابر طولش را با مساحت آن جمع کنیم حاصل آن 24 شود. “. ما
امروزه این مسئله را به این صورت مطرح میکنیم: ”مربع مجهول بعلاوه 2 ضرب در مجهول
مساوی 24“ ما میتوانیم این مسئله را بصورت تصویر زیر نشان دهیم:
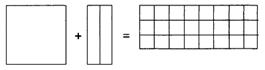
فرم تصویری یک معادله درجه دوم
در اینجا طول عمودی مربع و مستطیلی که در سمت چپ
علامت مساوی قرار گرفتهاند متناظر با مجهول هستند، و مربعهای کوچک حکم واحد را
دارند. اگر ما مستطیل باریک را به دو نیم تقسیم، و هر نیمه را به پهلو و پائین
مربع بچسبانیم، آنچه بدست خواهیم آورد یک ”مربع کامل“ است که یک گوشه (یک واحد) کم
دارد. با اضافه کردن این یک واحد به طرفین معادله ما شکل زیر را خواهیم داشت:
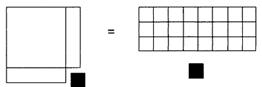
تکمیل کردن مربع
حالا ما یک مربع در سمت چپ داریم که و 25 واحد مربع
در سمت راست. و اگر آنها را بصورت 5×5 بچینیم:
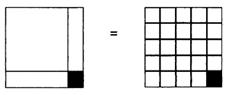
حالا حل جواب مسله واضح است
بنابراین
مربع ”مجهول منهای یک“ شده است 25. با گرفتن جذر از 25 می بینیم که ”مجهول منهای
یک“ میشود 5، و در این مرحله شما لازم نیست نابغه باشید تا نتیجه بگرید که این
مجهول برابر 4 خواهد بود.
این توصیف
هندسی دقیقاً با روشی که بابلیها برای حل معادله درجه دوم بکار میبردند مطابق
است. نمونههای بغرنجتر دیگری هم که در لوح آمده همه از همین دستورالعمل استفاده
میکنند. لوح فقط دستورالعمل را به ما میدهد ولی نمیگوید این دستورالعمل از کجا
آمده، ولی تصویر هندسی توصیف کاملیتری بدست میدهد.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
بسیاری از
بزرگترین ریاضیدانان عصر عتیق در شهر اسکندریه مصر زندگی میکردند. شهری که منشاء
آن میان پنج واحه بزرگ در غرب رود نیل، و در صحرای غربی قرار گرفته است. یکی از
این واحهها، سیوا[29] نام دارد که بواسطه دریاچههای نمک خود که
در زمستان گسترده، و در تابستان کوچک میشود، مشهور است.
مهمترین
جاذبه توریستی سیوا معبد اغورمی است که قبلاً وقف آمون[30] شده بود. آمون بقدری مقدس بود که سیمای
ظاهری او کاملاً انتزاعی بود، ولی بیشتر او را با خدای خورشید یعنی راع[31] مترادف میدانند. معبد آمون در سیوا، که در بیست و ششمین سلسله از
سلاطین مصر ساخته شده بود، خانه پیشگوهای معروفی بود که دو حادثه مهم تاریخی را
پیشگویی کردند.
اولین
آنها نابودی ارتش پادشاه ایران کمبوجیه دوم است که مصر را به تصرف خود درآورد.
گفته میشود در سال 523 ق.م کمبوجیه که میخواست بوسیله پیشگوی معبد آمون سلطنت خود
در مصر را مشروعیت ببخشد، نیرویی را بسمت صحرای غربی گسیل کرد. این ارتش به واحه
بحریه رسید ولی در راه رسیدن به سیوا با طوفان شن مواجه و نابود گشت. بسیاری از
مصرشناسان به وجود ”سربازان گمشده کمبوجیه“ شک دارند و آنرا یک افسانه میپندارند،
ولی در سال 2000، تیمی از دانشگاه حلوان که در جستجوی نفت بود، تکههایی از البسه،
فلزات و بقایای انسانی را در آن نواحی پیدا کرد، و نظر براین است که شاید اینها
بقایای سربازان گمشده باشند.
رویداد
دوم، که دو قرن بعد رخ داد، یک واقعه تاریخی است: دیدار سرنوشتساز اسکندر کبیر از
سیوا، که دقیقاً همان چیزی را جستجو میکرد که کمبوجیه به دنبال آن بود.

اسکندر[32] فرزند فیلیپ دوم، شاه مقدونی بود. کلئوپاترا، دختر فیلیپ، با شاه
اپریوس ازدواج کرد، و در هنگام جشن عروسی او بود که به فیلیپ سوء قصد شد. ممکن است
قاتل فلیپ معشوق همجنسگرای او پوسانیاس[33] بوده باشد، که بخاطر بیتوجهی او نسبت به
درخواستهایش همیشه از وی ناراحت بود، و یا ممکن است این قتل برای خنثی کردن خطر
حمله فیلیپ به ایران توسط داریوش سوم پادشاه ایران طرح ریزی شده بود. اگر چنین
باشد، نتیجه کاملاً معکوس داد، زیرا ارتش مقدونه بلافاصله اسکندر را شاه اعلام کرد
و از آن پس همانطور که معروف است، این پادشاه 20 ساله بیشتر سرزمینهای شناختهشده
آن عصر را به تصرف خود در آورد. در سال 332 ق.م در ادامه راهش بسوی کشورگشایی، او
مصر را بدون هیچ جنگی به تصرف خود درآورد.
اسکندر که
میخواست فتح خود را همچون یک فرعون استحکام بخشد، سفری به سیوا کرد تا از پیشگو
بپرسد که آیا او یک خدا هست یا نه. او به تنهایی نزد پیشگو رفت و در بازگشت، رای
او را برای همه اعلام کرد: ”آری، پیشگو تصدیق کرده که من یک خدا هستم“. این رای
باعث شد تا اقتدار وی بصورت گستردهای زیاد شود. بعدها شایعاتی پخش شد مبنی بر
اینکه پیشگو گفته که او پسر زئوس است.
معلوم
نیست که آیا مصریان با این شاهد توخالی قانع شدهاند، یا از ترس ارتش پرابهت او
چنین داستانی را قبول کردهاند. شاید آنها از حکمرانی پارسیان بستوه آمدهاند و
بدلیل اینکه اسکندر را اهریمن کوچکتری نسبت به آنها میدیدند از او با آغوش باز در
شهر ممفیس استقبال کردند. هر حقیقتی که در پشت تاریخ پنهان باشد، از آن زمان به
بعد مصریان اسکندر را بعنوان پادشاه خود محترم میشمردند.
در راه
سفر به سیوا، اسکندر که شیفته نواحی مابین دریای مدیترانه و دریاچه بحرالمريوط[34] شده بود تصمیم گرفت تا شهری را در آنجا بنا کند. شهری
که از سر احترام به او، نام اسکندریه[35] را بر آن گذاشتند. این شهر از روی طرحهای
اولیهای که خود اسکندر ارائه داد، بوسیله یک معمار یونانی بنام دونوکرات طراحی
شد. برخی تاریخ نگاران تاریخ تولد شهر را 7 آوریل 331 ق.م ذکر کردهاند و برخی نیز
آنرا نزدیک به 334 ق.م میدانند. اسکندر هیچگاه نتوانست ساخته خود را ببیند؛ تقدیر
چنین بود که ورود بعدی او به اینجا برای خاکسپاریش باشد.
بنابراین،
حداقل افتخار ساخت این شهر بنام او ثبت شد، ولی ممکن است حقیقت پیچیدهتر از این
باشد. اکنون بنظر میرسد آنچه که بعدها اسکندریه نام گرفت، قبل از ورود اسکندر نیز
وجود داشته. از خیلی وقت پیش مصرشناسان متوجه این نکته بودند که کتیبهها خیلی هم
قابل اعتماد نیستند. معروف است که معبد بزرگ کارناک بوسیله رامسس دوم بنا شده است.
ولی حقیقت این است که بیشتر ساخت آن بوسیله پدرش، سِتی، انجام شد و میتوان کتیبههای
او را در پشت کتیبههای رامسس پیدا کرد. در آن زمان چنین غصب و تصرفاتی بیسابقه
نبوده، و حتی بیاحترامی هم محسوب نمیشده.
اسکندر
دستور داد تا بر سردر تمام ساختمانهای قدیمی اسکندریه نامش را حک کنند. بعبارتی
او نام خود روی کل شهر حک کرد. اگر درگذشته فراعنه برخی از ساختمانها و یادبودهای
مهم را برای خود غصب میکردند، اسکندر تمام شهر را برای خود غصب کرد.
اسکندریه
بدل به یک بندر دریایی عمده شد، که شاخههای مختلف نیل و نیز یک آبراه منتهی به
دریای سرخ (و در نتیجه به اقیانوس هند و خاور دور)، در آن بهم پیوند میخوردند.
این شهر با داشتن کتابخانه معروف خود به مرکز دانش و یادگیری تبدیل شد. اسکندریه
محل تولد یکی از تاثیر گذارترین ریاضیدانان تاریخ نیز بود: هندسهدانی بنام
اقلیدس.

گرچه
تاثیر درازمدت اقلیدس روی تمدن بشری، بسیار بیشتر از اسکندر است، ولی اطلاعات ما
درباره او نسبت به اسکندر بسیار کمتر است. اگر نام آشنایی در ریاضیات وجود داشته
باشد، همانا ”اقلیدس“ است. هر چند ما از زندگی اقلیدس چیز زیادی نمیدانیم، ولی
آثار او خیلی خوب میشناسیم. برای چندین قرن در جهان غرب، ریاضیات و اقلیدس دو
کلمه مترادف هم بودند.
چرا
اقلیدس اینقدر معروف شد؟ ریاضیدانان بزرگتر، و چه بسا مهمتری پا به عرصه وجود
گذاشتهاند، ولی قریب به دو هزار سال نام اقلیدس برای هر دانش آموزی در اروپای
غربی، و تا حد کمتری در جهان عرب، شناخته شده بود. او مؤلف معروفترین کتاب درسی
ریاضی بود: کتاب اصول هندسه[36]، که معمولاً بصورت خلاصه اصول[37] نامیده میشود. هنگامی که چاپ اختراع شد، از اولین
کتابهایی بود که چاپ شد و تا کنون در هزار ویرایش مختلف به چاب رسیده، کتابی که
تنها انجیل میتواند از این لحاظ بر آن پیشی گیرد.
اطلاعات
ما درباره اقلیدس کمی بیش آن چیزیست که درباره هومر[38] میدانیم. او در سال 325 ق.م در اسکندریه متولد شد و
درسال 265 ق.م درگذشت.
سه نظر
درباره اقلیدس و کتاب اصول مطرح است. اول اینکه اقلیدس در زمان پیدایش کتاب اصول
زنده بوده و تنها نویسنده این کتاب است. دومی این است که او در زمان پیدایش کتاب
زنده بوده، ولی اصول را او ننوشته (حداقل بتنهایی). او ممکن است سردسته
تعدادی از ریاضیدانان دیگری بوده که بصورت مشترک کتاب اصول را پدید آوردند.
و نظریه سوم که در نوع خود جنجالیست (ولی میتواند محتمل باشد) این است که تعدادی
از ریاضیدانان مثل گروه بورباکی[39] در فرانسه بودهاند، کتاب اصول را با همکاری یکدیگر نوشتهاند و نام مستعار “اقلیدس” را بعنوان مؤلف
بر روی آن گذاشتهاند.
با این همه محتملترین داستان این است که اقلیدس وجود داشته، اقلیدس نام یک شخص
بوده و کتاب اصول را خودش جمع آوری کرده.
البته این
بدین معنا نیست که خود اقلیدس تمام ریاضیاتی را که در این کتاب آمده بتنهایی کشف
کرده. کاری که او انجام داد این بود که قسمت قابلتوجهی از ریاضیات یونان باستان را که تا آن
زمان موجود بود جمع آوری و تدوین کرد. او مطالبی را از پیشینیان خود وام گرفت و
آنرا برای آیندگان به ارث گذاشت، ولی در عین حال،
مُهر خود را بر روی آن زد.
عموماً اصول را یک کتاب هندسه توصیف میکنند، ولی در این کتاب نظریه اعداد و نوع
خاصی از جبر، (که همگی بصورت هندسی ارائه شدهاند) نیز پیدا میشود.
در مورد
زندگی خصوصی اقلیدس اطلاعات ما بسیار اندک است. برخی از نویسندگان در آثار خود
جسته گریخته اطلاعاتی را به ما میهند،
که هیچ یک از آنها مورد تائید دانشمندان امروزی نیست. آنها به ما میگویند اقلیدس در اسکندریه درس میداد، و طبیعی است که نتیجه بگیریم در همان
شهر متولد شده، ولی ما حقیقتاً از این مورد مطمئن نیستیم. هفتصد سال پس از مرگ
اقلیدس، در سال 450 ب.م فیلسوفی بنام پروکلوس[40] مینویسد:
”اقلیدس...کتاب
اصول را جمع آوری کرد، بسیاری از قضایای اودوکسوس[41] و تیآاتتوس [42] را مرتب کردو آنها را بصورت قضایای قابل
نتیجه گیری درآورد، چیزیهای که
توسط پیشینیان او فقط بصورت سطحی اثبات شده بودند. این مرد در زمان بطلمیوس اول
زندگی میکرده،
زیرا از ارشمیدس نقل شده که روزی بطلمیوس از اقلیدس پرسیده ’آیا راه سادهتری برای یادگیری هندسه وجود دارد؟ ‘ و او
درجواب گفته ’شاهان را راهی بسوی هندسه نیست‘. بنابراین او جوانتر از حلقه
افلاطونیان، ولی مسنتر از اراتوستن و ارشمیدس بوده. او اصالتاً یک کمالگرای
افلاطونی بود، زیرا او کل کتاب اصول را بر مبنای اشکال افلاطونی بنا کرد.“
روش او در
نوشتن برخی از موضوعات کتاب اصول، گواهی غیر مستقیم، اما قانع کنندهای، بر این مدعی است که او در دورهای شاگرد اکادمی افلاطون در آتن بوده است.
برای مثال فقط در آنجا بوده که او میتوانسته هندسه اودوکسوس و تیآاتتوس را یاد بگیرد.
تا آنجا
که به شخصیت او مربوط است، تنها چیزی که میدانیم از نقلقولهایی است که از پاپوس برجای مانده و او را شخصیتی
توصیف میکند ”بسیار خوشبرخورد
و پذیرای همه کسانی که قادر بودند به هر طریقی ریاضیات را توسعه دهند. همیشه مواظب
بود تا موجب رنجش کسی نشود و هر چند دانشمندی کامل بود، هیچ وقت خودستایی نمیکرد.“ حکایات اندکی از او باقی مانده، مثل این یکی که از استوبائوس نقل
شده: روزی یکی از شاگردان اقلیدس از او پرسید که اگر هندسه یاد بگیرد چه سودی
برایش دارد. اقلیدس غلامش را فراخوند و گفت ”یک سکه به این مرد بده، زیرا او برای
هر چیزی که یاد میگیرد
باید چیزی نصیبش شود.“

رویکرد
یونانیان به ریاضیات، با رویکردی که بابلیان و یا مصریان داشتند بسیار متفاوت بود.
این فرهنگها سود ریاضیات را از کاربرد عملی آن میدیدند. ولی از نظر برخی از ریاضیدانان
یونانی، اعداد نه فقط ابزاری برای تائید اعتقادات عرفانی بودند، بلکه هسته اصلی
چنین اعتقاداتی را هم تشکیل میداند.
ارسطو و افلاطون از فرقهای یاد میکنند که حول و
حوش 550 ق.م بر گرد فيثاغورث تشکیل شده بود و ریاضیات، و بویژه اعداد، را اساس کل
آفرینش میدانستند. آنها نظریاتی عرفانی درباره توازن جهان توسعه دادند که قسمتی
از آن برپایه این بنا شده بود که ”نوتهای موسیقی هماهنگ“ بر طبق یک الگوی ساده
ریاضی عمل میکنند. اگر یک تار موسیقی نوت خاصی را تولید کند، تاری که نصف طول
اولیه را داشته باشد صدایی با یک اکتاو بالاتر تولید میکند. آنها بررسیهای
گوناگونی را بر روی الگوی اعداد انجام دادند، بالاخص اعداد چندضلعی، که بوسیله
مرتب کردن اشیاء بصورت الگوهای چند ضلعی تولید میشود. برای مثال ”اعداد مثلثی“ 1،
3، 6 و 10 از روی الگوی مثلثها، و ”اعداد مربعی“ 1، 4، 9 و 16 از روی الگوی مربعها
شکل میگیرند:
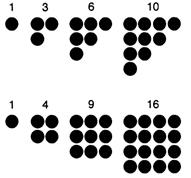
اعداد مثلثی و مربعی
مکتب
فيثاغورثي دربردارند برخی از جنبههای مضحک در مورد اعداد بود، برای مثال 2 را
نَر، و 3 را ماده میانگاشت. ولی این نظر که ساختار پایهای جهان از نوع ریاضی
است، هنوز هم در بسیاری از علوم نظری امروز مورد قبول است. هرچند که بعدها هندسه
یونانی از حالت عرفانی خارج شد، ولی یونانیان ریاضیات را بعنوان رشتهای از فلسفه
میدیدند تا یک ابزار صرف.
دلایلی
هست که به ما میگوید این کل داستان نیست. این یک حقیقت کاملاً اثبات شده است که
ارشمیدس، که خود ممکن است یکی از شاگردان اقلیدس بوده باشد، از دانش ریاضیاش برای
طراحی ماشینهای قدرتمند و ادوات جنگی استفاده میکرده. تعداد معدودی از
ماشینهای ظریف یونانی پیدا شدهاند، که طراحی ماهرانه و دقت آنها از یک سنت
کاملاً توسعه یافنه صنعتی، و به نوعی از یک نسخه باستانی ”ریاضیات کاربردی“ حکایت
میکند. شاید بهترین نمونه از این نوع را بتوان در ماشینی با چرخ دندههای بسیار
پیچیده دانست که در دریا و در نزدیکی جزایر آنتیکایترا[43] پیدا شد و ظاهراً برای کارهای نجومی و
محاسباتی از آن استفاده میشده.
کتاب اصول
اقلیدس مطمئناً در چهارچوب ریاضیات یونانی میگنجد، شاید بخاطر اینکه خود ریاضیات
یونانی عمدتاً بر پایه کتاب اصول است. تکیه اصلی کتاب بر روی اثبات منطقی است و
هیچگونه اشارهای به کاربردهای عملی نمیشود. مهمترین جنبه از کتاب اصول که به
داستان ما مربوط است، مطالبی نیست که در آن کتاب آمده بلکه موضوعاتی است که در آن
نیامده.

اقلیدس دو
کشف مهم انجام داد. اولی مفهوم اثبات (یا برهان) است. اقلیدس از قبول هر گونه
گزاره ریاضی خود داری میکرد مگر آنکه گزاره مربوطه از روی یک رشته از مراحل
منطقی، که صحت آنها از قبل معلوم است، نتیجهگیری شود. کشف دوم این را میگوید
که روند اثبات باید از جایی آغاز شود، و اینکه صحت این گزارههای اولیه نمیتواند
اثبات شود. بنابراین اقلیدس پنج اصل اولیه را قطعی فرض کرد، و بقیه استنجات او
برپایه اینها قرار میگرفت. چهارتای این اصول صریح و سادهاند: 1- از دو نقطه فقط
یک خط میگذرد؛ 2- هر پاره خط را میتوان امتداد داد؛ 3- میتوان یک دایره با هر
مرکز و هر شعاعی رسم کرد؛ 4- کلیه مثلثهای قائمالزاویه با هم مشابهاند.
ولی اصل
پنجم با کلیه موارد متفاوت بود. این اصل نسبت به موراد قبلی، کمی طولانیتر و
پیچیدهتر بود. چیزی که این اصل بیان میکرد خیلی واضح و روشن نبود. معنی ضمنی این
اصل در وجود خطوط موازی بود (یعنی خطولی که هر چقدر هم که امتداد داده شوند یکدیگر
را قطع نمیکنند). آنچه حقیقتاً اقلیدس اظهار میکرد این بود که اگر دو خط مفروض،
خط سومی را قطع کنند، دو خط اول در همان سمتی یکدیگر را قطع میکنند که مجموع
زوایای ایجاد شده آن با خط سوم کمتر از 180 درجه باشد. بعداً معلوم شد که این اصل
از نظر منطقی معادل این است که بگوئیم ”تنها یک خط وجود دارد که با خط دیگری موازی
است و از یک نقطه مفروض عبور میکند.“
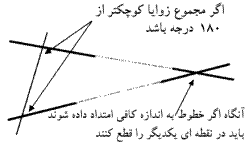
اصل پنجم اقلیدس
برای
قرنها اصل پنجم نوعی نقص تلقی میشد، چیزی که باید آنرا از “اصل بودن” خارج کرد و
صحتش را از روی چهارتای دیگر نتیجه گرفت، و یا حداقل آن را با چیز سادهتر و
روشنتری جایگزین کرد. این بدبینی تا قرن نوزدهم ادامه داشت و در این زمان بود که
ریاضیدانان فهمیدند که اقلیدس کاملاً مُحق بوده که این را بعنوان یک اصل مطرح
کرده، زیرا صحت آنرا نمیتوان از اصول دیگر استنتاج کرد.

از نظر
اقلیدس، اثبات منطقی یک وجه اساسی هندسه بود، و هنوز هم ”اثبات و برهان“ بعنوان یک
رکن اساسی در تشکیلات ریاضی باقی مانده. در گزارهای که فاقد برهان است باید تردید کرد، حال
هرچقدر هم که مدارکی برای تائید آن وجود داشته باشد، باز هم مهم نیست. فیزیکدانان،
مهندسان و منجمین معمولاً از اثبات بیزارند، و آنرا بعنوان چیزی زائد و فضلفروشانه تلقی میکنند. دلیلش هم این است که آنها روش موثرتری
برای صحت گفتههای
خود دارند، و آنهم چیزی نیست جز آزمایش و مشاهده.
برای
مثال، تصور کنید که یک منجم سعی دارد حرکت ماه را محاسبه کند. او برای محاسبه حرکت
ماه از معادلات ریاضی استفاده میکند،
ولی همانجا گیر میافتد،
زیرا هیچ راهی بنظرش نمیرسد که
بتوان این معادلات را بطور کامل و دقیق حل کرد. بنابراین ممکن است منجم معادلات
اصلی را دستکاری کند تا به تقریبهای
سادهتری دست پیدا کند. این
نوع تقریب زدنها
باعث نگرانی یک ریاضیدان میشود،
زیرا او فکر میکند این تقریبها
ممکن است تاثیرات جدی روی جواب مسئله داشته باشد، و بنابراین چون میخواهد از بیخطر بودن آنها مطمئن شود به
برهان و اثبات روی میآورد.
منجم روش دیگری برای بررسی صحت و سقم کارهای خود دارد. او میتواند مشاهده کند که
آیا حرکت ماه با محاسبات او همخوانی دارد یا نه. اگر همخوانی داشت، آنگاه همزمان
این هم موجب توجیه روش او میشود
(زیرا جواب درست را بدست آورده) و هم صحت نظریه را تائید کرده (به همان دلیل
قبلی). این منطق یک دور باطل نیست زیرا اگر این روش از نظر ریاضی نامعتبر باشد،
آنگاه هرگز نمیتواند حرکت ماه را پیشبینی کند.
ریاضیدانان،
که از نعمت مشاهده و یا آزمایش بیبهرهاند، مجبورند کارهای خود را با منطق درونی
آن محک بزنند. هر چقدر معنی گزاره مهمتر
باشد، آنگاه اثبات صحت آن مهمتر و واجبتر میشود. بنابراین هنگامی که گزاره مورد نظر
چیزی باشد که همه میخواهند صحیح باشد، و یا اگر صحیح باشد مستلزم موارد مهمی است،
آنگاه اثبات آن از قبل هم واجبتر میشود.
اثبات و برهان نمیتواند بر اصولی نامشخص بنا شود، و نمیتواند بصورت نامتناهی به اصول دیگر
تکیه کند. برهان باید از جایی شروع شود، و برحسب تعریف، این نقطه شروع چیزهایی هستند که نه اثبات شده هستند
(و نه بعداً اثبات میشود).
امروزه ما به این چیزهای فرضی اثبات نشده “اصول موضوعه” یا اکسیوم[44]، میگوییم.
اصول موضوعه در ریاضیات حکم قاعده بازی را دارند.
هرکسی که
به اصول موضوعه اعتراض داشته باشد، اگر بخواهد میتواند آنها را تغییر دهد، ولی حاصل اینکار
بازی دیگری خواهد بود. ریاضیات مدعی نیست که برخی گزارهها حتماً صحیح
هستند. بلکه میگوید
اگر ما اصول موضوعه مختلفی را قبول کردیم، آنگاه گزارههایی که از آنها برمیآید،
باید برآیند منطقی آنها باشد. این مورد دال بر این نیست که اصول موضوعه قابل تغییر
نیستند. ریاضیدانان ممکن است بر سر اینکه کدامیک از دستگاههای اصل موضوعی (یا اکسیوماتیک) برای یک
منظور بخصوص بهتر هستند، و یا از نظر ذاتی دارای ویژگی و جذبه خاصی هستند، با هم
بحث کنند. ولی این بحثها
درباره منطق درونی هیچ یک از این دستگاههای اکسیوماتیک (یا بازیها) نیست، بلکه در مورد این است که کدامیک
از آنها ارزش بازیکردن
را دارد، یا کدامیک جالبتر، ویا خوشآیندتر
است.

نتیجه
اصول موضوعه اقلیدس، یا همان سلسلهای از
نتیجهگیریهای منطقیِ طولانی و
بادقت انتخاب شده، تاثیرات بسیار فراگیری داشته است. برای مثال او با منطقی که در
زمان خودش بسیار بینقض مینمود، ثابت کرد که اگر شما اصول موضوعه او
را قبول کردید آنگاه میتوانید موارد زیر را بصورت ضمنی از آنها نتیجه بگیرید:
·
مربع وتر یک مثلث قائمالزاویه برابر مجموع مربعات دو ضلع دیگر
است.
·
تعداد بینهایتی از اعداد اول وجود دارند.
·
اعداد غیرگویا (گنگ) وجود
دارند که قابل نمایش بصورت کسر نیستند. یک نمونه از آنها جذر عدد 2 است.
·
تعداد چندوجهیهای منظم دقیقاً
5 عدد است: چهار-وجهی، مکعب، هشت-وجهی، دوازده-وجهی و بیست-وجهی.
·
اگر فقط خط کش و پرگار در دست
باشد، میتوان
با استفاده از آنها هر زاویهای را
دقیقاً به دو قسمت مساوی تقسیم کرد (ولی مثلاً نمیشود فقط با استفاده از خطکش و
پرگار زاویه را به سه قسمت مساوی تقسیم کرد).
·
اگر فقط خط کش و پرگار در دست
باشد، میتوان
با استفاده از آنها 3، 4، 5، 6، 8، 10 و 12 وجهی رسم کرد (ولی نمیشود با خطکش و
پرگار بتنهایی مثلاً 7 وجهی رسم).
من از
اینها بعنوان “قضایای” ریاضی نام میبرم.
در زبان امروزه هر گزاره ریاضی که اثباتی برای آن وجود دارد یک ”قضیه“ نامیده میشود. ولی نقطه نظر اقلیدس کمی فرق داشت: او
صریحاً با اعداد کار نمیکرد.
دید او بیشتر هندسی بود. مثلاً هرچیزی که ما آن را عدد تلقی میکنیم، او از آنها تحت عناوینی از قبیل طول،
مساحت، و حجم یاد میکرد.

محتوای اصوا
اقلیدس به دو مقوله عمده تقسیم میشود. یکی قضایا[45] هستند که از درستی چیزی به شما میگویند. و
دیگری راهکارها[46] هستند که چگونگی انجام چیزی را بشما
میگویند.
یک نمونه معروف از قضایا، گزاره شماره 47 جلد اول
اصول است، که معمولاً بعنوان قضیه فیثاغورث شناخته میشود. این قضیه به ما میگوید
که رابطه ویژهای بین بزرگترین ضلع یک مثلث قائمالزاویه، و دو ضلع دیگر وجود
دارد.
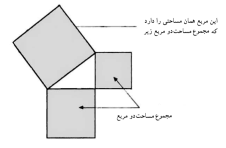
قضیه فیثاغورث
یک نمونه از راهکار که در داستان ما اهمیت دارد
گزاره شماره 9 از جلد اول است، جایی که اقلیدس مسئله تنصیف (یا نصف کردن) زوایا را
حل میکند.
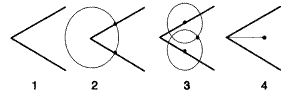
چگونگی تنصیف (نصف کردن) یک زاویه با
استفاده از خط کش و پرگار
باتوجه به
محدود بودن فنون قابل دسترس در دوران اولیه توسعه ریاضیات، روش تنصیف زاویه ساده،
ولی ماهرانه است. (1) زاویهای مابین دو پاره خط داده شده است، (2) پرگار را در
نقطه تلاقی این دو پارهخط قرار دهید و دایرهای رسم کنید که این دو پاره خط را در
دو نقطه قطع کند (نقاط تیره در شکل بالا). (3) حالا دو دایره با شعاع یکسان رسم
کنید که مرکز آنها این دو نقطه باشد. این دو دایره، در دو نقطه یکدیگر را قطع میکنند
(که فقط یکی از آنها بصورت تیره نشان داده شده). و بلاخره (4) این نقطه را با
استفاده از یک خط کش به نقطه تقاطع دو پاره خط وصل کنید. با این کار دو زاویه
مساوی خواهیم داشت.
با تکرار
این ”راهکار“ شما میتوانید یک زاویه را به چهار، هشت و یا شانزده قسمت مساوی
تقسیم کنیم. همینطور که معلوم است اعداد در هر مرحله دو برابر میشوند، و
بنابر این ما توانهای مختلف عدد 2 یعنی 2، 4، 8، 16، 32، 64 و ... را خواهیم داشت.

همانگونه
که قبلاً اشاره کردم مهمترین وجه کتاب اصول که به داستان ما مربوط است، آن چیزی
نیست که این کتاب در بردارد، بلکه آنی است که در این کتاب نیست. اقلیدس هیچ راه
حلی برای مسائل زیر فراهم نمیکند:
·
راهکاری برای تقسیم یک زاویه
به سه قسمت مساوی، فقط با استفاده از ”خط کش و پرگار“ (مسئله تثلیث زاویه).
·
راهکاری برای ساختن یک 7-ضلعی
منظم.
·
راهکاری برای ساختن یک پاره
خط که طول آن با مساحت یک دایره مفروض مساوی باشد (مسئله راستکردن دایره).
·
راهکاری برای ساختن یک مربع
که مساحت آن با مساحت یک دایره مفروض مساوی باشد. (مسئله تربیع دایره).
·
راهکاری برای ساختن یک مکعب
که حجم آن دقیقاً دو برابر یک مکعب مفروض باشد. (مسئله تضعیف مکعب).
برخی
اوقات گفته شد که خود یونانیها این کمبودها را نقیصهای در کار بیاد ماندنی
اقلیدس میدیدند و تلاشهای زیادی در برطرف نمون آن انجام دادند. مورخین ریاضی
شواهد کمی برای تصدیق چنین مدعای بدست میدهند. در حقیقت یونانیان بشرطی میتوانستد
این مسائل را حل کنند که از روشهایی استفاده میکردند که در چهارچوب ریاضیات
اقلیدسی نمیگنجید. کلیه راهکارهای اقلیدس با یک خط کش غیر مدرج و یک پرگار انجام
میشد. هندسهدانان یونان اگر از منحنیهای خاصی بنام مقاطع مخروطی استفاده میکردند
میتوانستند زاویه را به سه قسمت تقسیم کنند؛ آنها اگر از منحنی خاصی بنام
قوس تربیع[47] استفاده میکردند میتوانستند دایره را تربیع کنند. از سوی دیگر،
بنظر نمیرسد که آنها از این موضوع اطلاعی داشتند که ”اگر بتوان زاویه را به سه
قسمت مساوی کرد آنگاه میتوان با استفاده از آن یک 7-ضلعی منظم ساخت“. البته منظور
من دقیقاً 7-ضلعی است، روش آسانی برای 9-ضلعی وجود دارد ولی روش ساخت 7-ضلعی بسیار
ماهرانه است. در حقیقت، ظاهراً آنها به هیچ وجه توجهی به پیآمدهای مسئله تثلیث
زاویه نداشتهاند.
بعدها ریاضیدانان کمبودهای اقلیدس را از جنبههای
کاملاً متفاوتی مورد توجه قرار دادند. آنها بجای اینکه در جستجوی ابزارهای جدیدی
برای حل مسائل ذکر شده باشند، درجستجوی این بودند که با ابزارهای محدودی که اقلیدس
بکار میبرد (یعنی خط کش غیر-مدرج و پرگار) چه کارهایی میتوان انجام داد. و البته
هیچ تقلبی هم نباید درکار باشد، چون یونانیان میدانستند با خط کش مدرج
میتوان زاویه را به سه قسمت تقسیم کرد. چنین روشی بوسیله ارشمیدس ابداع شد.
یافتن آنچه میتواند، و آنچه نمیتواند در این قالب انجام شود، و سعی در
اثبات آن، وقت زیادی از ریاضیدانان گرفت. بلاخره، تا اواخر سالهای 1800 طول کشید
تا ما متوجه شویم که هیچ یک از مسائل فوق را نمیتوان بتنهایی با خطکش غیر-مدرج و
پرگار به انجام رساند.
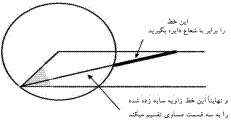
روش ارشمیدس برای تثلیث زاویه
این رخداد
قابل توجهای بود. ریاضیدانان بجای اینکه ثابت کنند یک روش خاص میتواند یک مسئله
خاص را حل کند، یادگرفتند تا مخالف آنرا ثابت کنند، آنهم در قویترین وجه ممکن:
یعنی ثابت کردند که هیچ روشی، حال از هر نوع که باشد، قادر به حل این یا آن
مسئله نیست. کمکم ریاضیدانان به محدودیت ذاتی موضوعات خود پی بردند و در همان حال
که با آب و تاب مجذوب کنندهای این محدودیتها را شرح میدادند، توانستند ثابت
کنند که اینها حقیقتاً محدودیت هستند.

به امید
اینکه هیچ تصور غلطی پیش نیاید، مایلم چند جنبه مهم از مسئله تثلیث را گوشزد کنم.
چیزی که
در اینجا مراد مسئله است یک راهکار دقیق و کامل است. در قالببندی
ایدآل یونانی از هندسه، جایی که خطوط بصورت بینهایتی باریکاند و اندازه نقاط صفر
است، این شرط ”دقیق و کامل بودن“ بصورت بسیار صریحی درصورت مسئله ذکر شده.
مسئله میگوید تقسیم زاویه به سه قسمت کاملاً مساوی. نه اینکه مثلاً با
تقریب یک در میلیون یا یک در صد-بیلیون. آنچه ساخته میشود باید بصورت بینهایتی
دقیق باشد؛ به همین نحو ما نیز میتوانیم با دقت بینهایتی سوزن پرگار خود را روی هر
نقطهای که به ما داده شده، یا بعداً حاصل میشود، قرار دهیم؛ ما میتوانیم دهانه
پرگار را با دقت بینهایتی باز کنیم، تا با فاصله دو نقطهای که به ما داده میشود
برابر باشد؛ و نهایتاً ما میتوانیم با خطکش خود خطوطی را رسم کنیم که دقیقاً
از چنین نقاطی عبور کند.
این ”دقت
و کمال“ چیزی نیست که در دنیای آشفته واقعی روی دهد. پس آیا هندسه اقلیدس در دنیای
واقعی بیفایده است؟ نه اینطور نیست. برای نمونه اگر شما با استفاده از یک پرگار
واقعی، و بر روی یک کاغذ واقعی، آنچه را که اقلیدس در گزاره شماره 9 کتاب اصول
تجویز کرده انجام دهید، آنگاه خواهید دید که زاویه به شکل نسبتاً خوبی به دو قسمت
تقسیم میشود. این روشی بود که تا قبل از ظهور گرافیک کامپیوتری طراحان و نقشهکشها
از آن برای نصف کردن زوایا، در رسم نقشههای فنی از آن استفاده میکردند. ایدآلسازی
یک نقص نیست، اصلاً دلیل عمده کارکرد ریاضیات همین ایدآلسازی است. در یک مُدل
ایدآل این امکان وجود دارد که بصورت منطقی استدلال کرد. زیرا ما میدانیم که اشیاء
مورد نظرمان چه خواصی را دارا هستند. این شباهتی به دنیای درهم و برهم واقعی
ندارد.
ولی ایدآلسازی
محدودیتهایی نیز دارد که مدل را نامناسب میکند. برای مثال خطکشیهای وسط خیابان
را نمیتوان همچون خطوط بینهایت باریک درنظر گرفت. مدل باید بر اساس زمینه کار
بصورت مناسبی تنظیم شود. مدل اقلیدس طوری تنظیم شده بود که به ما کمک میکرد تا
بستگی منطقی بین گزارههای هندسی را نتیجه بگیریم. ایدآل سازی، حتی بعنوان پاداش
هم که شده، ممکن است به ما کمک کند تا جهان واقعی را بهتر درک کنیم، ولی مطمئناً
چنین چیزی در افکار اقلیدس حکم محوری نداشته.
تعبیر
بعدی، هرچند به بحث ما مرتبط است ولی به جنبههای دیگری نظر دارد. مشکل در پیدا
کردن یک روش تقریبی برای تثلیث زاویه نیست. چه شما بخواهید اینکار را با تقریب یک
درصد انجام دهید و یا یک هزارم درصد، تفاوتی نمیکند و اینکار شدنی است (تاکید میکنم
بصورت تقریبی). برای رسم نقشههای فنی مشکلی نخواهد بود که خطای کار، یک هزارم
ضخامت خطی باشد که مداد شما رسم میکند. از نظر ریاضی مسئله درباره تثلیث ایدآل
زاویه است. آیا میتوان فقط با استفاده از خطکش غیر مدرج و پرگار یک زاویه مفروض
را دقیقاً به سه قسم تقسیم کرد؟ و جواب این مسئله ریاضی ”نه“ است.
اغلب گفته
میشود که ”شما نمیتوانید نفی وجود چیزی را ثابت کنید“. ریاضیدانان میدانند که
چنین حرفهایی پوچ است. علاوه بر این ”نفیها“ جاذبههای خاص خودشان را دارند، علیالخصوص
وقتی به روشهای جدیدی برای اثبات آنها نیاز باشد. این روشها اغلب قدرتمندتر و
جالبتر از روشهای ”اثبات وجود“ هستند. وقتی کسی روش جدیدی را ابداع کند که با آن
بتوان مشخص کرد که چه چیزهایی را میتوان با خطکش و پرگار درست کرد، و آنها را از
چیزهایی که نمیتوان درست کرد تمیزداد، آنگاه شما یک روش کاملاً جدید فکری دارید،
که بدنبال آن اندیشههای جدید، مسائل جدید، راهحلهای جدید و نظریات و ابزارهای
جدید ریاضی خواهد آمد.
هیچ کس
نمیتواند از ابزاری که هنوز ساخته نشده استفاده کند. اگر تلفن موبایلی وجود
نداشته باشد، شما نمیتوانید با موبایل به دوستتان زنگ بزنید. شما نمیتوانید
خوراک سوفله اسفناج بخورید اگر هنوز کشاورزی و یا آتش اختراع نشده باشند. بنابراین
ابزار-سازی به همان اندازه اهمیت دارد که مسئله-حلکردن.

قابلیت
تقسیم زوایا به قسمتهای مساوی، بطور نزدیکی با مسئله زیباتری رابطه دارد: ساختن
چندضلعیهای منظم.
چندضلعی یک شکل بسته است که از بهم وصل کردن خطوط
راست بدست میآید. مثلثها، مربعها، مستطیلها و لوزیهایی شبیه این همه چندضلعی
هستند. دایره یک چندضلعی نیست، زیرا ”ضلع“ آن یک منحنی است، و نه یک سری خطوط
راست. یک چندضلعی درصورتی منظم است که طول تمام اضلاع آن باهم مساوی و زاویایی هم
که هر دو ضلع مجاور با یکدیگر میسازند با هم برابر باشند. در شکل زیر چندضلعیهای
با تعداد اضلاع 3، 4، 5، 6، 7 و 8 مشاهده میکنید:

چند ضلعیهای منظم
نام
آنها بترتیب از چب به راست عبارت است از: مثلث متساویالاضلاع، مربع، پنجضلعی، ششضلعی،
هفتضلعی و هشتضلعی. این نامگذاری ممکن است مسخره باشد ولی وقتی میخواهیم به یک
چندضلعی که تعداد اضلاع آن معلوم نیست و اسمی هم برای آن موجود نیست رجوع کنیم
کافیست تعداد اضلاع را پیش از کلمه ”ضلعی“ بیاوریم و مثلاً بگویئم 17-ضلعی.
اقلیدس و
اسلاف او، باید به این مسئله که از میان چندضلعیهای منظم کدام را میتوان با خطکش
و پرگار ساخت زیاد فکر کرده باشند، زیرا برای ساخت بسیاری از آنها راهکار دادهاند.
معلوم شده که این مسئلهای جالب، و بطور قطع دشوار است. یونانیان باستان میدانستند
که اگر تعداد اضلاع یک چندضلعی یکی از اعداد زیر باشد چگونه آنرا بسازند:
3,
4, 5, 6, 8, 10, 12, 15, 16, 20
اکنون ما
میدانیم که اگر تعداد اضلاع یکی از اعداد زیر باشد نمیتوان با استفاده از خطکش
و پرگار چندضلعی را ساخت:
7, 9, 11,
13, 14, 18 ,19
از میان
این دو لیست تنها عددی که در هیچ یک قرار ندارد عدد 17 است. داستان ساخت 17-ضلعی
را بعداً و به موقع خودش توضیح خواهیم داد. این موضوع صرفاً از نظر ریاضی اهمیت
دارد.
در مباحث هندسی هیچ چیزی جای ترسیم روی کاغذ، و
استفاده از یک خطکش و پرگار واقعی را نمیگیرد. اینکار حسی را به شما میبخشد که
چگونه موضوع مورد نظر با آنچه میکشید تطبیق داده میشود. در اینجا میخواهم روش
محبوب خودم را برای ساخت شش ضلعی منظم برای شما توضیح دهم. من این را از کتابی به
نام ”انسان باید اندازه بگیرد“، یاد گرفتم که عمویم در اواخر سالهای دهه 1950 به
من داد، و واقعاً دوست داشتنی بود.
روش ساخت یک شش ضلعی منظم با استفاده از
پرگار و خط کش
دهانه
پرگار را ثابت نگاه دارید تا کلیه دایرههای رسم شده، اندازه یکسانی داشته باشند.
(1) یک دایره رسم کنید. (2) نقطهای را روی این دایره انتخاب کنید و به مرکز آن
دایرهای دیگری رسم کنید. این دایره، دایره اولیه را در دو نقطه قطع میکند. (3)
به مرکزیت هر کدام از این دو نقطه دو دایره دیگر رسم کنید تا دو نقطه دیگر حاصل
شود که دایره اولیه را قطع کنند. (4) به مرکزیت هر کدام از این نقاط دوایری رسم
کنید. حالا میتوان شش نقطه حاصله را با کمک خط کش به هم وصل کرد تا یک شش ضلعی
منظم شکل بگیرد. از نظر زیباشناسی (ولی نه لزوماً ریاضی) خوشآیندتر است که شکل را
با (5) رسم یک دایره دیگر به مرکز نقطه ششم کامل کرد. این شش دایره در مرکز دایره
اصلی همدیگر را قطع میکنند، و یک شکل شبیه گل بوجود میآورند.
اقلیدس از
روشی مشابه این استفاده میکرد، که گرچه به زیبایی روش بالا نبود ولی سادهتر بود،
و او ثابت کرد که روش او جواب میدهد. شما میتوانید آنرا در گزاره 15 از
جلد چهارم پیدا کنید.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
خورشید
کمند صبح بر بام
افکند کیخسرو
روز باده در جام افکند
می خور که
منادی سحرگه
خیزان
آواز «اشربو» در ایام افکند
در نظر
بسیاری از ما، نام عمر خیام با اشعار کنایهآمیزش بنام رباعیات، و مخصوصاً
ترجمه زیبای آن به زبان انگلیسی توسط ادوارد فیتزجرالد[48]، گره خورده. اما از نظر مورخین ریاضی، شهرت
خیام بیش از اینهاست. او در میان ایرانیان و اعراب ریاضیدان برجستهای بود. وی
مشعلی را که یونانیان رها کرده بودند بلند کرد و در حالیکه دانشمندان در اروپای
غربی به دورانی تاریک نزول کرده، و بدلیل مشاجرات مذهبی از قضایا و برهان دست
کشیده بودند، شروع به بسط نوع جدیدی از ریاضیات کرد.
از میان
دستآوردهای بزرگ خیام حل معادلات درجه سوم به کمک روشهای یونانی است. البته
روشهای او الزاماً از کاربرد خطکش و پرگار، که محدود کننده هندسه اقلیدسی، بود
فراتر میرفت، زیرا حقیقتاً این ابزارها برای اینکار ساخته نشده بودند. این حقیقتی
بود که یونانیان هم به آن ظن داشتند ولی نمیتوانستند آنرا ثابت کنند، و دلیلش هم
این بود که آنها فاقد نقطه نظر لازم بودند، که البته آن فقدان هم مربوط به هندسه
نبود، بلکه به جبر ربط داشت. ولی روشهای خیام نیز، خیلی از خطکش و پرگار
فراتر نرفت. او برای کار خود به منحنیهای خاصی بنام ”مقاطع مخروطی[49]“ تکیه کرد. بدلیل اینکه میتوان آنها را بوسیله قطع کردن یک
مخروط با یک صفحه بدست آورد، آنها مقاطع مخروطی نام گرفتند.

درمیان
نویسندگان کتابهای عامهفهمِ علمی یک باور عمومی وجود دارد که با آوردن هر معادله
در کتاب، فروش آن به نصف تقلیل پیدا میکند. اگر چنین چیزی درست باشد، خبر بدی
است، زیرا هیچکس قادر نیست تا موضوع اصلی این کتاب را بدون نشان دادن آنها در قالب
چند معادله درک کند. برای نمونه، فصل بعدی کتاب درباره کشف فرمول حل عمومی معادلات
درجه سوم و چهارم در دوران رنسانس است. من میتوانم از نمایش فرمول حل معادلات
درجه چهارم صرف نظر کنم، ولی برای ادامه کارمان ما حقیقتاً نیاز خواهیم داشت تا به
فرمول معادله درجه سوم نگاهی بیاندازیم. درغیر این صورت اگر بخواهم فقط از توضیح
لفظی استفاده کنم، آن توضیح بسیار طولانی و از خود فرمول پیچیدهتر خواهد بود.
برخی از
نویسندگان این باور عمومی را به چالش کشده و حتی در مورد معادلات هم کتاب
نوشتهاند. حالا هم چنین برمیآید که کتاب حاضر درمورد معادلات است. ولی همانگونه
که شما میتوانید در مورد کوهستان کتاب بنویسید، و خوانندگان شما هم نیازی به از
کوه بالا رفتن نداشته باشند، همینطور هم میتوانید در مورد معادلات کتاب بنویسید و
خوانندگانتان هم لازم نیست تا معادلهای را حل کنند. ولی هنوز هم این مورد صدق میکند
که خوانندگانی که اصلاً کوهستان را ندیدهاند، نخواهند توانست کتاب مربوط به آن را
درک کنند. بنابراین اگر من هم بتوانم چند نمونه از معادلاتی را که با دقت برگذیدهام
به شما نشان دهم، حقیقتاً کمک بزرگی برای هر دو ما خواهد بود.
من فقط میخواهم
شما معادلات را ببینید. لازم نسیت که با آنها کاری بکنید. من هنگامی که
لازم شد معادلات را جزء به جزء برای شما تشریح میکنم و خواهم گفت که کدام وجه از
آنها به داستان ما ربط دارد. من هرگز از شما نخواهم خواست تا معادلهای را حل کنید، و یا روی آن محاسبهای انجام دهید. و بطور کلی تا آنجا که امکان
دارد از آنها پرهیز خواهم کرد.
هنگامی که
با معادلات آشنا میشوید
آنها حقیقتاً دوست داشتنی خواهند بود. معادلات، روشن، کوتاه، و حتی در برخی موارد
زیبا هستند. حقیقت پنهانی که در مورد معادلات وجود دارد این است که آنها زبان ساده
و روشنی هستند برای توصیف ”دستوالعملهای“ محاسبه. اگر من بتوانم این دستوالعملها را بصورت لفظی برای شما بیان کنم، یا
اینکه این حس را به شما منتقل کنم که چه اتفاقی درحال افتادن است، اینکار را بدون استفاده از
معادلات خواهم کرد. گرچه در برخی موارد استفاده از الفاظ چنان دشوار خواهد بود که
من بناچار از علائم و فرمولها
استفاده میکنم.
سه علامت
مهم در این کتاب حائز اهمیت هستند که من دوتای آنرا حالا توضیح میدهم. یکی از
آنها رفیق دیرین ما، یعنی x
”مجهول“ است. این علامت نشان دهنده عددی است که ما هنوز مقدار آنرا نمیدانیم، ولی
بدنبال یافتن آن هستیم.
نوع دیگری
از علامتها،
اعداد کوچکی شبیه به 2 ، 3 و یا 4 هستند که
بصورت بالانویس نوشته میشوند.
اینها نشان دهنده ضرب کردن یک عدد در خودش هستند. بنابراین 53 یعنی
5×5×5، و2x یعنی x× xکه در اینجا x نشاندهنده یک عدد مجهول است. اینها ”مربع“،
”مکعب“ و ”بتوان چهار“ نامیده میشوند و عموماً بعنوان توان اعداد از آنها
نام برده میشود.
روش حل
معادلات درجه دوم را یونانیان، یا از بابلیان به ارث بردند، و یا دوباره خودشان
آنرا کشف کردند. هرون[50] که بین سالهای 100 ق.م و 100 ب.م در اسکندریه میزیسته، نوعی از مسائل بابلی را به سبک
یونانی مطرح کرد. حوالی سالهای 100 ب.م نیکوماکوس کتابی نوشت بنام Introductio Arithmetica (مقدمات علم حساب) که در آن از سنت یونانی، که اعداد را نشانگر کمیتهای هندسی نظیر طول یا سطح میدید، عدول کرد. از نظر نیکوماکوس اعداد نه
طول یک خط، یا مساحت یک سطح، بلکه برای خودشان کمیتهایی جداگانهای بودند. نیکوماکوس پیرو مکتب فیثاغورث بود
و آثارش این مسئله را تائید میکرد، زیر سر و کار او فقط با اعداد صحیح و کسرهای
ساخته شده از آنها بود و از علائم هم استفاده نمیکرد. اثر او، بعنوان یک کتاب درسی درباره
حساب، تا هزار سال بعد هم تدریس میشد.
نمادگرایی
و استفاده از علائم در حدود سالهای 500 ب.م با کارهای ریاضیدان یونانی دیوفانتوس[51] به جبر وارد شد. تنها چیزی که ما از دیوفانتوس میدانیم سن او
درهنگام وفاتش است که بطریقه مشکوکی به دست ما رسیده. در یک کتاب یونانی که حاوی
مسائل جبر است یکی از مسائل به این صورت طرح شده: ”دیوفانتوس یک ششم طول عمرش را
بعنوان یک پسر طی کرد. ریش او هنگامی درآمد که یک دوازدهم سنش را داشت. او پس از
اینکه یک دوازدهم دیگر از عمرش را طی کرد ازدواج نمود و پسرش پنج سال بعد بدنیا
آمد. پسرش به اندازه نصف پدر عمر کرد و مرد، پدر نیز چهار سال بعد مرد. هنگامی که
دیوفانتوس مُرد چند سال داشت؟“
شما
میتوانید با استفاده از روشهای جبر قدیم، یا روشهای جدید، نتیجه بگیرید که سن او
باید 84 سال بوده باشد. اگر فرض را بر این بگذاریم که این مسئله برمبنای واقعیت
طرح شده، که البته در آن تردید هست، باید گفت که او عمر خوبی داشته.
آنچه که
ما در مورد زندگی او میدانیم همین است. ولی مطالب زیادی درباره کتابهای او که
بعداً تکثیر، و در اسناد دیگر به آن ارجاع داده شده میدانیم. او کتابی در مورد
اعداد چندضلعی[52] دارد که قسمتهایی از آن هنوز باقی مانده است. در این کتاب که به
شیوه اقلیدسی نگاشته شده، قضایا بوسیله استدلالهای منطقی اثبات میشود و درکل از
اهمیت ریاضی خاصی برخوردار نیست. از این مهمتر، اثر 13 جلدی و قابل توجه وی بنام حساب
(Arithmetica) است که به لطف دستنویسان یونانی قرن
سیزدهم، هنوز شش جلد از آن باقی مانده. چهار جلد دیگر نیز در ایران کشف شده که
ممکن است جزیی از این اثر باشد، ولی همه دانشمندان بر این نظر نیستند که آنها
متعلق به دیوفانتوس است.
کتاب حساب
دیوفانتوس بصورت سلسلهای از مسائل ارائه شده. دیوفانتوس در مقدمه میگوید که
او این را بعنوان یک کتاب تمرین برای یکی از شاگردانش نوشته. او برای نام مجهولات
از علامت مخصوصی استفاده میکرد، و برای نشان دادن مربع و مکعب آنها نیز علائم
متفاوت دیگری را بکار میبرد که ظاهراً مخفف کلمات توان و مکعب در
زبان یونانی بودند. علامتگذاری او آنچنان ساختیافته و مرتب نبود. دیوفانتوس برای
نشان دادن جمع دو علامت، آنها را کنار هم میگذاشت (مانند همان کاری که ما امروزه
برای ضرب دو علامت میکنیم. مثلاً xy
یعنی x
ضرب در y)،
ولی برای تفریق یک علامت مخصوص داشت. او حتی علامت خاصی برای مساوی داشت، گرچه
ممکن است این علامت بعدها توسط نسخهبرداران کتابها به آن اضافه شده باشد.
کتاب حساب
عمدتاً درباره حل معادلات است. اولین جلد حل معادلات خطی را شرح میدهد؛ و پنج جلد
دیگر به حل انواع مختلف معادلات درجه دوم، که اغلب چند مجهول دارند، و نیز تعدادی
از معادلات درجه سوم ساده میپردازد. یک جنبه مهم از این کتاب این است که جواب
معادلات همیشه اعداد صحیح و یا کسری هستند. امروزه ما به معادلاتی که جواب
آنها محدود به اعداد صحیح و یا اعداد گویا باشد ”معادلات دیوفانتی“ میگوییم.
یک نمونه از معادلات کتاب حساب به این شکل است: ”سه عدد را پیدا کنید که
جمع هر سه آنها، و جمع دو به آنها با یکدیگر، یک مربع کامل باشد.“ خودتان امتحان
کنید، این مسئله اصلاً ساده نیست. جواب دیوفانتوس 41، 80 و 320 است. مجموع هر سه
آنها 441 است که 212=441. مجموع دو به دو آنها با یکدیگر هم میشود:
41+80=121=112
41+320=361=192
80+320=400=202
همانطور
که دیده میشود دیوفانتوس جواب زیرکانهای بدست داده.
امروزه
معادلات دیوفانتی در نظریه اعداد نقش محوری دارند. مثال معروف در این زمینه ”آخرین
قضیه فرما[53]“ است. که میگوید حاصل جمع دو مکعب (یا توانهای بالاتر) نمیتواند
بصورت عددی با همان توان باشد. اگر صحبت از مربع (توان دوم) باشد مسئله ساده است و
به دوران فیثاغورث باز میگردد: 52= 42+32 یا 132=122+52
. ولی شما نمیتوانید همینکار را با مکعبها (توان سوم)، توانچهارم و یا هر توان
دیگری که بزرگتر از دو باشد انجام دهید. در حدود سالهای 1650، پییر دو فرما[54] این مسئله را حدس زد و آن را در حاشیه نسخهای از کتاب حساب
دیوفانتوس که در دست داشت یادداشت کرد (البته بدون اثبات). قریب 350 سال طول کشید
تا یک ریاضیدان انگلیسی بنام اندرو ویلس[55] اثبات کند که حدس فرما درست بوده.

در حقیقت
جبر در سال 830 میلادی، و در زمانی که جنبش اصلی از سرزمین یونان به دنیای عرب
جابجا شد، به صحنه ریاضیات وارد شد. در آن سال، منجمی بنام محمدابن موسی الخوارزمی
کتابی نوشت بنام الجبر و المقابله، که ترجمه تحتالفظی آن میشود
”بازگردانی و سادهسازی“. این لغات به روشهای معینی برای دستکاری معادلات اشاره میکنند
که با کاربرد آنها میتوان معادلات را بصورت مناسبتری درآورد تا راحتتر حل شوند.
لغتی که حالا ما به آن جبر میگوییم، از نام همان کتاب، یعنی الجبر
والمقابله گرفته شده. اولین ترجمه این کتاب به زبان لاتین در قرن یازدهم میلادی و
تحت عنوان Ludus
Algebrae et Almucgrabalaeque انجام گرفت.
کتاب
خوارزمی در بر دارنده نکاتی است که تحت تاثیر ریاضیات بابلی و یونانی نوشته شده.
علاوه بر آن ایدهایی که در حوالی سالهای 600 میلادی در هندوستان بوسیله
براهماگوپتا ابداع شد نیز در آن آمده. در این کتاب شرح داده میشود که چگونه
معادلات خطی و درجه دوم را حل کرد. به فاصله اندکی جانشینان خارزمی روشهایی برای
حل برخی از معادلات درجه سوم پیدا کردند. از میان آنها میتوان به ثابت بن قره،
طبیب، منجم، و فیلسوف که در بغداد زندگی میکرد و حسن بن هیثم، که عموماً در غرب
بنام الهازن شناخته میشود، اشاره کرد. ولی مشهورترین آنها عمر خیام است.
نام کامل
عمر خیام طولانی است: غیاثالدین ابوالفتح عُمَر بن ابراهیم خیام نیشابوری. کلمه
خیام بصورت لفظی به معنی ”چادر ساز“ است که برخی از تاریخ نگاران عقیده دارند ممکن
است شغل پدرش ابراهیم بوده باشد. خیام در سال 1047 میلادی (427 شمسی) در ایران
بدنیا آمد و بیشتر عمر پربارش را در نیشابور سپری کرد. نیشابور شهری در نزدیکی
مشهد در استان خراسان و نزدیک مرزهای ترکمنستان است.
در افسانهها آمده که خیام در جوانی موطن خویش را به
قصد نیشابور ترک کرد تا نزد امام موفق نیشابوری به تحصیل
علوم دینی بپردازد. در آنجا او با دو همشاگردی دیگرش، یعنی حسن صباح و
نظامالملک عهدی را بستند
مبنی بر اینکه هرکدام از آنها که به ثروت یا شهرت رسیدند باید آنرا با دو نفر دیگر
قسمت کنند. اصطلاح سه یار دبستانی از همینجا ریشه میگیرد: خیام، نظامالملک، و
حسن صباح.
سه رفیق
تحصیلاتشان را تمام کردند و
سالها گذشت و عهد بر سر جایش باقی بود. نظامالملک به کابل رفت، خیام که از نظر سیاسی
جاهطلبی کمتری داشت مدتی به
خیمه سازی پرداخت ولی چون اشتیاق او به علم و ریاضیات بود بیشتر اوقات بیکاریش را صرف آنها میکرد. سرانجام نظامالملک که برای خود جایگاهی در دربار آلب
ارسلان کسب کرده بود از سفر بازگشت. او پس از مدتی به مقام وزیری رسید.
بدلیل
اینکه حالا نظامالملک
برای خود شخص معروف و ثروتمندی بود، خیام و حسن صباح عهد دیرین را به او یادآوری
کردند. نظامالملک
از سلطان اجازه خواست تا به دوستانش یاری رساند، و هنگامی که درخواست او از طرف
سلطان اجابت شد او به عهد خود وفا کرد. حسن صباح یک منصب خوب دولتی گرفت، ولی خیام
تنها مشتاق ادامه تحقیقات علمی خود در نیشابور بود، جایی که بتواند ممنون نظامالملک باشد. از این روی نظامالملک برای او یک مستمری دولتی معین کرد تا
وی بتواند به تحقیقات خود بپردازد. و با اینکار به وعده خود عمل کرد.
بعدها،
حسن صباح سعی کرد تا یک صاحب منسب بلند پایه دولتی را از کار براندازد و بخاطر
همین، کارش را از دست داد. ولی خیام در آرامش به کار خود ادامه داد و به سرپرستی
هیئتی منصوب شد که ماموریت آن اصلاح تقویم ایرانی بود. تقویم ایرانی بر پایه حرکت
خورشید بود، و اولین روز سال نو هر بار تغییر میکرد، که این مسئله موجب سردرگمی بود. این
کار تنها از دست یک ریاضیدان شایسته برمیآمد، و خیام با بکار بردن دانش خود از
ریاضیات و نجوم توانست با محاسبات خود تقویم را اصلاح کند و مشخص سازد که روز اول
یک سال مفروض را چه موقع باید نادیده گرفت.
در حوالی
همین سالها بود که او رباعیات را بنگارش درآورد. رباعی نوعی شعر است که
دارای چهار مصراع میباشد،
که به جز مصرع سوم، همه آنها هم قافیهاند. و رباعیات مجموعه شعرهای رباعی است:
چون عمر بسر رسد چه بغداد و چه
بلخ
پیمانه چو پر شود چه شیرین و چه تلخ
خوش باش که بعد از من و تو
ماه
سی از سلخ به غره آید از غره به سلخ
اي دوست، بيا تا غم فردا
نخوريم
وين يک دم عمر را غنيمت شمريم
فردا چو از اين دير
فنا در
گذريم با
هفت هزار سالگان همسفريم
درهمین
حال، حسن صباح که مغضوب شده بود مجبور شد نیشابور را ترک کند و بدام راهزنانی
افتاد که از دانش او استفاده کرده و سرانجام پس از مدتی او را به رهبری خود
برگزیدند. در سال 1090 میلادی راهزنان به فرمان حسن صباح قلعه الموت را که در رشته
کوههای البرز قرار دارد به تصرف خود درآوردند. آنها مردم آن نواحی را مرعوب کردند
و از آن موقع به بعد حس صباح به پیرمرد کوهستان بدنام شد. پیروان او که بدلیل
استفاده از مواد مخدر به هشیشیون معروف بودند، برای خود در دل کوهستان
استحکاماتی را درست کردند تا پس از ترور شخصیتهای سیاسی و مذهبی در آنجا مخفی
شوند. نام آنها (هشیشیون) ریشه لغت assassin
”اَسَسین“ به معنی کشتن و ترور کردن است. از این روی حسن صباح هم بنوبه خود مشهور
و ثروتمند شد.
در حالیکه
خیام مشغول محاسبه جداول نجومی و پیدا کردن راههایی برای حل معادلات درجه سوم بود،
نظامالملک مسیر زندگی سیاسی خود را دنبال کرد، تا اینکه از قضای روزگار توسط
فدائیان حسنصباح بقتل رسید. خیام تا 76 سالگی زندگی کرد، و بنا به روایاتی در سال
1123 میلادی (510 شمسی) در گذشت. حسن صباح نیز که به سن 84 سالگی رسیده بود در
همان سال درگذشت. هشیشیون (فدائیان) به مبارزه خود با نظام سیاسی ادامه دادند تا
اینکه سرانجام در سال 1256 میلادی بدست مغولهایی که قلعه الموت را تصرف کردند
ریشهکن شدند.

به کارهای
ریاضی خیام بازگردیم: مورخین عقیده دارند در حدود سال 350 ق.م، ریاضیدان یونانی
مناکئوس، منحنیهای
خاصی بنام ”مقاطع مخروطی“ را کشف کرد که از آنها برای دو برابر کردن مکعب استفاده
میکرد. ارشمیدس مبانی نظری
این منحنیها را
بسط داد و نهایتاً آپولونیوس[56] از اهالی پرگا، در کتاب معروفش بنام مقاطع
مخروطی این مبحث گسترش داد و آنرا بصورت نظاممند درآورد. آنچه در نظر خیام جالب آمد، کشف
این مسئله توسط یونانیها بود
که چگونه مقاطع مخروطی میتوانند برای حل برخی از معادلات درجه سوم بکار روند.
این نوع
منحنیها به این دلیل مقاطع مخروطی نامیده میشوند که میتوان آنها را با قطع کردن
مخروط با یک صفحه بدست آورد. اگر بخواهیم دقیقتر بیان کنیم، بجای مخروط باید
بگوئیم مخروط مضاعف، که شکل آن مثل دو بستنی قیفی است که از ته به یکدیگر وصل شده
باشند. یک مخروط ساده از مجموعهای از پارهخطها تشکیل میشود که از یک دایره، که
آنرا قاعده مخروط مینامیم، عبور کرده و همدیگر را در یک نقطه قطع میکنند. ولی در
نظر یونانیها شما همیشه میتوانید پارهخطها را از این نقطه امتداد دهید و نتیجه
یک مخروط مضاعف حاصل کنید.
سه نوع از
مقاطع مخروطی اصلی عبارتند از: بیضی، سهمی و هذلولی. بیضی یک منحنی تخممرغی شکل
بسته است که هنگامی حاصل میشود که صفحه تنها یکی از مخروطها را قطع کند (دایره
نوعی از بیضی است که هنگامی حاصل میشود که صفحه قطع کننده بر محور مخروط عمود
باشد).
یک هذلولی متشکل از دو منحنی متقارن شبیه به هم است
که اساساً تا بینهایت امتداد یافته و هنگامی حاصل میشود که صفحه قطع کننده از هر
دو مخروط عبور کند. سهمی نوعی فرم انتقالی است که از یک منحنی باز تشکیل شده و
صفحه قطع کننده با یکی از خطوطی که سطح مخروط را تشکیل میدهند موازی است.
مقاطع مخروطی
جدا از
هندسه اقلیدسی، مطالعات گسترده هندسهدانان یونانی در مقاطع مخروطی یکی از مهمترین
حوزههای پیشرفت آنها در ریاضیات بحساب میآید. این منحنیها هنوز هم جزء بخش
بسیار مهمی از ریاضیات امروزی باقی ماندهاند، ولی بدلیلی کاملاً متفاوت از آنچه
برای یونانیان جذاب بود. این منحنیها از نقطه نظر جبری، پس از خطوط صاف، سادهترین
منحنیها محسوب میشوند. آنها همچنین در علومکاربردی اهمیت زیادی دارند. مثلاً
کپلر از مشاهدات تیکو براهه نتیجه گرفت مدار سیارات در منظومه شمسی بیضی شکل
هستند. این مدار بیضیشکل یکی از مشاهداتی را تشکیل میدهد که باعث شد نیوتون
قانون معروف ”مربع معکوس[57]“ را برای گرانش فرمولبندی کند. این بنوبه
خود، موجب درک این واقعیت شد که برخی از جنبههای جهان، بطور وضوح از خود الگوهای
ریاضی بروز میدهند.

عمده آثار
ریاضی باقیمانده از خیام به نظریه معادلات اختصاص دارد. او دو راه حل را مد نظر
داشت. روش اول از سنت دیوفانتوس پیروی میکرد و تنها اعداد صحیح را بعنوان
جواب درنظر میگرفت. او این روش را ”جبری“ مینامید، هرچند ”حسابی“ صفت
مناسبتری برای این روش است تا ”جبری“. دومین نوع راهحل، که او آنرا ”هندسی“ مینامید
روشی بود که در آن جواب معادله از روی طول، سطح و یا حجم اشکال هندسی تعیین میشد.
با آزادی
عملی که خیام در استفاده از مقاطع مخروطی داشت، توانست روشهایی برای حل کلیه
معادلات درجه سوم ابداع کند، و آنها را در کتابی بنام جبر که در سال 1079
میلادی چاپ کرد شرح داد. بدلیل اینکه در آن دوران هنوز اعداد منفی شناخته نشده
بود، همیشه معادلات را طوری مرتب میکردند که جملات آن از اعداد مثبت تشکیل شود.
این نوع قاعده موجب شد تا تعداد زیادی از حالات برای معادله بوجود آید، که امروزه
همه آنها اساساً در قالب یک نوع معادله بیان میشوند، با این تفاوت که جملات
معادله میتواند اعداد مثبت یا منفی باشند. با در نظر گرفتن اینکه کدام جمله در
کدام طرف معادله ظاهر شود، خیام چهارده حالت مختلف برای معادله درجه سوم
قائل شد. وی حالات مختلف معادله درجه سوم را بصورت زیر طبقه بندی کرد:
مکعب
= مربع + طول + عدد
مکعب
= مربع
+ عدد
مکعب = طول + عدد
مکعب
= عدد
مکعب
+ مربع
= طول
+ عدد
مکعب + مربع = عدد
مکعب + طول = مربع + عدد
مکعب + طول = عدد
مکعب + عدد = مربع + طول
مکعب + عدد = مربع
مکعب + عدد = طول
مکعب + مربع + طول = عدد
مکعب + مربع + عدد = طول
مکعب + طول + عدد = مربع
که هریک از جملات فهرست فوق نشاندهند یک ضریب عدد مثبت در معادله است. شما ممکن است با خودتان فکر کنید که چرا فهرست بالا شامل معادلاتی نظیر معادله زیر نیست:
مکعب
+ مربع
= طول
دلیل این
امر این است که ما میتوانیم دو طرف این معادله را بر مجهول تقسیم کنیم و آنرا به
یک معادله درجه دوم تنزل دهیم. بعبارت دیگر معادله بالا درجه سوم نیست بلکه درجه
دوم است.
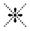
خیام
بتنهایی این راهحلها را ابداع نکرد، درعوض آنها را برپایه کارهای اولیه یونانیان
قرار داد که با استفاده از مقاطع مخروطی توانسته بودند برخی معادلات درجه سوم را
حل کنند. او ایدههای خود را بصورت نظامندی بسط داد و توانست تمام چهارده نوع
معادله درجه سوم را حل کند. او در کتاب خود اشاره میکند که ریاضیدانان پیشین
روشهایی را برای حل برخی از حالتهای خاص پیدا کرده بودند، ولی این روشها خیلی خاص
بود، بدلیل اینکه هر حالت از معادله راهحل خاص خودش را میطلبید؛ هیچکس قبل از او
حالت کلی معادله درجه سوم را بررسی نکرده بود، چه رسد راهحلهایی برای آنها ابداع
کند. وی مینویسد: ”برخلاف بقیه، من هیچگاه از تلاش برای شناختن حالتهای مختلف
اینگونه معادلات و اینکه کدامیک ممکن هستند و کدام ناممکن، دست برنداشتم.“
منظور او از ”ناممکن“ این بود که معادله هیچ گونه جواب مثبتی نداشته باشد.
بمنظور
اینکه کمی با حال و هوای کارهای او اشنا شوید در اینجا من چگونگی راهحل او برای
یکی از معادلات بالا ذکر میکنم. مثلاً معادله آخری یعنی ” مربع=عدد+طول+مکعب“ را
درنظر بگیرید که ما در فرم امروزی آنرا بصورت زیر مینویسیم:
x3 + bx + c = ax2
(بدلیل
اینکه امروزه اعداد مثبت و منقی برای ما فرقی ندارند، میتوانیم جمله ax2 را بسمت چپ معادله
ببریم و علامت آنرا از a به a- تغییر دهیم تا معادله بشکل x3 - ax2 +
bx + c = 0 درآید).
خیام به
خوانندگان خود میگوید مراحل زیر را بترتیب انجام دهند:
با استفاده از یک مثلث قائمالزاویه سه پارهخط
بسازید که طول آنها برابر c/b,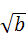 , a باشد. (2) یک نیمدایره
رسم کنید که قطر آن خط افقی پرنگ حاصل از مرحله قبل باشید. خط عمود که طول آن
, a باشد. (2) یک نیمدایره
رسم کنید که قطر آن خط افقی پرنگ حاصل از مرحله قبل باشید. خط عمود که طول آن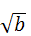 بود
را امتداد دهید تا آنرا قطع کند. اگر طول خط عموی پرنگ d باشد، خط افقی پرنگ را طوری بسازید که طول آن برابر با cd/
بود
را امتداد دهید تا آنرا قطع کند. اگر طول خط عموی پرنگ d باشد، خط افقی پرنگ را طوری بسازید که طول آن برابر با cd/
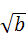 باشد.
(3) یک هذلولی رسم کنید (منحنی پررنگ) که خطوط مجانبی آن (آن خطوطی که هر چه منحنی
امتداد پیدا میکند به آنها نزدیکتر میگردد) خطوط سایه نقطه چین باشند که از نقطه که
قبلا ساخته شد عبور کند. (4) نقطهای را که در آن هذلولی نیم دایره را قطع میکند پیدا
کنید. آنگاه طول دو خط پررنگ که با x نشان داده شده هر دو جواب (مثبت) معادله
درجه سوم هستند.
باشد.
(3) یک هذلولی رسم کنید (منحنی پررنگ) که خطوط مجانبی آن (آن خطوطی که هر چه منحنی
امتداد پیدا میکند به آنها نزدیکتر میگردد) خطوط سایه نقطه چین باشند که از نقطه که
قبلا ساخته شد عبور کند. (4) نقطهای را که در آن هذلولی نیم دایره را قطع میکند پیدا
کنید. آنگاه طول دو خط پررنگ که با x نشان داده شده هر دو جواب (مثبت) معادله
درجه سوم هستند.
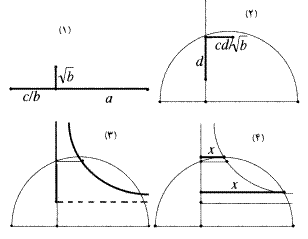
روش خیام برای حل معادلات درجه سوم
همانطور
که گفتم جزئیات اینکار، در مقابل اصول انجام آن، از اهمیت کمتری برخوردار است. مثل
همیشه با استفاده از خط کش و پرگار عمل میکنیم، چند خط و دایره رسم میکنیم، یک هذلولی
میکشیم، باز هم چند قاعده اقلیدسی دیگر را بکار میبریم و نهایتاً کار تمام میشود.
خیام راهکارهای
مشابهای برای حل هریک از چهارده حالت ارائه میدهد و آنها را اثبات میکند. تجزیه
و تحلیل او چند نقص کوچک دارد: هنگامی که ضرایب معادله یعنی a, b, c بطور غیر
مناسبی انتخاب شوند، نقاطی که برای روش او لازم است وجود خارجی پیدا نمیکنند.
برای نمونه در معادله قبلی ممکن است هذلولی اصلاً نیمدایره را قطع نکند. ولی
گذشته از این خردهگیریهای نابجا، کاری که او انجام داد حقیقتاً تحسینبرانگیز و
بسیار نظاممند بود.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
”من به
کتاب مقدس خدا قسم میخورم، که اگر شما کشفیات خود را به من یاد دهید، نه فقط هیچ
موقع آنها را چاپ نمیکنم، بلکه بعنوان یک مرد باشرف مسیحی قول میدهم تنها بصورت
رمزی از آنها یادداشت بردارم تا پس از مرگم کسی نتواند آنها را بفهمد.“
از قرار
معلوم این یک سوگندنامه رسمی است که در سال 1539 نوشته شده.
ایتالیا
در دوران رنسانس سرمنشاء اختراعات در علوم مختلف بود و در این میان ریاضیات هم
استثنا نبود. در فضای ساختارشکن آن دوران، ریاضیدانان عصر رنسانس مصمم بودند که به
محدودیتهای ریاضیات سنتی فائق آیند. یکی از آنها پیدا کردن راهحل معادلات مرموز
درجه سوم بود. حالا یک ریاضیدان، دیگری را به دزدی اسرارش متهم میکند.
ریاضیدان
خشمگین نیکولا فونتانا معروف به تارتالیا[58] بود. کسی که متهم به سرقت این اثر علمی شده
بود، ریاضیدان، پزشک، قمارباز کهنهکار، و فردی دغلباز بود. نام او جرلامو
کاردانو[59] معروف به جروم کاردان[60] بود. کاردانو که در کودکی یک نابغه واقعی
بود، در حدود سال 1520 پا در جای پدرش گذاشت و مانند او ورشکسته شد! از آن پس او
برای امرار معاش به قمار روی آورد و از دانش ریاضی خود برای محاسبه شانس برنده شدن
استفاده میکرد. او همیشه با همراهانش درگیر بود؛ روزی به یکی از بازیکنان که تقلب
میکرد مظنون شد و چنان با پهنه چاقو به صورت وی کوفت که او را زخمی کرد.
آن زمان
دوران سختی بود و کاردانو نیز مرد قویی هیکلی بود. او همچنین متفکر اصیلی هم بود
که یکی از مشهورترین و تاثیرگذارترین متون جبر را در تاریخ نوشت.

ما مطالب
زیادی را درباره کاردانو میدانیم زیرا او در سال 1575 کتاب زندگینامهاش را برای
ما بجای گذاشت. مانند بسیاری از ریاضیدانان همعصر خودش، کاردانو به کار طالعبینی
نیز وارد بود. وی وضعیت صور فلکی را در هنگام تولدش چنین توصیف میکند:
”آنگونه
که شنیدهام، باوجود اینکه به مادرم داروهای مختلفی برای سقط جنین داده
بودند، در هنگامی که از اولین ساعت شب کمی بیشتر از نیم ساعت، ولی کمتر از
سهربع ساعت گذشته بود، من بصورت طبیعی در 24 سپتامبر سال 1500 میلادی متولد شدم
... بواسته عدم سازگاری مکانی، مریخ سایه نحسش را بصورت یک چهار گوشه بر روی ماه
افکنده بود.
بلاخره من
بدنیا آمدم، بهتر بگویم بسختی از رحم مادرم بیرون کشیده شدم؛ تقریباً مرده بودم.
موهایم سیاه و مجعد بود. مرا در یک تشت مملو از شراب گرم شستشو دادند، چیزی که
میتوانست برای هر نوزاد دیگری کشنده باشد. مادرم به مدت 3 روز کامل زیر زایمان درد
میکشید و با اینحال من جان سالم بدر بردم.“
در فصلی
از کتاب زندگی من، کاردانو به فهرست کتابهایی که نوشته اشاره میکند. اولین
آنها در این فهرست کتاب ”هنر عظمی“ است که یکی از سه رسالهایست که
او در باره موضوعات ریاضی تحریر کرده. او کتابهایی درباره نجوم، فیزیک، اخلاق،
سنگشناسی، آب، پزشکی، فالگویی و الهیات نیز نوشته است.
در اینجا
تنها کتاب ”هنر عظمی“ است به داستان ما مربوط میشود، و این را از عنوان
فرعی کتاب که ” قواعد جبر“ است میتوان بخوبی فهمید. در این کتاب کاردانو نه
فقط روشهایی برای حل معادلات درجه دوم، که بر بابلیان نیز شناخته شده بود گردآوری
کرده، بلکه روشهایی برای حل معادلات درجه سوم و چهارم نیز ابداع کرد. برخلاف روش
خیام که به هندسه مقاطع مخروطی تکیه داشت، روشهای ذکر شده در کتاب ”هنر عظمی“
صرفاً جبری هستند.
پیشتر من
به دو علامت ریاضی که در عباراتی نظیر x3 میبینیم اشاره کردم. اولین
آنها علامتی است که با یک حرف (در اینجا x) آنرا نمایش میدهیم و نشان
دهنده یک عدد مجهول است. دومی اعداد کوچکی هستند که بصورت بالانویس نوشته میشوند
و نشان دهنده توان هستند. بنابراین، مثلاً x3، که نشاندهنده مکعب x است، یعنی x ×x×x.
سومین نوع
علامت که ما با آن سروکار داریم، خیلی زیباست و شبیه به این است: 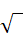 .
این علامت که رادیکال نامیده میشود، بمعنای ”ریشه دوم“ یا جذر است. برای مثال
.
این علامت که رادیکال نامیده میشود، بمعنای ”ریشه دوم“ یا جذر است. برای مثال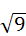 یعنی
ریشه دوم عدد 9، که یعنی همان عددی که وقتی درخودش ضرب شود حاصل 9 میشود. بدلیل
اینکه 3 × 3 میشود 9 پس 3=
یعنی
ریشه دوم عدد 9، که یعنی همان عددی که وقتی درخودش ضرب شود حاصل 9 میشود. بدلیل
اینکه 3 × 3 میشود 9 پس 3= 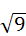 .
این قضیه همیشه هم به این سادگی نیست. بدنامترین ریشه دوم، که بر اساس یک داستان
غیرمحتمل باعث شد یک ریاضیدان را از کشتی به دریا انداخته شود، جذر عدد 2 یعنی
.
این قضیه همیشه هم به این سادگی نیست. بدنامترین ریشه دوم، که بر اساس یک داستان
غیرمحتمل باعث شد یک ریاضیدان را از کشتی به دریا انداخته شود، جذر عدد 2 یعنی 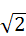 است.
مقدار اعشاری این عدد هرگز بپایان نمیرسد و چیزی شبیه این است:
است.
مقدار اعشاری این عدد هرگز بپایان نمیرسد و چیزی شبیه این است:
1.4142135623730950488
ولی ریشه
دوم عدد 2 نمیتواند به اینجا ختم شود، زیرا مربع عدد بالا میشود:
1.99999999999999999999522356663907438144
که معلوم
است با عدد 2 تفاوت دارد.
این بار
ما میدانیم که علامت 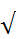 از
کجا آمده. این علامت شکل کج شده حرف r
است که از لغت ”radix“
گرفته شده و در زبان لاتین به معنای ”ریشه“ است. ریاضیدانان نیز از همین معنی
استفاده میکنند و
از
کجا آمده. این علامت شکل کج شده حرف r
است که از لغت ”radix“
گرفته شده و در زبان لاتین به معنای ”ریشه“ است. ریاضیدانان نیز از همین معنی
استفاده میکنند و 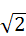 را
”ریشه دوم“ (یا جذر) عدد 2 میخوانند.
را
”ریشه دوم“ (یا جذر) عدد 2 میخوانند.
ریشههای
سوم، چهارم، پنجم و غیره نیز به این شکل نشان داده میشوند و عدد ریشه را ما بین
دهانه علامت √ قرار میدهیم:
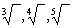
ریشه سوم
یک عدد مفروض عبارت است از عددی که اگر آنرا سه بار در خودش ضرب کنیم، حاصل عدد
مفروض ما شود. بنابراین ریشه سوم عدد 8 میشود 2 زیرا 8=23 . دوباره
تکرار میکنم، مانند ریشه دوم، ریشه سوم عدد 2 (یعنی 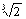 )
نیز میتواند بصورت یک عدد اعشاری و بصورت تخمینی بیان شود. مثلاً میتوان 19 رقم اول
آنرا بصورت زیر نمایش داد:
)
نیز میتواند بصورت یک عدد اعشاری و بصورت تخمینی بیان شود. مثلاً میتوان 19 رقم اول
آنرا بصورت زیر نمایش داد:
...
1.2599210498948731648
و همانطور
که گفته شد این عدد هم پایانی ندارد و تا هر قدر که بخواهیم میتوانیم آنرا دقیقتر
محاسبه کنیم. همین عدد بود که برای یونانیان باستان (در مورد نصف کردن مکعب) به یک
مشکل بدل شده بود.

از سال
400 میلادی به بعد، ریاضیات یونانی دیگر در رده پیشگامان دانش محسوب نمیشد.
فعالیتهای ریاضی به شرق منتقل شده بود، به شبه جزيرهي عربستان، هند و
چین. اروپا به ”دوران تاریک“ خود نزول کرده بود، و هر چند این دوران
به آن تاریکی که برخی مورخین توصیف میکنند نبود، ولی بااینحال به اندازه کافی
تاریک بود. گسترش مسیحیت تاثیر شومی بر یادگیری و تحقیق در کلیساها و صومعهها
گذاشته بود. بسیاری از راهبان در صومعههای خود از آثار ریاضیدانان برجستهای
همچون اقلیدس کپی برمیداشتند، ولی فقط تعداد اندکی از آنها، آنچه را که از آن
رونوشت برمیداشتند میفهمیدند. اگر بخواهیم مقایسهای از دوران پرشکوه یونان و
عصر تاریک داشته باشیم باید بگوییم یونانیان باستان میتوانستند از دو سوی یک کوه
تونلی حفر کنند تا در میانه به هم برسند؛ درمقابل در نظر قوم آنگلو-ساکسون اولیه،
مساحی و طراحی چیزهایی بودند که باید در مقیاس حقیقی روی زمین انجام میشد. حتی
مفهوم رسم در مقیاس کوچکتر نیز از اذهان رفته بود. اگر آنگلو-ساکسونها میخواستند
از انگلستان یک نقشه دقیق رسم کنند، این نقشه باید به اندازه خود انگلستان میبود!
آنها نقشههایی در ابعاد معمول نیز کشیده بودند ولی خیلی دقیق نبودند.
از اواخر
قرن پانزدهم میلادی، باردیگر کانون فعالیتهای ریاضی متوجه اروپا شد. همانگونه که
خاور دور و میانه رمق خلاقانه خود را از دست دادند، در اروپا، که تلاش میکرد از
زیر سلطه کلیسای روم خلاصی یابد، نسیم تازهای دمیدن گرفت. در همان حالی که روم
کنترلش را بر روی حیاط خلوت خود از دست میداد، بطور طعنهآميزی ایتالیا به مرکزی
برای فعالیتهای روشنفکری آن زمان بدل گشت.
تغییرات
عمده در علم و ریاضیات اروپا، با چاپ کتابی در سال 1202 میلادی آغاز شد. نام کتاب Liber Abbaci (کتاب چرتکه) بود که
توسط لئوناردو پیزا، که به نام مستعارش یعنی فیبوناچی[61] معروف است، نوشته شد. گیولرمو، پدر لئوناردو
کارمند اداره گمرک بوجیا (الجزایر کنونی) بود. شغل وی طوری بود که با مردمانی از
فرهنگهای مختلف در تماس بود. او سیستم جدید نمایش اعداد، متشکل از ده رقم 0 تا 9،
که توسط هندیها و اعراب اختراع شده بود را به پسرش آموخت. لئوناردو بعدها نوشت
”من بقدری از این روش لذت بردم که درحالی که برای امور تجاری خودم به مصر،
سوریه، یونان، سیسیل و بلاد دیگر سفر میکردم به ادامه تحصیل ریاضیات پرداختم و در
آنجا با علمای محلی بحثهای لذتبخشی داشتم.“
در نگاه
اول بنظر میرسد که کتاب لئوناردو درباره چرتکه باشد. چرتکه وسیلهای قدیمی برای
حساب کردن است. ولی همانگونه که لغت calculus،
که به معنای سنگ ریزه است، بعدها معانی گوناگونی پیدا کرد (مثلاً برای نامیدن شاخه
حسابان ریاضی از آن استفاده میکنیم)، لغت abbaco هم که به معنای چرتکه است، برای اشاره به هنر محاسبه
بکار گرفته شد. ”Liber Abbaci“
اولین کتابی بود که سیستم عدد نویسی هندی-عربی را به اروپا آورد. قسمت اعظم کتاب
به کاربرد حساب جدید در امور روزمرهای همچون محاسبه تبادلات ارزی اختصاص دارد.
اکنون
مسئله خاص در این کتاب وجود دارد که بعدها موجب شهرت فراوانی برای فیبوناچی شد.
این مسئله که در مورد چگونگی رشد ایدآل خرگوشها است، به دنباله جالبی از اعداد
1, 1, 2, 3, 5, 8, 13, 21, 34, 55 و غیره منتهی میشود، که هر
یک از این اعداد (از سومی به بعد) حاصل جمع دو عدد قبلی است. این سلسله از اعداد
که به ”دنباله فیبوناچی[62]“ معروف است، نه بدلیل مطالعه رشد جمیت خرگوشها،
بلکه بخاطر الگوی ریاضی مهمی که از آن پیروی میکند، و نیز بدلیل نقش کلیدی که در
نظریه اعداد گنگ بازی میکند، از اهمیت فراوانی در ریاضیات برخوردارند. لئوناردو
هیچگاه فکر نمیکرد که این نکته بامزه درمورد خرگوشها به چنان مسلئه مهمی بدل شود
که بر بقیه آثارش چنان سایه گستردهای بیافکند.
لئوناردو
کتابهای متعدد دیگری هم نوشت، که از آن میان میتوان به Practica Geometriae یا هندسه عملی اشاره کرد. این کتاب که در سال 1220 نگاشته
شد حاوی قسمت اعظمی از کتاب اقلیدس و نیز اندکی مثلثات یونانی میباشد. کتاب دهم
از مجموعه اصول اقلیدس اعداد گنگی را بررسی میکند که حاوی دو ریشه دوم تودرتو
شبیه به 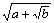 هستند. لئوناردو ثابت کرد که اینگونه از
اعداد گنگ برای حل معادلات درجه سوم کافی نیستند. این مسئله به این معنا نیست که
ریشه سوم نمیتواند توسط خطکش و پرگار ساخته شود، زیرا ترکیبات دیگری از ریشه دوم
ممکن است این را حل کند. ولی این اولین باری بود که به این مسئله اشاره میشد که
معادلات درجه سوم نمیتوانند تنها با استفاده از ابزارهای اقلیدسی حل شوند.
هستند. لئوناردو ثابت کرد که اینگونه از
اعداد گنگ برای حل معادلات درجه سوم کافی نیستند. این مسئله به این معنا نیست که
ریشه سوم نمیتواند توسط خطکش و پرگار ساخته شود، زیرا ترکیبات دیگری از ریشه دوم
ممکن است این را حل کند. ولی این اولین باری بود که به این مسئله اشاره میشد که
معادلات درجه سوم نمیتوانند تنها با استفاده از ابزارهای اقلیدسی حل شوند.
در سال
1494 لوکا پاتچولی[63] قسمت اعظم دانش ریاضی موجود آن زمان، شامل
حساب، هندسه، و تناسبات را در یک مجموعه قرار داد. زمینه اصلی کتاب به موضوعاتی
چون طراحی در طبیعت (که در تناسبات تجلی پیدا میکند)، بدن انسان، ژرفانمایی
(پرسپکتیو) در هنر و نظریه رنگها میپرداخت.
پاتچولی
سنت جبر ”بیانی“ را ادامه داد و بجای علامتها از الفاظ استفاده میکرد. نام مجهول
”چیز“ بود که در ایتالیایی به آن cosa
میگویند و به همین خاطر به کسانی که جبر کار میکردند ”کوسیست“ میگفتند. او
همچنین برخی از مخففسازیهایی که دیوفانتوس پیشگام آن بود را اتخاذ کرد (البته
بدون اینکه آنها را بهبود بخشد). موریس کلاین[64] در کتاب بیادماندنی خود بنام اندیشه
ریاضی از عهد باستان تا دوران جدید به نکته جالبی اشاره میکند و میگوید
”کتاب پاتچولی شرحی است بر توسعه ریاضیات مابین سالهای 1200 تا 1500 میلادی، و
باید گفت محتوای این کتاب بسختی بیش از آن است که فیبوناچی در کتاب Liber abbaci آورده. درحقیقت
حساب و جبر ... همه برپایه کتاب فیبوناچی بنا شده بودند.“
در انتهای
کتابش پاتچولی به این مسئله اشاره میکند که فهمی که از حل معادلات درجه سوم موجود
است چیزی بهتر از آنچه در مورد مسئله تربیع وجود دارد نیست. ولی همانطور که خواهیم
دید، این نظر بزودی تغییر میکند. چندی بعد، اولین پیشرفت غیر منتظره در شهر
بولونیا روی میدهد. چیزی که در ابتدا کسی متوجه آن نمیشود.

جرلامو
کاردانو فرزند نامشروع وکیلی بنام فایزو کاردانو بود. مادرش زن جوان و تازه بیوه
شدهای بنام کیارا میچریا بود که از ازدواج قبلیاش سه فرزند داشت. کاردانو در
پاویا، شهری در دوک نشین میلان، در سال 1501 زاده شد. هنگامی که طاعون به میلان
آمد، خانواده کیارا وی را که بر سر جرلامو حامله بود ترقیب کردند که به روستاهای
اطراف برود و در آنجا وضع حمل کند. سه بچه دیگر او که همراهش نبودند همگی از طاعون
تلف شدند.
جرلامو در
اتوبیوگرافی خود مینویسد:
”پدرم
همیشه ردایی ارغوانی رنگ بتن داشت، جامهای که در اجتماع ما مرسوم نبود؛ او هیچوقت
بدون عرقچین سیاهی که بر سر میگذاشت دیده نمیشد ... از سن پنجاه وپنج سالگی به
بعد تمام دندانهایش را از دست داد. او بخوبی با آثار اقلیدس آشنایی داشت؛ درواقع
آنقدر مطالعه میکرد که شانههایش گرد شده بودند ... مادرم خیلی زود برانگیخته میشد؛
هوش و حافظه خوبی داشت، زنی بود مذهبی با اندامی کوچک و فربه.“
گرچه
فازیو، پدر جرلامو ، یک وکیل بود، ولی آنقدر در ریاضیات مهارت داشت تا به لئوناردو
داوینچی[65] در مورد هندسه مطالبی را بیاموزد. او در دانشگاه پاویا[66]، و همچنین در بنیاد پیاتی، هندسه تدریس میکرد. او به پسر
نامشروعش جرلامو نیز ریاضی درس میداد.
”در اوان
کودکی پدرم به من اصول حساب را یاد داد، و در همان ایام مرا با علوم سری آشنا
ساخت؛ بعد از آن اصول طالعبینی عربی را به من آموخت ... پس از اینکه دوازده ساله
شدم، شش جلد اول کتاب اصول اقلیدس را به من یاد داد.“
جرلامو از
کودکی مشکل سلامتی داشت؛ تلاشهایی که برای درگیر کردن او در کسب و کار خانوادگی
صورت میگرفت ناموفق بود. جرلامو پدرش را متقاعد کرد که به او اجازه دهد در
دانشگاهی که خودش درس میداد به تحصیل پزشکی بپردازد. البته پدرش حقوق را ترجیح میداد.
در سال
1494 میلادی، چارلز هشتم پادشاه فرانسه به ایتالیا حمله کرد، و جنگهایی که بدنبال
آن آمد، بمدت پنجاه سال بصورت پراکنده ادامه یافت. بروز درگیریها موجب بسته شدن
دانشگاه پاویا شد و جرلامو مجبور شد برای ادامه تحصیل به پادوآ نقل مکان کند. از
تمام جهات وی یک شاگر اول محسوب میشد و هنگامی که فازیو مُرد، جرلامو درگیر
مبارزات انتخاباتی برای نشستن در جایگاه رئیس دانشگاه بود. گرچه بسیاری از مردم
بدلیل اینکه وی به صراحت عقایدش را مطرح میکرد از او بیزار بودند، ولی بااینحال
او تنها با اختلاف یک رای به این مقام منصوب شد.
این زمان
مصادف با هنگامی است که او میراث خودش را به هدر داد و به قمار روی آورد، مشکلی که
تا آخر عمر متلاطمش در آن گرفتار بود. و تنها این مسئله هم نبود. جرلامو مینویسد:
”از اوایل
جوانی، من برای فراگیری شمشیربازی تلاش فراوانی کردم، تا آنکه بواسطه تمرینات
مداوم توانستم حتی در میان استادان این فن نیز جایگاهی کسب کنم ... هنگام شب،
برخلاف لباس اشرافی که بتن داشتم، خود را مسلح میکردم و در اطراف شهرهایی که در
آنها منزل گزیده بودم پرسه میزدم ... روپوشی از ابریشم سیاه بتن میکردم تا ظاهرم
را بپوشاند، و کفشهایی از پشم گوسفند بپا میکردم ... اغلب در طول شب سرگردان بودم
تا صبح سر برسد.“
این گفتهها
تفکر برانگیز است.
کاردانو
که در سال 1525 مدرک پزشکی خود را دریافت نمود، تلاش کرد تا به مدرسه عالی پزشکان
میلان وارد شود، ولی پذیرفته نشد. دلیل رسمی اینکار ظاهراً حرامزادگی وی بود، اما
در حقیقت دلیل اصلی بینزاکتی و بیپروایی او بود که زبانزد همه بود. بنابراین
بجای اینکه به این مدرسهعالی پراعتبار بپیوندد، برای خودش در دهکده ساکو یک مطب
باز کرد. اینکار برای او عایدی مختصری میآورد، ولی کار او خیلی لنگ بود. جرلامو
با لوسیا باندارینی[67]، دختر یک افسر دریایی ازدواج کرد و به امید
اینکه برای خانواده خود درآمد بیشتری کسب کند به نزدیکی میلان نقل مکان کرد. ولی
بازهم مدرسهعالی او را نپذیرفت. وی که از داشتن یک شغل پزشکی قانونی ناامید شده
بود دوباره به قمار روی آورد. ولی حتی مهارتهای ریاضی او هم نمیتوانست ثروت
برباد رفته او را احیاء کند.
هنگامی که
تمامی اثاث خانه و جواهرات لوسیا را گرو گذاشتند، سرانجام کل خانواده در یک خانه
محقر منزل گزیدند. در همین زمان فرزند اول آنها هم بدنیا آمد. او مینویسد:
”بعد از
اینکه همسرم دوبار سقط جنین کرد و دو پسر نارس چهار ماهه را انداخت، گاه گاهی
احساس شومی به من دست میداد ... همسرم اولین فرزندمان را که پسر بود زایید ...
گوش سمت راستش کر بود ... دو انگشت پای چپش بهم چسبیده بودند. پشتش کمی کج بود،
ولی نه آنقدر که ناقصالخلقه باشد. پسرم تا سن بیست و سه سالگی زندگی آرامی را
گذراند. پس از آن عاشق شد ... و با زنی بدون جهیزیه، بنام بِرَندونیا دی سرونی،
ازدواج کرد.“
در این
زمان پدر مرحومش، بصورتی غیر مستقیم به یاری آنها آمد. سمت استادی فازیو در
دانشگاه هنوز خالی بود و جرلامو این منصب را بدست آورد. او باوجود اینکه گواهینامه
رسمی نداشت، کمی هم طبابت میکرد. تعدادی از بیماران وی که بصورت معجزهآسائی شفا
پیدا کرده بودند (شاید از روی شانس، و شاید از بابت پیشرفت پزشکی در آن دوره) موجب
اعتبار بسیاری برای او شد. حتی برخی از اعضای مدرسه عالی نیز مشکلات پزشکی خود را
نزد وی مطرح میکردند، و برای مدتی بنظر میرسید که شاید این راهگشای ورود او به
این موسسه معروف شود. ولی یکبار دیگر رکگوئی جرلامو همه چیز را برباد داد؛ او در
مقالات تندی، آبرو و اعتبار اعضای مدرسهعالی را زیر سئوال برد. جرلامو بر بینزاکتی
خود آگاه بود ولی ظاهراً آنرا بعنوان یک عیب قلمداد نمیکرد: ” بعنوان یک مدرس و
مناظره کننده، من خیلی جدیتر و دقیقتر بودم تا اینکه بخواهم جانب احتیاط را رعایت
کنم.“ در سال 1537 عدم نزاکت وی باعث شد تا آخرین مقالاتش رد شود.
ولی شهرت
وی بقدری زیاد بود که نهایتاً مدرسه عالی هیچ چارهای جز قبول او نداشت و او دو
سال بعد به عضویت پذیرفته شد. اوضاع رو به خوبی بود؛ از آن بهتر وقتی بود که دو
کتاب او درمورد ریاضیات منتشر شد. زندگی حرفهای وی در چند جبهه به پیش میرفت.
در همین
اثناء، تارتالیا یک کشف عمده کرد و راه حلی برای طیف وسیعی از معادلات درجه سوم
بدست آورد. بعد از اطمینان دادنهای کاردانو و بیمیلی تارتالیا در افشاء راز
بزرگش، نهایتاً او رازی شد تا راه حل خود را برای کاردانو بگوید. هنگامی که شش سال
بعد نسخهای از کتاب ”هنر عظمی“ بدست تارتالیا رسید و متوجه شد که رازش
بصورت آشکاری افشاء شده، دور از انتظار نبود که خشمگین شود.
در واقع
کاردانو اعتبار اینکار را به نفع خود ندزدیده بود، زیرا بطور کامل در کتاب خود از
تارتالیا قدردانی میکند:
”در زمان
ما، اسکیپیونه دل فِرو[68] از اهالی بولونیا حالتی از معادله درجه سوم
که بصورت مکعب مجهول بهاضافه مجهول برابر با عدد ثابت است را حل کرده، که
برای خود دستاوردی بزرگ و ستودنی محسوب میشود ... در رقابت با او، دوست من نیکولا
تارتالیا اهل برشا همین مسئله را در رقابتی با شاگرد دل فرو، آنتونیو ماریا فیور
حل کرد و موجب شد تا من از عهدی که با او بستم خلاص شوم.“
بااینحال
برای تارتالیا آزار دهنده بود که میدید راز گرانقدر او بر همه آشکار شده، از آن
آزار دهندهتر این بود که میدید بسیاری از خوانندگان کتاب بیش از اینکه کاشف
حقیقی مسئله را تحسین کنند، نویسنده کتاب را بخاطر میآورند.
حکایتی که
بیان شد نظر تارتالیا نسبت مسئله بود، و تقریباً بیشتر مدارک موجود در این زمینه
را تشکیل میداد. همانطور که ریچارد ویتمر در ترجمه کتاب ”هنر عظمی“ اشاره
میکند، ”اتکای ما درباره این موضوع بیشتر بر مطالبی است که تارتالیا منتشر کرده،
و به تمام معنا جنبه اعتراضی دارند.“ بعدها یکی از پیشخدمتهای کاردانو بنام لودو
ویکو فِرّاری[69] ادعا کرد که در جلسه ملاقات این دو حضور داشته و هیچ صحبتی در
مورد اینکه راهحل مخفی نگاه داشته شود درکار نبوده. بعدها فراری شاگرد کاردانو
شد، و معادلات درجه چهارم را حل کرد (یا در حل آنها سهیم بود). بنابراین نمیتوان
او را شاهدی عینیتر از تارتالیا محسوب کرد.
چیزی که
اوضاع را برای تارتالیای بیچاره بدتر میکرد تنها اعتبار از دست رفته نبود. در
اروپای دوره رنسانس، اسرار ریاضی میتوانست به پول نقد تبدیل شود، نه فقط از راهی
که کاردانو در قمار درپیش گرفت، بلکه از راه مسابقات عمومی.
اغلب گفته
میشود که ریاضیات ورزشی نیست که بیننده زیادی داشته باشد، ولی این مورد در سالهای
1500 میلادی صحت نداشت. ریاضیدانان با به چالش طلبیدن یکدیگر در مسابقات عمومی، و
طرح یک سری از مسائل برای حریف، از زندگی قابل قبولی برخوردار بودند. کسی که
بیشترین جوابهای صحیح را بدست میداد برنده مسابقه بود. این مسابقات به هیجانانگیزی
مشتبازی یا شمشیربازی نبود، ولی تماشاچیان، حتی اگر مسئلهای که مطرح میشده، و
یا راه حلی که شرکت کننده ارائه میداد را نمینفهمیدند، میتوانستند روی شرکتکننده
مورد نظر شرطبندی کنند و ببینند کدام یک از آنها برنده میشوند. علاوه بر پولی که
داده میشد، برنده میتوانست شاگردانی را به خود جذب کند تا برای آموزش از آنها
پول دریافت کنند.

تارتالیا
اولین کسی نبود که برای حل معادلات درجه سوم روشی جبری یافته بود. در حوالی سال
1515 اسکیپیونه دل فِرو، استاد اهل بولونیا، برای برخی از معادلات درجه سوم
روشهای مشابهی یافته بود. او در سال 1526 فوت کرد و هم نوشتههایش و هم کرسی
استادیش به دامادش آنیباله دل ناوه[70] رسید. ما میتوانیم از این موضوع مطمئن
باشیم، زیرا به لطف تلاشهای بارتولوتی[71]، این نوشتهها در سال 1970 در کتابخانه
دانشگاه بولونیا پیدا شد. بنابر اظهارات بارتولوتی، دل فرو احتمالاً میدانسته که
چگونه میتوان سه نوع مختلف از معادلات درجه سوم را حل کرد، ولی او تنها به حل یک
نوع از آنها اشاره کرده: مکعب مجهول بعلاوه مجهول برابر است با یک عدد معلوم.
این راه
حل توسط داماد دل فرو، دل ناوه، و شاگردش آنتونیو ماریو فیور، محفوظ نگاه داشته
شد. فیور که مصمم بود موقعیت خود را بعنوان یک معلم ریاضی تثبیت کند، از یک فن
موثر استفاده کرد. آن فن هم چیزی نبود جز دعوت به مبارزه. او در سال 1535 بصورت
عمومی تارتالیا را برای حل معادلات درجه سوم به چالش گرفت.
شایعاتی
مبنی بر اینکه روشهایی برای حل جبری معادلات درجه سوم یافت شده بر سر زبانها بود،
و هیچ چیزی برای یک ریاضیدان دلگرم کنندهتر از این نیست که بداند یک مسئله راه
حلی دارد. ریسک اتلاف وقت روی مسئلهای که قابل حل نیست، موجب میشد تا کسی
طرف آن نرود؛ خطر عمده آنجا بود که ممکن است شما آنقدر باهوش نباشید که به جوابی
برسید که میدانید وجود دارد. آنچه شما به آن نیاز دارید مقدار زیادی اعتماد بنفس
است، چیزی که ریاضیدانان بندرت فاقد آن هستند.
تارتالیا
روش دل فرو را دوباره کشف کرد، ولی به این مسئله ظن داشت که فیور راه حل انواع
دیگری از معادلات درجه سوم را نیز در دست دارد یا نه، مسئلهای که میتوانست موجب
برتری فیور نسبت به وی باشد. تارتالیا نقل میکند که این موضوع چقدر مایه نگرانی
او شده بود، و اینکه نهایتاً توانست تا کمی قبل از مسابقه، بقیه حالتهای مسئله را
حل کند. حالا تارتالیا در موقعیت برتر قرار داشت، و سریعاً فیور نگونبخت را از
دور خارج کرد.
داستان
این شکست همهجا پیچید؛ و این موضوع در میلان به گوش کاردانو هم رسید. در آن زمان
وی مشغول کار بر روی کتاب جبر خود بود. مانند هر مؤلف واقعی، کاردانو نیز مصمم بود
که آخرین کشفیات در حوزه جبر را در کتاب خودش شامل کند، چه اگر اینکار را نمیکرد
کتابش حتی قبل از اینکه منتشر شود یک اثر کهنه بحساب میآمد. پس کاردانو به امید
اینکه با تعریف و تشویف بتواند به راز تارتالیا پی ببرد و آن را در کتاب ”هنر
عظمی“ خودش بگنجاند به وی نزدیک شد. تارتالیا به بهانه اینکه خود او نیز قصد
دارد تا کتابی را منتشر کند از اینکار سرباز زد.
نهایتاً
اصرار و سماجت کاردانو جواب داد و تارتالیا راز خودش را برای وی افشاء کرد. آیا
تارتالیا با اینکه میدانسته کاردانو قصد دارد یک کتاب منتشر کند، واقعاً او را
قسم داده بود تا این راز را پنهان نگاه دارد؟ یا او تسلیم دلگرمیها و تشویقهای
کاردانو شده بود و البته بعد از این کار پشیمان شده؟
هیچ شکی
نیست که وقتی کتاب هنر عظمی منتشر شد تارتالیا بسیار خشمگین شد. یک سال بعد
خود او کتابی منتشر کرد بنام ”سئوالات و اختراعات گوناگون“، که در آن با
شدیدترین لحن به کاردانو تاخته بود. در این کتاب او به کلیه مکاتباتی که بین آن دو
بعمل آمده، و نیز متن کامل آنها، اشاره میکند.
در سال
1547 فراری برای دفاع از اربابش وارد صحنه شد و در مورد هر موضوعی که تارتالیا
بخواهد او را بچالش طلبید. او یک جایزه 200 سکهای برای برنده تعیین کرد و نظرش را
دراینمورد بصورت روشن بیان کرد: ”به این دلیل من این پیشنهادها را مطرح میکنم که
نشان دهم تهمتهایی که شما در مورد سینیور جرلامو روا داشتهاید در مقایسه با
شخصیت شما هیچ ارزشی ندارند.“
فراری متن
چالش خواهانه خود را به تعداد زیادی از دانشمندان و افراد سرشناس ارسال کرد. ظرف
مدت نه روز تارتالیا به استناد به حقایق مورد نظر خودش به این نامه پاسخ داد و دو
ریاضیدان در طول مدت یک سال ونیم، روی هم رفته دوازده مسئله را بین خود رد و بدل
کردند. این بحث و مجادله درست از قواعد دوئل پیروی میکرد. تارتالیا که از طرف
فراری به چالش کشیده شده بود اجازه یافت که سلاح مورد نظرش را، که در اینجا موضوع
بحث بود، انتخاب کند. ولی او مرتباً درخواست میکرد بجای فراری با کاردانو مباحثه
کند.
بلاخره
فراری بر خشم خود فایق آمد و براین مطلب تکیه کرد که آن کسی که اول از همه معادلات
درجه سوم را حل کرده دل فرو بوده نه تارتالیا. از آنجا که دل فرو هیچ اعتراضی در
این مورد نکرده بود، چرا تارتالیا باید چنین رفتاری را از خود نشان دهد؟ این نکته
خوبی بود، و ممکن است تارتالیا متوجه آن شده باشد، زیرا قصد داشت از مسابقه
کنار برود. ولی او چنین کاری را نکرد، و دلیل آن میتواند شهر موطن او برشا باشد.
تارتالیا بدنبال سمت استادی در آن شهر بود و ممکن بود مقامات عالی آن شهر منتظر
بودند تا ببینند نتیجه آن مسابقه چه میشود.
در هر
صورت تارتالیا پذیرفت تا مباحثه انجام پذیرد و نهایتاً اینکار در اگوست 1548 در
مقابل جمع کثیری از مردم و در کلیسای میلان انجام گرفت. هیچ سابقهای از این اتفاق
ثبت نشده، جز اینکه تارتالیا در نوشتههای خود اشاره میکند که با نزدیکی به اوقات
شام مباحثه متوقف شد. این نشان میدهد که ممکن است مباحثه خیلی هم طولانی نبوده
است. گرچه بنظر میرسد فراری به آسانی برنده شده، زیرا پس از این واقعه پستهای
مهمی به او پیشنهاد شده، که نهایتاً منصب ارزیاب مالیاتی فرماندار میلان را قبول
کرده و به ثروت زیادی هم رسیده. از سوی دیگر تارتالیا هچ موقع ادعای پیروزی نکرد،
هیچ کرسی استادی را در برشا نگرفت و همیشه هم به تلخی درگیر رد و بدل اتهامات
متقابل بود.
در مقابل
آنچه بر تارتالیا پوشیده بود، کاردانو و فراری یک خط دفاعی کاملاً متفاوت در دست
داشتند، زیرا این دو به بولونیا سفر کرده، و دست نوشتههای دل ریو را از نزدیک
مورد بررسی قرار داده بودند. این نوشتهها شامل اولین راه برای حل جبری معادلات
درجه سوم بود، و سال بعد هر دو ادعا کردند که منبع اصلی آنچه در کتاب هنر عظمی آمده
این دست نوشتهها بوده نه آنچه تارتالیا برای کاردانو افشاء کرده، و ارجاعی که در
این کتاب به نام تارتالیا شده فقط از این لحاظ بوده که نشان دهد خود کاردانو چگونه
از کار دل فرو مطلع شده بود.
یک جنبه
دیگر این داستان نیز اهمیت پیدا کرد. اندکی پس از اینکه چاپ دوم کتاب هنر عظمی
منتشر شد، در سال 1570 کاردانو توسط دادگاههای تفتیش عقاید دستگیر و زندانی شد.
دلیل اینکار آنگونه که قبلاً تصور میشد محتوای کتاب نبود، بلکه موضوع بر سر کسی
بود که این کتاب به او اهداء میشد. کاردانو تصمیم گرفته بود این کتاب را به شخص
کمتر شناخته شدهای بنام آندریاس اوسیاندر اهداء کند. اوسیاندر شخصیت کماهمیتی در
جنبش اصلاحی آن زمان ایتالیا محسوب میشد. ولی از طرفی هم شدیداً به او ظن داشتند
که وی همان شخصی است که با اسم ناشناس بر کتاب معروف کپرنیک مقدمهای نوشته است.
کتاب کپرنیک یعنی ”درباره گردش اجرام آسمانی“، بجای زمین خورشید را مرکز
عالم میدانست، و کلیسا این کتاب را آنقدر کفرآمیز میدانست که در سال 1600
جیردانو برونو را بخاطر داشتن این کتاب زنده در آتش سوزاند. همین مسئله در سالهای
1616 و 1633 دو بار برای گالیله دردسر ساز شد، ولی اینبار دادگاه تفتیش عقاعد به
حبس خانگی او بسنده کرد.

بمنظور اینکه به ارزش دستآوردهای کاردانو و رقبایش
پی ببریم، ما باید ابتدا به لوحهای بابلی که چگونگی حل معادلات درجه دوم را بیان
میکرد نگاهی دوباره بیاندازیم. اگر بخواهیم دستورالعمل آنها را به شیوه نوین و با
استفاده از علائم بیان کنیم، در عمل آنچه خواهیم دید اینست که آنها میگفتند حل
معادله ax=b-x2 بصورت زیر خواهد بود:

این معادل
همان فرمولی است که هر دانشآموز دبیرستانی حفظ است، و امروزه در هر کتاب درسی
یافت میشود.
فرمول حل معادلات درجه سوم در دوره رنسانس نیز مانند
قبل، ولی مقداری پیچیدهتر است. اگر باز هم بخواهیم این فرمول را بصورت امروزی
نشان دهیم، باید بگوییم حل معادله درجه سوم x3+ax=b بصورت زیر خواهد بود:

تا آنجایی
که به خود فرمول مربوط میشود باید بگویم عبارت بالا فرمول سادهای حساب میشود
(باور کنید!)، ولی قبل از اینکه به توضیح آن بپردازیم شما باید کمی از مهارتهای
جبری برخوردار باشید. این پیچیدهترین فرمولی است که ما در این کتاب میبینیم، و
شامل هر سه علامتی است که قبلاً به آن اشاره کردم: یعنی حروف(مثل x)، توان، و علامت √ برای ریشه دوم و سوم.
نیازی نیست تا شما این فرمول را درک کنید، و مطمعناً نیازی نیست تا آنرا محاسبه
کنید. ولی شما باید شکل کلی آنرا درک کنید. قبل از هر چیز چند اصطلاح را برای شما
تشریح میکنم که برای ادامه راه مفید خواهند بود.
یک عبارت
جبری نظیر 2x4-7x3-4x2+9
یک چندجملهای نامیده میشود. چنین عباراتی با جمع کردن توانهای مختلف
مجهول با یکدیگر بدست میآیند. اعداد 2, -7, -4 , 9
که در توانهای مختلف ضرب میشوند، ضریب نامیده میشوند. بالاترین توان
موجود در یک چند جملهای درجه آن نامیده میشود. بنابراین چندجملهای ما
درجه 4 خواهد بود. جوابهای یک معادله که از روی یک چند جملهای ساخته شود (مثل0
= 2x4-7x3-4x2+9)
ریشههای آن چندجملهای نامیده میشوند.
حالا ما
به تشریح فرمول کاردانو میپردازیم. این فرمول متشکل از ضرایب a,b و ترکیبی از جمع،
تفریق، ضرب و تقسیم است (که فقط روی اعداد خاصی مثل 2, 4 , 27
انجام میگیرد.) چیز دشواری که دراینجا دیده میشود دو چیز است: یکی علامت ریشه دومی
است که در دو جا ظاهر میشود، در یک طرف جمع و در طرف دیگر تفریق میشود. و
نهایتاً دو علامت ریشه سوم هستند، که در زیر آنها عباراتی قرار گرفته که شامل ریشه
دوم است. همه آنچه نیاز داریم همین است، و فکر نمیکنم با کمتر از این بتوانم
کارمان را جلو ببریم.
آنچه
ابتدا ریاضیدانان دوره رنسانس نتوانستند آنرا درک کنند، ولی بزودی نسلهای آتی به
آن پی بردند، این بود که این فرمول تنها برای یک نوع خاص از معادلات درجه سوم
کاربرد نداشت. اگر معادلات را کمی دستکاری کنیم، این فرمول برای حل همه
انواع معادلات درجه سوم کاربرد دارد. برای شروع، مثلاً اگر جمله توان سوم ما بجای x3 بصورت 5x3
باشد، شما میتوانید کل معادله را بر 5 تقسیم کنید تا ضریب 5
از 5x3 حذف شود (که البته ریاضیدانان
دوره رنسانس مطمئنناً آنقدر باهوش بودند که آنرا درک کنند). یک جنبه ظریفتر، که
به انقلابی از تصورات ما نسبت به اعداد نیاز داشت، این بود که ضرایب a, b بتوانند در صورت لزوم اعداد
منفی باشند. و بالاخره این موضوع که اگر معادله دارای جمله درجه دوم است شما
همیشه میتوانید (با استفاده از ترفندهای جبری) از شر آن جمله خلاص شوید. اینکار به
اینصورت انجام میگیرد که x را با حاصل جمع x
و یک عدد بادقت انتخاب شده جایگزین کنید، و اگر اینکار را بدرستی انجام
دهید همشه جمله درجه دوم حذف میشود. بار دیگر تکرار میکنم که نگران این نباشید
که اعداد مثبت هستند یا منفی. ریاضیدانان رونسانس نگران جملههای بودند که از
معادله غایب بودند، ولی از دید ریاضیات نوین چاره این کار بسیار ساده است: در
حقیقت هیچ جملهای در معادله غایب نیست، بلکه این تنها ضریب آنها است که
صفر میباشد و برای حل چنین معادلاتی نیز تنها به یک فرمول نیاز است.

آیا مسئله
حل شد؟
نه
کاملاً، من دروغ گفتم.
اینجا
دلیل دروغ گفتنم را شرح میدهم. من گفتم که فرمول کاردانو همه نوع معادله درجه
سوم را حل میکند. دلیلی هست که نشان میدهد میدهد این مورد دقیقاً صحیح نیست، و
معلوم شده که این موضوع اهمیت دارد. گرچه دروغی را که من بشما گفتهام، دروغ خیلی
بدی بحساب نمیآید، زیرا به این بستگی دارد که منظور شما از ”حل“ یک معادله چه
باشد.
کاردانو
خودش متوجه این مشکل شده بود، معادلات درجه سوم نوعاً یا دارای سه ریشه (جواب)
هستند، یا اصلاً جواب ندارند. کاردانو متوجه شد که وقتی برای معادله سه ریشه وجود
داشته باشد (مثلاً 1،2،3) بنظر نمیرسد فرمول جواب با معنایی بدهد. در عوض
اعدادی که زیر ریشه دوم قرار میگیرند اعداد منفی میشوند.
بویژه کاردانو متوجه شد که معادله x3
= 15x + 4 بطور وضوح داری جواب x=4 است. ولی وقتی او سعی کرد فرمول تارتالیا را برای این
معادله بکار بگیرد به ”جواب“ زیر میرسید:
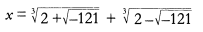
که بنظر
بیمعنی میآمد.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
کدام
راه را طی میکرد؟ کدام رشته را برمیگزید؟ او هر دو آنها را دوست داشت، ولی باید
میان آنها یکی را انتخاب میکرد. وضعیت دشواری بود. سال 1796 بود و یک جوان
بااستعداد 19 ساله با تصمیمی روبرو بود که بر باقی عمر او تاثیر میگذاشت. او باید
شغل آینده خود را انتخاب میکرد. گرچه از یک خانواده معمولی آمده بود، ولی کارل
فردریش گاوس[74] میدانست که میتواند به اوج ترقی برسد. همه از تواناییهای او
آگاه بودند، از جمله دوک برونزویک[75]، که گاوس در قلمرو او بدنیا آمده بود و
خانواده وی در آنجا زندگی میکردند. مشکل او این بود که قابلیتهای فراوانی داشت و
مجبور بود از میان دو عشق عمده خود، یعنی ریاضیات و زبانشناسی، یکی را برگزیند.
ولی در 30
مارس، با کشف غیرمنتظره و خارقالعادهای که او انجام داد، تصمیم گرفته شد، تصمیمی
که از دست وی خارج بود. در آن روز گاوس روشی را کشف کرد که با استفاده از خطکش و
پرگار میتوانست یک هفدهضلعی منظم بسازد.
ممکن است
مبهم بنظر برسد، ولی این موضوعی نبود که حتی اقلیدس هم اشارهای به آن داشته باشد.
شما میتوانید روشهایی برای ساختن چندضلعیهای منظمی با 3، 4، 5 و یا 6 ضلع پیدا
کنید. با ترکیب روش ساخت 5ضلعی و 3ضلعی، شما میتوانید 15ضلعی بسازید، و به همین
ترتیب با ترکیب روشهای دیگر میتوانید 8، 10، 12، 16 و 20 ... ضلعی بسازید.
ولی ساخت
17ضلعی چیز دیوانه کنندهای بود. این یک واقعیت بود، و گاوس بخوبی دلیل آنرا میدانست.
دلیل اصلی این امر بر دو خاصیت ساده عدد 17 استوار بود. یکی اینکه 17 یک عدد اول
است (یعنی غیر از خودش و یک بر هیچ عدد دیگری بخشپذیر نیست) و دوم اینکه تفاوت 17
و شانزده، که توانی از 2 است تنها برابر 1 است:
17 = 16 + 1
= 24 + 1.
اگر شما
نیز مانند گاوس یک نابغه بودید، آنگاه میتوانستید ببینید که چرا خاصیتهای فوق بر
وجود یک ساخت اقلیدسی (ساخت با خطکش و پرگار) برای یک هفدهضلعی منظم دلالت دارد.
ولی اگر شما جزء ریاضیدانانی بودید که از سال 500 ق.م تا سال 1796 میزیستهاند،
آنگاه شما کوچکترین ربطی نسبت به این موضوع نمیدیدید. ما حالا میدانیم که چرا
کسی در این مدت به این رابطه پی نبرده بود.
اگر گاوس
چیزی نیاز داشت تا استعداد او را در ریاضی تائید کند، قطعاً حالا به آن دست یافته
بود. او تصمیم گرفت یک ریاضیدان شود.

خانواده
گاوس در سال 1740 هنگامیکه پدر بزرگش بعنوان یک باغبان در برونزویک مشغول بکار شد
به آنجا نقل مکان کردند. یکی از سه پسر او بنام گبهارد دیتریش نیز باغبان شد. وی
معمولاً بکارهای دیگری مثل آجرچینی و کانال کشی نیز مشغول بود؛ در برخی اوقات نیز
به کارهای نظیر فواره سازی، دستیار تاجر، و صندوقداری یک موسسه بیمه کوچک میپرداخت.
کارهای پردرآمدتر معمولاً در دست اصناف بود و تازه واردها (حتی تازهواردهای نسل
دومی) به آن دسترسی نداشتند. گبهارد در سال 1776 با همسر دومش بنام دوروتیآ بنز،
که دختر یک سنگتراش بود و بعنوان یک پیشخدمت مشغول بکار بود، ازدواج کرد. فرزند
پسر آنها کارل فردریش در سال 1777 بدنیا آمد.
گبهارد
مردی درستکار ولی کله شق، بدخو، و البته نهچندان باهوش بود. دوروتیا باهوش و
اعتماد بنفس داشت، خصوصیاتی که بعداً کارل آنها را از وی به ارث برد. هنگامی که
پسرش تنها دو سال داشت او میدانست که فرزندش یک نابغه است. از طرف دیگر، او مصصم
بود که کارل از چنان تحصیلاتی برخوردار شود که استعدادهای او را شکوفا کند. پدرش
خوشحالتر میشد اگر میدید که پسرش هم مانند او یک آجرچین شده. ولی کارل به نعمت
مادرش، به چنان درجهای از کمال رسید که کلیه پیشگوییهای که درمورد او بعمل آمده
بود به حقیقت پیوست، از جمله پیشگوی که هندسهدان معروف ولفگانگ بویویی[76] که برای مادش گفته بود که روزی کارل ”بزرگترین ریاضدان اروپا“ میشود.
دوروتیا چنان از شنیدن این حرف خوشحال شد که به گریه افتاد.
پسر به از
خودگذشتگی مادر پاسخ گفت، و در بیست سال آخر عمر مادرش، در خانه پیش او زندگی کرد.
در آن هنگام چشمهای مادرش کمسو شده بود تا اینکه نهایتاً کور شد. ریاضیدان برجسته
اصرار داشت که خودش از او پرستاری کند و اینکار را تا هنگام مرگ وی در سال 1839
انجام داد.
گاوس از
اوان کوکی نبوغ خود را نشان داد. روزی پدرش مشغول توزیع حقوق میان کارگران بود، و
او که در آن موقع تنها سه سال داشت متوجه یک اشتباه محاسبه شد، و آن را به گبهارد
که مبهوت شده بود گوشزد کرد. هیچ کسی تا آن موقع اعداد را به او یاد نداده بود،
این خودش بود که اینکار را آموخته بود.
چند سال
بعد معلم مدرسه ابتدایی گاوس، که گ. گوتتر نام داشت، برای اینکه شاگردان کلاسش را
چندساعتی مشغول نگاه دارد و استراحتی کند، از آنها خواست که اعداد 1 تا 100 را با
هم جمع کنند. به این نوع مسائل تصاعد حسابی میگویند و برای محاسبه آن قاعده سادهای
وجود دارد، ولی این چیزی نبود که دانشآموزان این کلاس از آن اطلاعی داشته باشند،
بنابراین تنها راه حل این بود که این اعداد را یکی یکی با هم جمع کنند.
حداقل این
چیزی بود که معلم آنها انتظار داشت. او به شاگردانش گفت وقتی تکلیف خود را انجام
دادند، جواب مسئله را روی لوح خود بنویسند و آن روی میز او بگذارند. در حالی که
همشاگردیهایش به روشی مانند زیر اینکار را انجام میدادند:
3=1+2
6=3+3
10=4+6
و در این
میان اشتباهاتی نظیر زیر هم اجتناب ناپذیر بود
14=5+10
با اینحال
گاوس برای لحظهای فکر کرد، با گچ عددی را روی لوحش نوشت سپس بلند شد و لوح را روی
میز معلم گذاشت.
در پایان
کلاس هنگامی که معلم تمام لوحها را جمعآوری کرد، تنها یک نفر جواب درست را نوشته
بود و آنهم کسی نبود جز گاوس.
ما
نمیدانیم که چگونه راه حل این مسئله به ذهن گاوس رسید، ولی میتوانیم تا حدود
زیادی آنرا پیشبینی کنیم. به احتمال زیاد گاووی قبلاً به چنین جمعی فکر کرده بود و
یک ترفند عملی برای آن یافته بود. ( اگر هم چنین نبود، او از چنان استعدادی
برخوردار بود که میتوانست اینکار را فیالبداهه انجام داده باشد). یک راه حل ساده
برای اینکار دسته بندی سلسله اعدادی است که باید با هم جمع شوند: 1 با 100، 2 با
99، 3 با 98 و به همین ترتیب تا برسیم به 50 با 51. هر عدد از 1 تا 100 تنها یکبار
در یکی از این دسته بندیها ظاهر میشود، بنابراین حاصل جمع این دستهها با حاصل
جمع مطلوب ما یکی است. ولی بسادگی میتوان دید که مجموع هر کدام از این دستهها 101
میشود، و چون 50 دسته داریم حاصل جمع آنها روی هم میشود 5050 = 101×50
. این راه حل (و یا چیزی شبیه به این) بود که با استفاده از آن گاوس توانست سریعاً
جواب را روی لوح بنویسد.
نکتهای
که در این حکایت هست بر این دلالت نمیکند که گاوس قادر نبود بسرعت محاسبات را
انجام دهد. کارهای نجومی که وی بعدها انجام داد شامل محاسبات فراوانی بود که وی با
دقتی زیاد، و با سرعتی همچون یک دانشمند دیوانه انجام میداد. ولی سادهتر کردن
محاسبات یکی از هنرهای او بود. آنچه که وی به وفور از آن برخوردار بود، استعدادی
بود که در یافتن الگوهای پنهان در مسائل مختلف ریاضی داشت.
معلم او،
بوتتنر، از این عمل گاوس چنان متحیر شد که بهترین کتاب حسابی را که تا آن زمان
موجود بود به او داد. ظرف مدت یک هفته گاوس تمام مطالبی را که معلمش در چنته داشت
فرا گرفت.
تصادفاً
بوتتنر یک دستیار 17 ساله بنام یوهان بارتل داشت که وظیفه اصلی او تیز کردن قلم
برای نوشتن و همچنین کمک به دیگر شاگردان بود. بارتل نیز به ریاضیات علاقه داشت.
او مجذوب گاوس 10 ساله شد، و در میان این دو، رفاقتی قوت گرفت که تا آخر عمر ادامه
داشت. آنها با یکدیگر ریاضی کار میکردند، و هر یک دیگری را به اینکار تشویق میکرد.
بارتل با
برخی از افراد سرشناس برونزویک آشنا بود، و این موجب شد تا این افراد سرشناس بزودی
مطلع شوند که در نزدیکیشان نابغه ناشناختهای هست که خانواده او در تنگدستی زندگی
میکنند. یکی از این نجیبزادگان بنام آ. زیمرمان درسال 1791 گاوس را به به دوک
برونزویک، کارل ویلهلم فردیناند، معرفی کرد. دوک که شیفته گاوس شده بود، همانگونه
که در مورد دیگر کودکان فقیر و بااستعداد عمل میکرد، مخارج تحصیل او هم را بر
عهده گرفت.
ریاضیات
تنها استعداد این پسر نبود. او هنگامی که به 15 سالگی رسید بقدری در زبانهای
کلاسیک مهارت یافت که دوک تصمیم گرفت تا وی در دبیرستان به زبان آموزی مشغول شود.
این مسئله باعث شد تا بعدها بسیاری از کارهای برجسته او به زبان لاتین نوشته شود.
وقتی بسن 17 سالگی رسید، او یکی از شگفت انگیزترین قوانین نظریه اعداد، که ”قانون
تقابل مربعی[77]“ نامیده میشود، را کشف کرد. این قانون درباره خاصیت عجیب ولی
منظم بخشپذیری است که در میان مربعهای کامل وجود دارد. این الگو قبلاً توسط
لئونارد اویلر[78] تشخیص داده شده بود، ولی گاوس که کاملاً از این قضیه بیخبر بود
خودش دوباره آنرا کشف کرد. تعداد اندکی از مردم بودند که در مورد اساس معادلات فکر
کنند، ولی گاوس جوان درباره نظریه معادلات بصورتی عمیق اندیشه میکرد. در حقیقت
همین فکر بود تا باعث شد وی بتواند مسئله ساختن 17-ضلعی منظم توسط خطکش و پرگار
را حل کند و راهی باشد برای جاودانگی او در دنیای ریاضیات.

ما بین
سالهای 1795 تا 1798 گاوس مشغول تحصیل در دانشگاه گوتینگن بود و بار دیگر هزینه
تحصیلش را فردیناند پرداخت میکرد. او دوستان کمی داشت، ولی وقتی هم با کسی دوست میشد
این دوستی چنان پایدار بود که تا آخر عمر دوام میآورد. در دانشگاه گوتینگن بود که
گاوس با با هندسهدان برجسته، و وفادار به سنتهای اقلیدسی، وُلفگانگ پولیای آشنا
شد.
ایدههای
ریاضی چنان بسرعت به سراغ گاوس میآمدند که برخی اوقات بنظر میرسید که او کاملاً
در آنها غرق شده. هنگامی که چنین افکاری به او هجوم میآورد، ناگهان هرکاری که
داشت متوقف میکرد و به دوردستها خیره میشد. در طی همین تفکرات درونی بود که او
به درستی هندسه اقلیدسی شک کرد. آنچه بیش از همه فکر وی را مشغول میکرد، کتابی
بود که در دست نوشتن داشت. این کتاب تحقیقات حسابی[79]
نام داشت و بیشتر آن تا سال 1798 تکمیل شده بود. ولی گاوس میخواست مطمئن شود که
اگر مطالبی در این کتاب هست که مربوط به پیشینیان اوست، اعتبار آن هم نصیب آنها
شود. بنابراین به دانشگاه هِلماشتت رفت که کتابخانه آن در آلمان از غنیترین
منابع برای ریاضیات برخوردار بود و توسط سرشناسترین ریاضیدان آلمان یعنی یوهان
پفاف[80] اداره میشد.
پس از
تاخیر زیادی که در چاپخانه پیش آمد، بالاخره کتاب تحقیقات حسابی در
سال 1801 منتشر شد. کتاب سبکی سازشناپذیری داشت؛ قضایا به شکلی منطقی و بادقت
اثبات شده بودند، ولی سبک نوشتن این کتاب به هیچ وجه خواننده را به بصیرتی که در
پس این قضایا بود راهنمایی نمیکرد. پس از این هم وی همین سبک نوشتن را ادامه داد
و در توجیه آن میگفت ”وقتی کسی عمارت زیبایی را بنا میکند، چهارچوبهای آن پس از
اتمام ساخت نباید پیدا باشد“. البته این حرف بشرطی درست است که فقط زیبایی بنا، و
تحسین از آن اهمیت داشته باشد. اگر شما بخواهید به دیگران طریقه بنا شد ساختمان را
آموزش دهید، این این روش نمیتواند خیلی مفید باشد. کارل گوستاو ژاکوب ژاکوبی[81]، که کارهای او درباره آنالیز اعداد مختلط بر اساس ایدههای گاوس
بنا شده، درباره این ریاضیدان نامی قبل از خود چنین میگوید: ”او همچون روباه مکاری
میماند، که وقتی روی شن راه میرود، با دمش رد پایش را پاک میکند.“

در همین
ایام بود که ریاضیدانان بتدریج متوجه شدند که گرچه اعداد ”مختلط“ بنظر مصنوعی میآمدند،
و معنای آنها نیز غیر قابلفهم بود، ولی آنها با فراهم آوردن یکنواخت جواب برای
معادلات موجب میشدند تا جبر مرتبتر و آراستهتر از قبل شود. ظرافت و سادگی معیار
اصلی ریاضیات است، و اگر ایدههای نوین کمک کنند تا این سادگی و ظرافت حفظ شود،
نهایتاً پیروز میدان خواهند بود، حال هر چند هم که در ابتدا عجیب بنظر برسند مهم
نیست.
اگر شما
تنها با اعداد سنتی که ”اعداد حقیقی“ نامیده میشود کار کنید، حل معادلات بصورت
پردردسری نامرتب میشوند. مثلاًً معادله x2-2=0
دارای دو جواب مثبت  و
و
 -
است، ولی معادلهای که خیلی به معادله قبلی شباهت دارد، مثل x2+1=0،
اصلاً دارای جوابی نیست. بااینحال این معادله در قلمرو اعداد مختلط دارای دو جواب
i و -
i است. در اینجا i جایگزینی برای
-
است، ولی معادلهای که خیلی به معادله قبلی شباهت دارد، مثل x2+1=0،
اصلاً دارای جوابی نیست. بااینحال این معادله در قلمرو اعداد مختلط دارای دو جواب
i و -
i است. در اینجا i جایگزینی برای 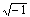 است
که در سال 1777 توسط اویلر ابداع شد، ولی تا سال 1794 بصورت گسترده از آن استفاده
نشد. اگر نظریه معادلات تنها به اعداد ”حقیقی“ تکیه کند، پیچیده و پر از استثنا
خواهد بود. درعوض نظریه مشابهای که بر پایه اعداد مختلط بنا شود، چون از ابتدا
خود را با یک عارضه بزرگ روبرو میکند، از تمام این عوارض جانبی اجتناب خواهد کرد:
این عارضه بزرگ این است که اجازه دهیم معادلات هم ریشه حقیقی، و هم ریشه مختلط
داشته باشند.
است
که در سال 1777 توسط اویلر ابداع شد، ولی تا سال 1794 بصورت گسترده از آن استفاده
نشد. اگر نظریه معادلات تنها به اعداد ”حقیقی“ تکیه کند، پیچیده و پر از استثنا
خواهد بود. درعوض نظریه مشابهای که بر پایه اعداد مختلط بنا شود، چون از ابتدا
خود را با یک عارضه بزرگ روبرو میکند، از تمام این عوارض جانبی اجتناب خواهد کرد:
این عارضه بزرگ این است که اجازه دهیم معادلات هم ریشه حقیقی، و هم ریشه مختلط
داشته باشند.
تا سال
1750 کلیه نظراتی که توسط ریاضیدانان دوره رنسانس در ایتالیا ارائه شده بود به
حدکمال رسیده و بسته شدند. روش حل آنها برای حل معادلات درجه سوم و چهارم امتداد
روشهای بابلیان برای حل معادلات درجه دوم بود. ارتباط میان رادیکالها و اعداد
مختلط بصورت گستردهای مورد مطالعه قرار گرفت، و معلوم شد که در گسترش دستگاه
اعداد معمولی به دستگاه اعداد مختلط، ریشه سوم یک عدد یکتا نیست، بلکه سه عدد
هستند که میتوانند ریشه سوم یک عدد باشند، یک عدد فقط دارای یک ریشه چهارم نیست،
بلکه 4 ریشه چهارم دارد، یک عدد فقط دارای یک ریشه پنجم نیست بلکه پنج ریشه پنجم دارد.
کلید فهم اینکه این ریشههای جدید از کجا آمدهاند از خاصیت زیبای ”ریشههای واحد“
ناشی میشود. ریشههای واحد یعنی ریشه nام عدد 1. این
ریشهها رئوس یک nضلعی منظم در صفحه مختلط را تشکیل میدهند
که یک راس آن در نقطه 1 قرار گرفته باشد.
بقیه ریشههای یک روی دایرهای به شعاع 1 و مرکز 0
بصورت مساوی پخش خواهند بود. برای مثال شکل سمت چپ نشاندهنده ریشههای پنجم عدد یک
است.
اگر بخواهیم بصورت عمومیتری بیان کنیم، باید گفت از
هر ریشه پنجم یک عدد مفروض، میتوان چهار ریشه دیگر آنرا با ضرب کردن آن در q, q2 , q3 , q4 بدست آورد. این اعداد نیز روی یک دایره به مرکز 0 بصورت مساوی پخش شدهاند.
برای نمونه ریشههای پنجم عدد 2 در شکل سمت راست نشان داده شده:
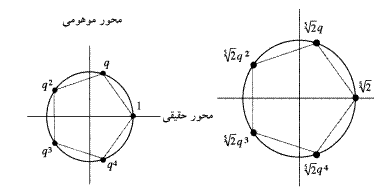
(چپ) ریشههای پنجم واحد در صفحه مختلط.
(راست) ریشههای پنجم عدد 2.
این مسئله
بسیار قشنگ بود، ولی به چیزی اساسیتری نیز اشاره میکرد. ریشه پنجم 2 را میتوان
بعنوان جواب معادله x5=2 درنظر گرفت. این معادله از درجه چنجم است، و پنج ریشه
مختلط دارد، که تنها یکی از آنها حقیقی است. بطور مشابه، معادله x4=2،
که جواب آن ریشههای چهارم عدد 2 هستند، دارای چهار ریشه است، معادله x17=2
دارای 17 ریشه است، و غیره... نیازی نیست که شما نابغه باشید تا به الگوی موجود پی
ببرید: تعداد ریشههای یک معادله برابر با درجه آن است.
بنظر میآید
این قاعده نه فقط برای ریشههای nام یک معادله ساده نظیر xn=2
کاربرد دارد، بلکه شامل هر معادله جبری از هرنوع آن میشود.
ریاضیدانان متقاعد شده بودند که در قلمرو اعداد مختلط، هر معادله به تعداد درجه
خود دارای جواب است. (البته این عبارت هنگامی درست است که ما ریشههای تکراری را
نیز بحساب بیاوریم، در غیر اینصورت باید گفت تعداد جوابهای یک معادله برابر درجه
آن، و یا کمتر از آن، است. اویلر این خاصیت معادلات را برای معادلات درجه 2 ، 3 و
4 ثابت کرد، و ادعا کرد که روشهای مشابهای برای درجات دیگر هم کار میکند. ایدههای
او قابل قبول بنظر میرسید، ولی معلوم شد پر کردن خلاء موجود با چنین روشهایی غیر
ممکن است، حتی امروزه هم تلاش زیادی لازم است تا با روش اویلر به نتیجه رسید. با
این وجود ریاضیدانان فرض را بر آن گذاشته بودند که اگر آنها یک معادله با درجه
مفروضی را حل میکردند، باید انتظار داشت که دقیقاً به تعداد آن درجه هم برای
معادله جواب پیدا کنند.
همانطور
که گاوس ایدههای خود را در زمینه نظریه اعداد و آنالیز بسط میداد، از اینکه میدید
هنوز کسی این فرض را ثابت نکرده بیشتر و بیشتر ناراضی بود. مشخصاً او به اثباتی
برای این قضیه دست یافت. این اثبات پیچیده و خیلی غیر مستقیم بود. هر ریاضیدان ذی
صلاحی میتوانست متقاعد شود که این برهان درست است، ولی هیچ کس نمیتوانست بفهمد
که چگونه گاوس در ابتدا متوجه آن شده بود. روباه ریاضیات کار خود را به حد احسنت
انجام داده بود.
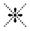
عنوان
پایان نامه دکترای گاوس به چیزی شبیه به این ترجمه میشود: ”یک اثبات جدید بر
اینکه هر تابع با درجه صحیح از یک متغیر میتواند به عوامل درجه یکم یا دوم حقیقی
تجزیه شود“. اگر بخواهیم این عبارت پرطمطراق قدیمی را به زبان امروزی بیان کنیم،
باید گفت که عنوان پایان نامه به این اشاره میکند که هر چندجملهای (با ضرایب
حقیقی) حاصل ضرب عباراتی است که یا خطیاند (درجه 1) و یا چندجملهای درجه دوماند.
گاوس
مخصوصاً از لغت ”حقیقی“ استفاده میکرد تا نشان دهد که او با دستگاه اعداد سنتی کار
میکند، دستگاهی که در آن اعداد منفی ریشه دوم ندارند. امروزه ما میگوییم که قضیه
گاوس بصورت منطقی معادل است با: ”هر چندجملهای حقیقی از درجه nام، دارای n جواب حقیقی ویا مختلط است.“ ولی گاوس عنوان مقاله خود را طوری برگزید که
کارش به دستگاه اعداد مختلط، که هنوز جا نیفتاده بود، متکی نباشد. با درنظر گرفتن
اینکه عوامل درجه یک (یا خطی) معادل ریشههای حقیقی هستند، ریشههای مختلط یک
چندجملهای حقیقی همیشه میتوانند طوری بصورت جفتی با هم ترکیب شوند که حاصل آنها
عوامل حقیقی درجه دوم شود. گاوس با استفاده از این دو لغت در عبارتبندی مقالهاش
(یعنی عوامل درجه یکم و دوم)، با زیرکی از موضوع بحثانگیز اعداد مختلط شانه خالی
کرد.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
پس
از انتشار کتاب ”هنر عظمی“ اثر کاردانو، عمدهترین پیشرفت در حل معادلات در
نیمه قرن هجدهم بوجود آمد. اگرچه ریاضیدانان دوره رنسانس میتوانستند معادلات درجه
سوم و چهارم را حل کنند، ولی روشهای آنها اساساً از یک سری ترفند تشکیل شده بود.
این ترفندها جواب میداد، ولی بیشتر بنظر میآمد که تابع تصادف هستند تا یک دلیل
اصولی. بلاخره در حدود سالهای 1770 دلیل این امر توسط دو ریاضیدان مشخص شد:
ژوزف-لویی لاگرانژ[95] که اصالتاً ایتالیایی بود ولی خود را
فرانسوی میدید، و الکساندر-تئوفیل واندرموند[96]، که قطعاً اهل فرانسه بود.
واندرموند
در سال 1735 در پاریس بدنیا آمد. پدرش میخواست او یک موسیقیدان شود، و هنگامی که
واندرموند در نواختن ویلن ماهر شد راه موسیقی را در پیش گرفت. ولی در سال 1770 به
ریاضیات علاقهمند شد. اولین مقالات ریاضی او در مورد توابع متقارن از ریشههای یک
چندجملهای بود (توابع متقارن فرمولهای جبری هستند که اگر جای ریشهها با یکدیگر
عوض شود، مقدار آنها تغییر نمیکند، مثلاً عبارتی مثل مجموع همه ریشهها.)
اصلیترین سهمی که او در ریاضیات داشت، اثبات این بود که معادله xn-1=0،
که با یک nضلعی متناظر است، را فقط درصورتی میتوان با
رادیکالها حل کرد که مقدار n
از 10 کمتر یا برابر آن باشد. (در واقع این معادله را میتوان
با هر مقداری برای n بوسیله رادیکالها حل کرد.) ریاضیدان بزرگ فرانسوی اگوستین کوشی بعدها نقل میکند
که واندرموند اولین کسی بوده که متوجه شده توابع متقارن میتوانند در حل معادلات
بوسیله رادیکالها بکار روند.
این ایده
برای لاگرانژ به سلاحی بدل گشت تا با استفاده از آن به تمام معادلات جبری یورش
ببرد.

لاگرانژ
در شهر تولین ایتالیا بدنیا آمد و نام اصلی او جوزپه لودُویکو لاگرانجیا[97] بود. خانوانده او وابستگیهای قوی به فرانسه داشتند. جد بزرگ او
قبل از اینکه به ایتالیا بیآید و به دوکِ ساووی خدمت کند، افسر سوارنظام
فرانسه بود. هنگامی که جوزپه جوان بود، نامخانوادگی لاگرانژ را برای خود انتخاب
کرد. پدرش خزانهدار شهرداری در تورین بود؛ مادرش، ترزا گروسو، دختر یک طبیب بود.
لاگرانژ اولین فرزند آنها از میان یازده نفر دیگر بود، که تنها دو نفر از آنها پس
از کودکی زنده مانداند.
گرچه
خانواده آنها از طبقه بالای جامعه اتالیا محسوب میشد، ولی به دلیل چند سرمایه
گذاری غلط، نقدینگی آنها ته کشیده بود. آنها تصمیم گرفتند تا لاگرانژ به تحصیل
حقوق بپردازد. او به دانشگاه تورین وارد شد و از تحصیل حقوق و ادبیات کلاسیک لذت
میبرد، ولی کلاسهای ریاضی، که بیشتر شامل آموزش هندسه اقلیدسی میشد، برایش کسل
کننده بود. سپس کتابی درباره روشهای جبری در نورشناسی اثر منجم انگلیسی ادموند
هالی بدست او رسید، و موجب شد تا تصورش بکلی در مورد ریاضیات تغییر کند. لاگرانژ
راهی را در پیش گرفت که تحقیقات اولیه او را تحتالشعاع قرار داد: کاربرد ریاضیات
در مکانیک، خصوصاً مکانیک سماوی.
او با یکی
از دختر عموهای خود بنام ویتوریا کونتی ازدواج کرد. او در این مورد برای دوست خود،
ژان دالامبر[98]، که او هم ریاضیدان بود، مینویسد: ”همسرم یکی از دختر عموهای من
است که مدتها با خانواده ما زندگی میکرد. او کدبانوی خیلی خوبی است و به هیچ وجه
هم اهل تظاهر نیست.“ او همچنین بطور محرمانه پیش دوست خود اعتراف کرد که دلش نمیخواهد
بچه دار شود، آرزوی که به تحقق رسید.
لاگرانژ
منصبی در برلین گرفت، مقالات تحقیقاتی بسیاری نوشت، و بارها برنده جایزه سالانه
آکادمی فرانسه شد – درسال 1772 در جایزه با اویلر شریک بود، در سال 1774
مقالات متععدی درباره دینامیک ماه نوشت و در سال 1780 بخاطر کارهایی که درباره
تاثیر سیارات بر ستارههای دنبالهدار کرده بود جایزه دریافت کرد. عشق دیگر زندگی
او نظریه اعداد بود و در سال 1770 او اثبات دیگر برای قضیه چهار مربع ارائه داد.
این قضیه میگوید که هر عدد مثبت صحیح را میتوان بصورت حاصل جمع مربع چهار عدد
صحیح دیگر نوشت. برای مثال 7=22+12+12+12+12
و 8=22+22+02+02 و به همین ترتیب.
او به
عضویت آکادامی علوم فرانسه درآمد و به پاریس نقل مکان کرد، جایی که عمرش را تا آخر
در آنجا سپری کرد. او عقیده داشت که شخص باید از قوانین کشوری که درآن زندگی میکند
پیروی کند، حتی اگر این قوانین مخالف رای او باشند، مسئلهای که باعث شد وی از
سرنوشتی که بسیاری از روشنفکران در دوران انقلاب فرانسه به آن دچار شدند در امان
بماند. لاگرانژ در سال 1788 شاهکار خود، مکانیک تحلیلی، را منتشر کرد. این
کتاب شاخه مکانیک را بعنوان شاخهای از آنالیز ریاضی مطرح میکرد. او همیشه به این
افتخار میکرد که کتاب حجیم او دارای هیچ نموداری نیست؛ از دید او منطق جای مهمتری
داشت.
در سال
1792 با همسر دومش رنه-فرانسو آدلاید لو موسیو، که دختر یک منجم بود ازدواج کرد.
در سال 1793، در دورانی که حکومت وحشت بر فرانسه حکمفرما بود، آکادامی بسته شد و
تنها بخشی که فعال بود اداره اوزان و مقیاسات بود. بسیاری از دانشمندان برجسته از
کار برکنار شدند، کسانی مثل: شیمیدان معروف لاوازیه، چارلز آگوستین کلمب و نیز پیر
سیمون لاپلاس که هر دو فیزیکدان بودند. لاگرانژ سرپرست جدید اداره اوزان و
مقیاسات شد.
در این
هنگام، مکان تولدش باعث بروز مشکلاتی برای او گردید. دولت انقلابی قانونی را به
تصویب رساند که در آن آمده بود هر خارجی که در یکی از کشورهای متخاصم بدنیا آمد
باید دستگیر شود. لاوازیه که در آن زمان هنوز کمی نفوز داشت، طوری قرار گذاشت که
لاگرانژ از این قانون معاف بماند. پس از چندی یک دادگاه انقلابی لاوازیه را به مرگ
محکوم کرد، و روز بعد با گیوتین اعدام شد. لاگرانژ در این مورد اظهار داشت ”تنها
یک لحظه طول کشید تا سر از تن او جدا شود، در حالی که صدها سال طول میکشد تا کسی
مانند او بدنیا آید.“
در طول
حکومت ناپلئون لاگرانژ بارها القابی را کسب کرد: در سال 1808 لژیون عالی و کنت
امپراطوری، و صلیب عالی اتحاد در سال 1813. او یک هفته پس از دریافت صلیب عالی
درگذشت.

در سال
1770، در همان زمانی که او قضیه چهار مربع را کشف کرده بود، مقالات زیادی درمورد
نظریه معادلات نوشت، او در مقدمه یکی از مقالات خود میگوید: ”در این مقاله من قصد
دارم تا روشهای مختلفی که تا کنون برای حل جبری معادلات یافت شده را مورد بررسی
قدار دهم، آنها را به اصول عمومیتری تنزل دهم، و شرح دهم که چرا این روشها که
برای معادلات درجه سوم و چهارم جواب میدهند، نمیتوانند برای معادلات درجه بالاتر
بکار روند.“ همانطور که ژان-پیر تینول در کتابش بنام نظریه گالوا برای
معادلات جبری آورده ”قصد لاگرانژ این بود که نه فقط مشخص کند چگونه این روشها
کار میکنند، بلکه چرایی آن را هم توضیح دهد.“
لاگرانژ
در قیاس با ابداع کنندگان روشهای رنسانسی، نسبت به روشهایی که آنها بکار میبردند
درک عمیقتری داشت؛ او حتی ثابت کرد که طرح کلی که آنها به آن دست یافتند، برای
معادلات درجه پنجم و بالاتر قابل استفاده نسیت. ولی با این حال او نتوانست قدمهای
بیشتری برای تکمیل موضوع بردارد که کلاً آیا هیچ راهحلی قابل حصول هست یا
نه. در عوض او به ما میگوید که ” برای کسانی که بخواهند با حل معادلات درجه بالا
سر وکار داشته باشند، نتایج حاصل در این مقاله، با فراهم آوردن نظرات گوناگون و
حذف مراحل بیفایده، سودمند خواهند بود.“
لاگرانژ
متوجه شد که تمام ترفندهایی که بوسیله کاردانو، تارتالیا و دیگران بکار میرفت فقط
بر پایه یک شگرد قرار داشت. آنها بجای اینکه سعی کنند ریشه معادله اصلی را بطور
مستقیم پیدا کنند، مسئله را به حل یک معادله فرعی (کمکی) تقلیل میداند، معادلهای
که ریشههای آن با معادله اصلی رابطه داشت ولی با آن فرق میکرد.
برای یک
معادله درجه سوم، معادله کمکی آن سادهتر بود، یعنی درجه آن 2 بود. این معادله
کمکیِ ”کارگشایِ درجه دوم“ بسادگی میتوانست با روشهای بابلی حل شود و بنابراین
معادله درجه سوم میتوانست تنها با یک ریشه سوم گرفتن از جواب معادله کمکی حل شود.
این دقیقاً ساختاریست که در فرمول کاردانو وجود دارد. برای معادله درجه چهارم،
معادله کمکی از نوع سادهتر از آن، یعنی درجه سوم، خواهد بود. این معادله کمکیِ
”کارگشایِ درجه سوم“ را میتوان با روشهای کاردانو حل کرد و سپس برای حل معادله
اصلی از آنها ریشه چهارم گرفت. این دقیقاً ساختاری است که در فرمول فراری برای حل
معادلات درجه چهارم وجود دارد.
ما
میتوانیم هیجان لاگرانژ را از این مسئله دریابیم. اگر این الگو به همین ترتیب
ادامه پیدا کند پس معادله کمکی برای یک معادله درجه پنج، از نوع درجه چهارم خواهد
بود که میتواند با روش فراری حل شود و درآخر برای حل معادله اصلی از آن یک ریشه
پنجم گرفته شود. و این رویه به همین ترتیب ادامه پیدا میکند، معادله درجه ششم به
معادله درجه پنجم تقلیل پیدا میکند، این معادله با روش حل معادله درجه پنجم حل میشود
(همینطور که بعداً خواهیم دید چنین روشی وجود ندارد). به این ترتیب او قادر بود تا
هر معادلهای را، از هر درجهای که باشد، حل کند.
ولی دیری
نپایید که وی از عرش فرود آمد. معادله کمکی برای معادله درجه پنجم درجه چهار نبود،
بلکه درجهای بالاتر داشت و یک معادله درجه ششم بود! روشی که میتوانست معادلات
درجه سوم و چهارم را به معادلاتی سادهتر تبدیل کند، معادله درج پنجم را دشوارتر
میکرد.
اگر هر
مسئلهای، بجای سادهتر شدن، با نوع سختتر آن جایگزین شود، ریاضیات هیچ پیشرفتی
نخواهد داشت. روش متحدکننده لاگرانژ در مورد معادلات درجه پنجم با شکست روبرو میشد.
ولی او هنوز ثابت نکرده بود که معادلات درجه پنجم را کلاً نمیتوان بوسیله
رادیکالها حل کرد، زیرا ممکن بود روشهای متفاوتی برای حل آن وجود داشته باشد که وی
از آنها بی خبر بود.
چرا که
نه؟
از نظر
لاگرانژ این سئوالی نبود که نیاز به پاسخ داشته باشد. ولی یکی از جانشینان او این
مطلب را جدی گرفت و به آن پاسخ داد.

نام او
پائولو روفینی[99] بود، و وقتی من قبلاً گفتم او به سئوال بیجواب لاگرانژ ”پاسخ
داد“، من کمی تقلب کردم. او پیش خود چنین فکر میکرد که به این سئوال
پاسخ داده، و معاصرین وی هم هیچ چیز اشتباهی در پاسخ او پیدا نکردند- شاید دلیلش
این بود که هرگز حوصله این را نداشتند تا بطور کامل استدلالات وی را بررسی کنند.
روفینی عمرش را با این فکر سپری کرد که توانسته ثابت کند که معادلات درجه پنجم
بوسیله رادیکالها قابل حل نیستند. تنها پس از مرگ او بود که معلوم شد یک نقص
اساسی در استدلال او وجود دارد. این نقص درمیان محاسبات پیچیده که در کلیه صفحات
مقالهاش موجود بود گم شده بود. این نقص بواسطه مفروض قرار دادن چیزی بود که بنظر
”واضح و صحیح“ میآمد، فرضی که او هرگز متوجه آن نشد.
همانطور
که هر ریاضیدان حرفهای برحسب تجربیات تلخش میداند، بسیار دشوار است که شما
متوجه فرض بیان نشدهای شوید، بصرف اینکه این فرض بصورت صریح بیان نشده باشد.
روفینی در
سال 1765 بدنیا آمد. پدرش یک طبیب بود. در سال 1783 او در دانشگاه مودنا ثبت نام
کرد و به مطالعه پزشکی، فلسفه، ادبیات و ریاضیات پرداخت. او هندسه را نزد لوئیجی
فانتینی و حسابان را نزد پائلو کاسینی یادگرفت. هنگامی که کاسینی برای دریافت
منصبی در خانواده اِسته، کرسی خود را خالی کرد، گرچه روفینی یک دانشجو بود، ولی
مسئولیت درسهای آنالیز کاسینی را برعهده گرفت. او درسال 1788 در رشتههای فلسفه،
پزشکی و جراحی مدارکی دریافت کرد و درسال 1789 مدرک ریاضی را نیز به آنها افزود.
اندکی بعد از آن، او کرسی استادی فانتینی را که چشمانش نابینا شده بود در اختیار
گرفت.
وقایع آن
زمان در کارهای او وقفه افکند. ناپلئون بوناپارت در سال 1796 قوای اطریش و
ساردینیا را شکست داد، نگاهش را بسوی تورین متوجه، و میلان را تصرف کرد. بزودی او
به مودنا رسید و روفینی مجبور بود تا در سیاست درگیر شود. او قصد داشت با بار
دیگر در سال 1798 به دانشگاه بازگردد، ولی بدلایل مذهبی از سوگند به جمهوری سرباز
زد. بیکاری موجب شد تا وی تحقیقات خود را ادامه دهد و توجه خود را روی مسئله
پردردسر معادلات درجه پنجم متمرکز کند.
روفینی
خود را متقاعد کرده بود که حتماً دلیل خوبی وجود دارد که کسی تا بحال نتوانسته
معادلات درجه پنجم را حل کند: دلیل این بود که اصلاً راهی برای حل آنها وجود
ندارد. مخصوصاً هیچ فرمولی، که فقط در آن از رادیکالها استفاده شده باشد، وجود
نداشت تا بتوان با آن معادلات درجه پنجم را بصورت عمومی حل کرد. در کتاب دو جلدی
خود بنام نظریه عمومی معادلات، که درسال 1799 منتشر کرد، روفینی ادعا کرد که
قادر به اثبات این مسئله است و اینطور نوشت: ”حل جبری معادلات درجه چهارم به بالا
همیشه غیر ممکن است. در نظر داشته باشید که قضیه بسیار مهمی وجود دارد که فکر میکنم
(اگر اشتباهی نکرده باشم) قادر به اثبات آن هستم. دلیل اصلی انتشار این کتاب هم
ارائه اثباتی برای این قضیه است. لاگرانژ کبیر، با آن تفکر تابناکش، بنیاد استدلال
مرا فراهم آورد.“
این
استدلال طولانی، بیش از 500 صفحه را اشغال میکرد، و محتوای آن پر از ریاضیات
ناآشنا بود. در نظر دیگر ریاضیدانان این کتاب هراس انگیز بود. حتی امروه هم کسی
اشتیاقی برای دنبال کردن یک استدلالِ فنیِ طولانی را ندارد، مگر اینکه دلایل خیلی
خوبی برای اینکار وجود داشته باشد. اگر روفینی اعلام کرده بود که برای معادلات
درجه پنجم راه حلی پیدا کرده، مطمعناً همکاران وی کوشش میکردند تا مطالب
وی را بهتر دنبال کنند. ولی شما میتوانید بخوبی دلیل بیمیلی آنها را برای صرف
صدها ساعت وقت درک کنید، زیرا ادعای مورد بحث جنبه منفی داشت.
کمتر چیز
ناراحت کنندهای ممکن است برای یک ریاضیدان وجود داشته باشد که در یک کتاب ریاضی
500 صفحهای، یک اشتباه پیدا شود، آنهم در صفحه 499 آن.
روفینی در
سال 1801 نسخهای از کتاب را برای لاگرانژ فرستاد، بعد از چند ماه سکوت او بار
دیگر نسخه دیگری برای او فرستاد، ولی اینبار کتاب یادداشتی به همراه داشت: ”اگر من
در استدلال خود خطایی مرتکب شدهام، یا اگر چیزی گفتهام که به باور خودم جدید
بوده، و در واقعیت اصلاً چیز جدیدی نبوده، و اینکه اگر نهایتاً کتابم را بیفایده
دانستید، از شما تقاضا دارم که آنرا صادقانه به من تذکر دهید.“. مدتی گذشت و باز
هم جوابی از طرف لاگرانژ نیامد. در سال 1802 باز هم نامهای فرستاد ولی هنوز هم
جوابی نبود.
چندین سال
بدون اینکه روش روفینی شناسایی شود سپری شد و روفینی احساس کرد که تقصیر از خود
اوست. شایعاتی در برخی محافل پخش شده بود که در ”اثبات“ او اشتباهاتی پیدا شده،
ولی چون کسی نمیگفت این اشتباهات چه میتوانند باشند، روفینی قادر نبود از خود
دفاع کند. بالاخره او فکر که شاید استدلالاتش پیچیده هستند و تصمیم گرفت که آنها
را به صورت سادهتری بیان کند. در سال 1803 وی چنین کاری را به انجام رساند و در
مقدمه آن نوشت ”در این مقاله من سعی خواهم کرد که قضیه قبلی را، بصورتی که کمتر
انتزاعی باشد، و با دقت کامل ارائه دهم.“ اثبات جدید دست کمی از قبلی نداشت. جهان
برای نوع نگرشی که روفینی ارائه میکرد، و یا برای اثباتهایی که در سالهای 1808 و
1813 منتشر کرد، آمادگی نداشت. او هیچ موقع از تلاش برای اینکه کارهایش مورد
شناسایی جامعه ریاضی قرار گیرد دست برنداشت. هنگامی که ژان دالامبر، که موقعیت
سیاره اورانوس را پیشبینی کرده بود، گزارشی در مورد وضعیت ریاضیات تا سال 1789
تهیه کرد و در آن این جمله را گنجاند که ”روفینی قصد دارد ثابت کند که حل معادلات
درجه پنجم غیر ممکن است.“ روفینی سریعاً جواب داد ”من نه فقط قصد اثبات این را
داشتهام، بلکه حقیقتاً آن را اثبات کردهام.“
اگر
بخواهیم صادق باشیم، ریاضیدانانی نیز بودند که از اثبات روفینی راضی بودند.
در میان آنها باید به کوشی اشاره کرد، که هر وقت صحبت بر سر اعتبار و قدرشناسی
بود، او همیشه از زیر بار آن شانه خالی میکرد، جزاینکه موضوع صحبت کارهای خودش
باشد. او در سال 1821 به روفینی مینویسد ”مقالات شما درباره حل عمومی معادلات
موضوعی است که همیشه برای من ارزشمد بوده، و بر این اعتقاد هستم که باید
ریاضیدانان به آن توجه داشته باشند، و از نظر من شما عدم امکان حل جبری معادلات
درجه چهارم به بالا را به اثبات رساندهاید.“ ولی در آن موقع برای تعریف و تمجید
خیلی دیر شده بود.
در حدود
سال 1800، روفینی به تدریس ریاضیات کاربردی در مدرسه نظامی شهر پرداخت. او به
طبابت نیز ادامه داد، و از بیمارانی از هر طبقه اجتماع، چه فقیر و چه غنی، مراقبت
میکرد. در سال 1814، بعد از سقوط ناپلئون او رئیس دانشگاه مودنا شد. در آن دوران
هنوز وضعیت سیاسی خیلی بغرنج بود، و علیرغم توانهاییهای شخصیاش، دوران ریاست او
بردانشگاه دوره سختی بود.
روفینی
همزمان در دانشگاه مودنا کرسی استادی ریاضیات کاربردی، داروشناسی و پزشکی بالینی
را دردست داشت. درسال 1817 در آن ناحیه بیماری تیفوس همهگیر شد، و روفینی
تا وقتی که خودش به این بیماری مبتلا نشده بود به معالجه بیماران مشغول بود. او از
این بیماری جان سالم بدر برد ولی هرگز سلامتی خود را باز نیافت، و در سال 1819
کرسی پزشکی بالینی خود را واگذار کرد. با این وجود او هیچگاه کارهای علمی خود را
مفوقف نکرد، و در سال 1820 مقالهای در مورد بیماری تیفوس منتشر کرد که در آن
تجربیات خود را هم بعنوان یک طبیب، و هم بعنوان یک بیمار مبتلا به این مرض ارائه
داده بود. او کمتر یک سال بعد از اینکه کوشی از کارهای او در مورد معادلات درجه
پنجم تمجید کرده بود، در سال 1822 از دنیا رفت.
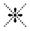
ممکن است
یکی از دلایل اینکه کارهای روفینی خیلی مورد توجه قرار نگرفت بدعت و تازگی آنها
بوده باشد . مانند لاگرانژ، او نیز کار خود را بر پایه ”جایگشت[100]“ بنا کرد. جایگشت روشی برای دوباره مرتب کردن یک فهرست است. معروفترین
مثالی که در اینمورد میتوان ارائه داد بُر زدن یک دسته ورق بازی است. هدف از
اینکار ایجاد نوعی ترتیب تصادفی است- منظور از ترتیب تصادفی، ترتیبی است که غیر
قابل پیشبینی باشد. تعداد جایگشتهای یک دسته ورق بازی بقدری زیاد است که شانس
پیشگویی وضعیت آنها پس از یک بُر خوردن تصادفی بسیار کم است.
جایگشتها
به این دلیل در نظریه معادلات مطرحاند که ریشههای یک معادله مفروض را میتوان
بعنوان یک فهرستی از اعداد درنظر گرفت. برخی از اساسیترین خصوصیات معادلات بطور
مستقیم با بُر زدن آن لیست (ریشههای معادله) مرتبت است. واقعیت آن است که معادله
از ترتیبی که شما برای ریشههای آن در نظر میگیرید ”آگاه نیست“، بنابراین
جایگزینی آنها با یکدیگر نباید هیچ گونه تفاوت مهمی در آن ایجاد کند. بویژه، ضرایب
معادله باید نسبت به ریشهها عبارات کاملاً متقارنی باشند، یعنی عباراتی که وقتی
در ریشهها جایگشتی بوجود آید تغییری در آنها بوجود نمیآید.
ولی
همانگونه که لاگرانژ دریافته بود، بعضی از عباراتِ ریشهها ممکن است نسبت به برخی
جایگشتها متقارن باشند و نسبت به بقیه نه. این عباراتِ ”نسبتاً متقارن“ بطور
نزدیکی با هر فورمولی که بخواهد معادله را حل کند وابستهاند. این ویژگی جایگشتها
برای همکاران روفینی آشنا بود. ویژگی که در این میان کمتر آشنا بود، استفاده اصولی
از یکی دیگر از ایدههای لاگرانژ، یعنی ضرب جایگشتها بود: در اینحالت شما میتوانید
دو جایگشت را در هم ”ضرب“ کنید تا جایگشت دیگری حاصل شود.
برای روشنتر
شدن مطلب سه علامت a, b , c را درنظر بگیرید. شش جایگشت مختلف برای این علامتها وجود دارد:
abc, acb, bac, bca, cab, cba
یکی از
آنها ، مثلاً cba ، را انتخاب کنید. درنظر اول این فقط یک لیست مرتب است که از میان سه
علامت انتخاب شده. ولی ما میتوانیم آن را بعنوان قاعدهای برای مرتب کردن
لیست اولیه، یعنی abc،
نیز در نظر بگیریم. در اینصورت قاعده به این شکل خواهد بود که ”ترتیب علامتها
وارونه شود.“ پ ما میتوانیم این قاعده را نه تنها در مورد این لیست، بلکه برای هر
لیست دیگری بکار بگیریم. مثلاً اگر آنرا در مورد لیست bca بکار ببریم، حاصل acb خواهد بود. بنابراین
مفهومی وجود دارد که حاکی از این است که :
cba
× bca= acb
اگر چند شکل رسم کنیم احتمالاً این ایده را، که برای
داستان ما جنبه محوری دارد، میتوان بصورت ملموستری نشان داد. در شکل زیر دو نمودار
برای جایگشتی که abc را به cba و به bca تبدیل میکند:
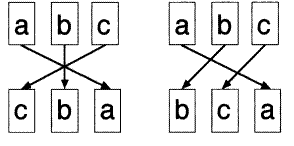
دو جایگشت
برای علامتهای a, b, c
با قرار دادن این دو تصویر در بالای یکدیگر ما میتوانیم
دو ترتیب فوق را با هم ترکیب کنیم. دو روش برای اینکار وجود دارد:
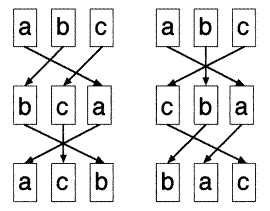
ضرب
جایگشتها در یکدیگر. نتیجه به این بستگی دارد که کدامیک در اول بیآید.
حالا
ما میتوانیم حاصل”ضرب“ این دو جایگشت را با نوشتن سطر پائینی بخوانیم (که برای
شکل سمت راستی bca و برای شکل سمت چپی acb
است). با این تعریف از ”ضرب“ (که با مفهوم معمول ضرب اعداد در یکدیگر متفاوت است)
ما میتوانیم عبارت acb = bca × cba
را درک کنیم. قاعده این است که اولین جایگشت در ضرب به پائین
دسته میرود. این مسئله اهمیت دارد زیرا با جابجا کردن ردیفها در دسته، ما از ضرب
آنها نتایج متفاوتی خواهیم گرفت. شکل سمت راستی تنایج ضرب جایگشتها را هنگامی که
بصورت برعکس در هم ضرب شوند نشان میدهد. نتیجه
bac = cba × bca
خواهد بود.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
ریاضیدانها
هیچ وقت راضی نمیشوند.
هر زمان
مسئلهای حل شود، حاصل آن تنها بوجود آمدن سئوالاتی جدید است. چیزی از مرگ آبل
نگذشته بود که جامعه ریاضی شروع به قبول استدلال او کرد، استدلالی دال بر اینکه
برخی معادلات درجه پنجم را نمیتوان بوسیله رادیکالها حل کرد. ولی کارهای آبل فقط
یک نقطه آغازین بود. گرچه کلیه تلاشهای قبلی برای حل کلیه معادله درجه
پنجم با شکست مواجه شده بود، با اینحال معدودی از ریاضیدانانِ بااستعداد اثبات
کردند که برخی از معادلات درجه پنجم را میتوان بوسیله رادیکالها حل کرد.
البته نه از نوع ساده و پیشپا افتادهای مثل x2-2=0 که جوابش x=![]() است، بلکه از نوع سختر آن، مثلاً x5+15x+12=0 . هرچند جواب این معادله
پیچیدهتر از آن است که بتوان آن را در اینجا ذکر کرد.
است، بلکه از نوع سختر آن، مثلاً x5+15x+12=0 . هرچند جواب این معادله
پیچیدهتر از آن است که بتوان آن را در اینجا ذکر کرد.
این قضیه
به معمایی بدل شده بود. اگر برخی از معادلات درجه پنجم را بتوان حل کرد و برخی را
نه، پس وجه تمایز میان این دو نوع در چیست؟
پاسخ به
این سئوال بود که مسیر ریاضیات، و فیزیک ریاضی، را تغییر داد. هر چند پاسخ این
سئوال بیشتر از 170 سال قبل داده شده، ولی هنوز هم موجب پیدایش کشفیات جدیدی میشود.
هنگامی که انسان به گذشته نگاه میکند، واقعاً شگفآور است که میبیند پرسش یک
سئوال بظاهر ساده ریاضی، چقدر میتواند پیآمدهای گستردهای داشته باشد. بنظر میرسید
که حل معادلات درجه پنجم هیچ فایده عملی نداشته باشد. اگر هم مسئلهای در مهندسی و
یا نجوم وجود داشت که به معادله درجه پنجم منجر میشد، روشهای عددی در دسترس بود
که میتوانستند با استفاده از آن جواب معادله را با هر دقتی که لازم بود تخمین
بزنند. حلپذیری (یا حلناپذیری) یک معادله درجه پنجم توسط رادیکالها نمونهای
کلاسیک از ”ریاضیات محض“ بود. به این دلیل به آن ”ریاضیات محض“ میگویند که
سئوالاتی را میپرسد که پاسخ آن فقط برای خود ریاضیدانها جالب است.
آبل مانعی
را که در حل برخی از معادلات درجه پنجم بوسیله رادیکالها وجود داشت کشف کرد. او
ثابت کرد که این مانع، حداقل برای برخی از معادلات درجه پنجم، حقیقتاً جلو وجود
چنین حلهایی را میگیرد. گام بعدی چیزی بود که کل داستان ما هم حول همان دور میزند،
و توسط کسی برداشته شد که دندان اسب پیشکشی را شمرد و سئوالی را پیش کشید که
ریاضیدانهای دیگر هم، موقعی که مسئله عمدهای حل میشود، وسوسه میشوند تا آنرا
بپرسند، آن سئوال شبیه این بود: ”خیلی هم خوب، دستتان درد نکند ... ولی لطفاً دلیل
ماجرا را توضیح دهید و اینکه چرا واقعاً اینطور است؟“
بنظر میرسید
که چنین رویکردی بیشتر منفی باشد، ولی بارها و بارها ثابت شده که پرسش چنین
سئوالاتی ارزش پرسیدن را دارد. اصل کلی این است که بیشتر مسائل ریاضیات مشکلتر از
آن هستند که کسی بتنهایی آنها را حل کند. بنابراین وقتی کسی پیدا شود و مسئلهای
را حل کند که موجب ناراحتی همه اسلاف خود بوده، تنها فقط شادمانی از اینکه چنین
راه حلی پیدا شده کافی نیست. دراین مواقع یا حلکننده مسئله خوششانس بوده
(ریاضیدانان به چنین شانسهایی اعتقاد ندارند) یا دلیلی دیگری باعث شده تا حل چنین
مسئله دشورای میسر شود. و اگر امکانی فراهم شود تا دلیل و چرایی اینگونه
مسائل فهمیده شود، ممکن است مسائل زیاد دیگری هم به این راهحلها جواب دهند و حل
شوند.
در همان
حینی که آبل مشغول پرداختن به این سئوال مشخص بود که ”آیا میتوان هر معادله درجه
پنجمی را حل کرد؟“ و به جواب واضح ”خیر“ هم دست یافت، متفکر دیگری، که حتی از او
نیز به مسائل عمقیتر نگاه میکرد، درحال دست و پنجه نرم کردن با سئوال کلیتری
بود: ”کدام معادلات را میتوان با رادیکالها حل کرد و کدام را نمیتوان؟“ اگر
بخواهیم انصاف را رعایت کرده باشیم، باید بگوییم که آبل هم در مورد چنین موضوعاتی
فکر کرده بود، و اگر سل به او امان داده بود، ممکن بود بتواند پاسخی برای آنها
پیدا کند.
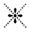
آن کسی که
مسیر ریاضیات و علم را تغییر داد، مرد جوانی بود بنام اواریستِ گالوا[109]، و داستان زندگی او یکی از مهیجترین، و همچنین غمانگیزترین
داستانها در تاریخ ریاضیات بحساب میآید. کشفیات شکوهمند او نزدیک بود بکلی گم
شوند.
اگر گالوا
زاده نمیشد، یا اگر حقیقتاً کارهای او مفقود شده بود، بدون شک، بالاخره کسی پیدا
میشد که کشفیات او را انجام دهد. بسیاری از ریاضیدانان همان خطوط فکری را دنبال
کرده بودند که گالوا از آن گذشته بود، و تنها یک گام با کشف اصلی فاصله داشتند.
شاید در جهانی دیگر، شخصی با استعداد و بینش گالوا پیدا میشد (کسی مثل آبل که
برای چند سالی از بیماری سل در امان مانده بود) و سرانجام به همان حلقههای فکری
نفوذ میکرد که او نفوز کرده بود. ولی جهان فعلی، این کار گالوا بود.
او در 25 اکتبر
سال 1811 در یکی از روستاهای اطراف پاریس، بنام بورژ-لا-راین[110]، بدنیا آمد. این روستا اکنون جزیی از حومه
پاریس، و مابین تقاطع بزرگراههای N20
وD60، قرار گرفته. بزرگراه
D60 اکنون خیابان گالوا
نامگذاری شده. در سال 1792 روستای بورژ-لا-راین (بمعنای شهر ملکه) به بورژ-لهاگالیته[111] (شهر مساوات)، تغیرنام یافت، نامی که منعکس کننده آشفنگی سیاسی و
ایدئولوژی دوران خود بود. در سال 1812، هنگامی که تا حدی از تب انقلاب کاسته شده بود،
نام روستا دو باره به نام قبلی خود بورژ-لا-راین بازگشت.
پدرش
نیکولاس-گابریل گالوا، یک جمهوریخواه، و رهبر حزب آزادی دهکده بود. هدف اصلی حزب
او واژگون سازی سلطنت بود. هنگامی که طی مصالحهای در سال 1814، لوئی هیجدهم
دوباره سلطنت را به فرانسه بازگرداند، نیکولاس-گابریل شهردار شهر شد، و با توجه به
تمایلات سیاسی او، ماندن در چنین منصبی کار راحتی نبود.
مادرش
آدلاید- ماری، در خانواده دِمنته بدنیا آمده بود. پدرش مشاور حقوقی و دستیار وکیل
بود. آدلاید در خواندن متون لاتین مهارت داشت و این آموزههای کلاسیک را به پسرش
یاد داد.
گالوا
دوازده سال اول عمرش را در خانه ماند، جایی که مادرش به او تعلیم میداد. هنگامی
که ده سال داشت در مدرسه ریمز برای او جایی در نظر گرفته شد، ولی بنظر مادرش او
کوچکتر از آن بود که خانه را ترک کند. ولی در اکتبر 1823 او به کالج لویی-لو-گران،
که بیشتر حالت پیشدانشگاهی را داشت، وارد شد. اندکی پس از ورود اواریست دانش
آموزان آنجا شروع به نافرمانی کرده و از خواندن سرود امتناع میکردند. اینجا بود
که گالوای جوان برای اولین بار سرنوشت انقلابی بودن را بچشم میدید: فوراً صدها
تن از دانشآموزان از مدرسه اخراج شدند. از بخت بدِ ریاضیات، این وقایع موجب درس
عبرتی برای او نشد.
در دو سال
نخست، او شاگرد اول درس لاتین بود، ولی پس از آن دیگر این درس برایش خسته کننده
شده بود. در نتیجه مدرسه اصرار کرد که او کالسهایش را تجدید کند تا نمرات بهتری
بگیرد، که البته این باعث شد تا این درس برای او ملالآورتر شود، و اوضاع از بد به
بدتر تغییر کرد. این ریاضیات بود که نگداشت گالوا در شیب تند تنبلی بلغزد. ریاضی
درسی بود که آنقدر محتوای فکری داشت که او را بخود جلب کند. ولی هر موضوعی هم،
توجه او را جلب نمیکرد. گالوا یک راست بسراغ اثر کلاسیک لُژاندر بنام اصول
هندسه رفت. این درست شبیه این است که امروز یک دانشجوی تازه وارد فیزیک شروع
بخواندن مقالات فنی انیشتین کند. ولی در ریاضیات یک نوع آستانه تاثیر وجود دارد.
اگر یک دانشجو بتواند سختیهای اولیه را پشت سر بگذارد، و این مسئاله را درک کند
که بهترین راه پیشرفت فهم ایدههاست، و نه حفظ کردن آنها، آنگاه چنین
دانشجویی قادر است مستقیماً از جاده فرعی به بزرگراه وارد شود، و بسوی ایدههای
پیچیدهتر و چالشبرانگیزتر حرکت کند، این درحالی است که یک دانشجوی کند ذهن در
فهم مثلث متساویالساقین هم گیر میکند.
هنوز
درباره اینکه چگونه گالوا توانسته بود اثر مهم لُژاندر را درک کند بحث وجود دارد،
ولی به هرحال این چیزی بود که وی هراسی از آن نداشت. او شروع بخواندن مقلات فنی
لاگرانژ و آبل کرد؛ جای تعجب هم نبود که آخرین کارهای او حول علاقه مشترک آنها،
بویژه نظریه معادلات، دور میزد. احتمالاً معادلات تنها چیزهای بود که توجه گالوا
را بخود مشغول کردند. وقتی را که او صرف ریاضیات میکرد به نسبت زیاد بود، و به
همین دلیل از درسهای دیگرش عقب افتاده.
گالوا در
مدرسه وضع نامرتبی داشت، عادتی که هرگز آنرا ترک نکرد. او بجای اینکه روی کاغذ
مسائل را حل کند و آن را به معلمینش نشان دهد، آنها را در ذهنش حل میکرد، کاری که
باعث عصبانیت آنها میشد. این یکی از طلسمهای معلمین ریاضی است که ممکن است
گریبانگیر بسیاری از جوانان با استعداد امروزی را هم بگیرد. تصور کنید که چه
اتفاقی میافتاد اگر یک فوتبالیست نوپا و بااستعداد هربار که گل میزد، مربی از او
میخواست که کلیه مراحل تاکتیکی که او برای بسمر رساندن گل طی کرده را بنویسد،
وگرنه گل او قبول نیست. در اینجور مواقع، اصلاً مرحلهای درکار نیست. بازیکن روزنهای
را میبیند و توپ را بجایی شوت میکند که هرکسی که این بازی را بلد است میداند
کجاست.
درمورد یک
ریاضیدانِ جوانِ بااستعداد نیز همینطور است.
جاهطلبی
گالوا باعث شده بود که قلهها را نشانه بگیرد: او میخواست مطالعات خود را در یکی
از معتبرترین دانشگاههای فرانسه، یعنی مدرسه پلیتکنیک، که پرورشگاه ریاضیات
فرانسه محسوب میشد، به انجام برساند. معلم ریاضی او سعی داشت تا وی را
وادار کند تا ایدههای خود را به طریق سازمانیافتهای ارائه کند که ممتحن بتواند
آنها را دنبال کند. ولی او به نصیحتهای او بیاعتنا بود. سرانجام اواریست با
اعتمادبنفسی بیش از حد، و با آمادگی اندکی در کنکور ورودی پلیتنیک شرکت کرد- و
مردود شد.
بیست سال
بعد، یک ریاضیدان پرنفوذ فرانسوی بنام اُرلی تِرکوئم[112]، که ویرایستار یک نشریه معتبر بود، دلیل
مردود شدن گالوا را چنین شرح میدهد: ”داوطلبی، با داشتن هوشی سرشار، در برابر
ممتحنی نهچندان باهوش شکست میخورد. درست مانند این است که بگویئم اگر حرف کسی را
درک نمیکنیم، پس آن شخص نادان است.“ یک مفسر امروزی که از لزوم مهارتهای ارتباطی
اگاهی بیشتری داشته باشد این انتقاد را کمی ملایمتر کرده و خواهد گفت که یک دانشآموز
باهوش باید برای کسانی که هوش کمتری دارند تلاش بیشتری صرف کند. در اینمورد، گالوا
با ناسازگاری که دربرابر دیگران نشان میداد، کمکی به درک آنها از خودش نمیکرد.
به ناچار
گالوا در مدرسه لوئی-لو-گراند باقی ماند، جایی که یک شانس نادر بسراغش آمد. معلمی بنام
لوئی-پُل ریچارد به استعداد مرد جوان پی برد، و گالوا در کلاس ریاضیات پیشرفتهای
که ریچارد تدریس میکرد ثبت نام کرد. ریچارد معتقد بود که گالوا بقدری بااستعداد
است که باید بدون آزمون وارد پلیتکنیک شود. هیچ مدرکی در دست نیست که آیا او این
نظر خود را با پلیتکنیک مطرح کرده یا نه. اگر هم که کرده باشد، آنها توجهای به
این موضوع نداشتند.
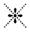
در اواسط
سال 1829 بود که گالوا اولین مقاله تحقیقاتی خود را، در زمینه کسرهای مسلسل، منتشر
کرد. این مقاله گرچه ارزنده بود ولی جذابیت خاصی نداشت. کارهای منتشر نشده او
بیشتر جاهطلبانه بود، زیرا این کارها نقش مهمی را در زیربنای نظریه معادلات ایفا
میکردند. او برخی از کارهایش را مرتب کرد و آنها را برای آکادمی علوم فرانسه
فرستاد تا شاید آن را در خبرنامه خودشان چاپ کنند. در آنروزها، و نیز هماکنون، هر
مقالهای که برای چاپ به دفتر آکادمی فرستاده میشد باید از طرف داوری که در آن
حوزه تخصص داشت مورد بررسی قرار میگرفت. وظیفه داور این بود که در مورد بدعت،
ارزش، و جالب بودن مقاله نظر بدهد. دراینمورد داور کوشی بود، که احتمالا
سرشناسترین ریاضیدان فرانسه محسوب میشد. انتخاب او بعنوان یک داور طبیعی بنظر
میرسید، زیر او خودش قبلاً در مورد موضوعات مرتبط با مقاله گالوا مطالبی را نوشته
بود.
بدبختانه
او آدم فوقالعاده گرفتاری هم بود؛ داستان رایجی در تاریخ ریاضیات هست که میگوید
کوشی دست نوشته گالوا را گم کرده؛ برخی از منابع به این اشاره میکنند که او با
انزجار مقاله را دور انداخته؛ ولی حقیقت ممکن است پیش افتادهتر از این باشد. نامهای
از کوشی در دست که به آکادامی نوشته و تاریخ آن به 18 ژانویه 1830 برمیگردد و در
آن او بخاطر اینکه گزارشی درمورد مقاله ”گالوای جوان“ ارائه نکرده عذرخواهی میکند
و شرح میدهد که کسالت داشته و در خانه بسر میبرده. او همچنین به
یادداشتهای خودش در اینمورد نیز اشاره میکند.
این نامه
مسائل متعددی را به ما میگوید. اول اینکه کوشی دست نوشته گالوا را دور نینداخته
بود و بعد از گذشت شش ماه از تحویل مقاله، هنوز آن را در اختیار داشت. و دوم اینکه
کوشی میباید دست نوشته را خوانده باشد که تصمیم گرفته بقدرکافی ارزشند هست که
توجه آکادمی را به آن جلب کند.
ولی در
جلسه بعدی که آکادمی برگزار شد کوشی بجای آن مقاله خودش را ارائه داد. چه بر سر
دستنوشته گالوا آمده بود؟
مورخ
فرانسوی رنه تاتون استدلال میکند که کوشی تحت تاثیر ایدههای گالوا قرار گرفته
بود (شاید هم کمی بیش از حد تحت تاثیر قرار گرفته بود). بنابراین بجای اینکه
همانطور که مرسوم بود مقاله اصلی را در آکادمی قرائت کند، او به گالوا توصیه کرد
که مقاله اصلاح شده و مفصلتری در تفسیر نظریه بنویسد تا برای دریافت جایزه بزرگ
ریاضی، که اقتخار عمدهای محسوب میشد، کاندید شود. هیچ سند معتبری برای تائید
چنین ادعایی موجود نیست، ولی ما میدانیم که در فوریه سال 1830 گالوا چنین مقالهای
را برای دریافت جایزه بزرگ ارسال کرده.
ما نمیتوانیم
از محتوای دقیق این مقاله مطمئن باشیم، ولی محتوای کلی آن را میتوان از روی آثار
باقیمانده گالوا استنتاج کرد. واضح است که اگر به کارهای گالوا بموقع ارج نهاده میشد
ممکن بود تاریخ طور دیگری رقم بخورد. درعوض دست نوشته او ناپدید شد.
یک توضیح
احتمالی برای این مسئله در سال 1831 در نشریه گلوب ((The Globe،
وابسته به جنبشهای
نو-مسیحی سوسیالیست موسوم به سن-سیمونیان[113]، مطرح شد. گلوب گزارش داد که پروندهای علیه
گالوا به اتهام سوء قصد علنی به جان پادشاه در دادگاه مطرح بوده و اعلان کرد ”این
یادداشتها ... شایسته دریافت جایزه بود، زیرا توانست برخی از مشکلاتی که لاگرانژ
از عهده حل آنها بر نیامد را حل کند. کوشی بالاترین تقدیرها را در مورد این موضوع
از نویسنده مقاله بعمل آورده. و در آخر چه شد؟ یادداشتها گم شد و جایزه به کس
دیگری غیر از این دانشمند جوان داده شد.“
مسئله
مهمی که باید در اینجا مد نظر داشت پایههای واقعی مقاله است. کوشی در سپتامبر
1830 برای پرهیز از رویارویی با انقلابیون از کشور گریخت، بنابراین مقاله نشریه
نمیتواند بر پایه هیچیک از سخنانی باشد که او بیان کرده. درعوض اینطور بنظر میرسد
که منبع اصلی خود گالوا بوده. گالوا دوست نزدیکی بنام آگوست شاوالیه داشت که از او
دعوت کرده بود به جمع سن-سیمونیان بپیوندد. بنظر میرسد که شاوالیه گزارشگر نشریه
بوده، و اگر چنین بوده باشد، این داستان باید از خود گالوا بیرون آمده باشد. یعنی
یا او این داستان را کلاً از خودش درآورده، و یا حقیقتاً کوشی کارهای وی را ستوده.
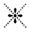
اجازه
دهید به سال 1829 بازگردیم. گالوا بدلیل اینکه میدید جامعه ریاضی، به آن میزان که
وی انتظارش را داشت قدر وی را نمیدانست، هر روز ناامیدتر میشد. از آن پس زندگی
شخصی او شروع به از هم پاشیدن کرد.
اوضاع در
دهکده بورژ-لا-راین خوب نبود. شهردار شهر، نیکولاس، که پدر گالوا بود، درگیر نزاع
سیاسی تندی شده بود که خشم کشیش دهکده را برانگیخته بود. کشیش با چاپ اعلامیههای
مختلف، موارد زنندهای را نسبت به نزدیکان نیکلاس پخش میکرد، و حتی امضاء خود
نیکولاس را هم در پای این اعلامیهها جعل کرده بود. نیکلاس از روی یاس، با خفه
کردن خودش، اقدام به خودکشی کرد.
این فاجعه
غمانگیز درست چند روز پیش از زمان امتحانات ورودی پلیتکنیک اتفاق افتاد. این
امتحان خوب پیش نرفت. برخی از روایات اشاره داردند که گالوا تختهپاککن را به
صورت ممتحن پرتاب کرده. (احتمالاً تختهپاککن پارچهای بوده و نه چوبی، ولی حتی
اگرهم چنین باشد، ممتحن خیلی از اینکار خوشحال نشده.) در سال 1899 جی. برتراند
جزئیاتی را برملا کرد که حاکی از این بود که از گالوا سئوالی پرسیده شده که انتظار
آن را نداشته و به همین دلیل عصبانی شده.
به هر
دلیلی که باشد، گالوا در امتحان ورودی مردود، و از آن پس دوچار گرفتاری شده
بود. او که به قبولی خود خیلی اطمینان داشته (از قرار معلوم او جوان متکبری
بوده)، به خودش زحمت نداده که برای ورودی تنها جایگزین ممکن پلیتکنیک، یعنی اکول
پرهپارتوار[114]، خودش را آماده کند. امروزه این دانشگاه اکول نورمال[115] نامیده میشود و اعتبار آن از پلیتکنیک بیشتر است، اما در آن
زمان در جایگاه دوم قرار داشت. گالوا بسرعت مواد لازم را خواند و دروس ریاضی و
فیزیک را با سربلندی کامل گذراند، دروس ادبیات را حسابی خراب کرد، و به هرصورت در
دانشگاه پذیرفته شد و در پایان سال 1829 صلاحیتهای لازم را هم در دروس علمی و هم
ادبیات کسب کرد.
همانطور
که ذکر کردم، در فوریه 1830 گالوا مقالهای را که در مورد نظریه معادلات نوشته
بود، جهت کسب جایزه بزرگ به آکادمی ارسال کرد. دبیر آکادامی، ژزف فوریه[116]، مقاله را به خانه برد تا نگاهی به آن بیاندازد. بار دیگر
بدشانسی سراغ گالوا آمد: فوریه درحالیکه هنوز مقاله را نخوانده بود درگذشت. بدتر
از آن، کسی نتوانست مقاله را در میان کاغذهای او پیدا کند. ولی سه نفر دیگر نیز در
کمیته اهدای جایزه عضویت داشتند: لوژاندر، سیلوستر-فرانسو لاکرو، و لوئی پونسوت.
احتمال این هست که یکی از آنها مقاله را گم کرده باشد.
دور از
انتظار نبود که گالوا عصبانی شود. او متقاعد شده بود که آنچه اتفاق افتاده توطئهای
است برای خاموش کردن یک نابغه؛ و فوراً گناه را بگردن رژیم ستمگر سلطنتی انداخت و
میخواست نقشی در سرنگون کردن آن بر عهده بگیرد.
شش سال
قبل، در 1824، شاه شارل دهم، پس از لوئی هجدهم به سلطنت فرانسه رسید. ولی او
پادشاه محبوبی نبود. مخالفین آزادیخواه در انتخابات 1827 آراء خوبی را بدست آوردند
و حتی در انتخابات 1830 موفق به کسب اکثریت آراء شدند. شارل که خود را با استعفای
اجباری مواجه میدید، دست به کودتا زد؛ در 25 ژوئیه او اعلامیهای مبنی بر تعلیق
آزادی مطبوعات صادر کرد. او رفتار مردم را، که بسرعت دست به تغیان زده بودند،
اشتباه تعبیر کرد، و بالاخره پس از سه روز مذاکره مصالحهای حاصل شد: شارل بعنوان
پادشاه جای خود را به دوکِ اورلئان، لوئی فیلیپ داد.
دانشجویان
دانشگاه پلیتکنیک، جایی که گالوا امیدوار بود در آن پذیرفته شود، با برگذاری
تظاهرات در خیابانهای پاریس، نقش مهمی را در حوادث آن دوران برعهده داشتند.
و گالوای ضد سلطنت ما در آن دوران شوم کجا بود؟ بهمراه بقیه همکلاسیهایش در داخل
دانشگاه اکول پرهپارتوار حبس شده بود. با اینکار رئیس دانشگاه تصمیم گرفته بود
آنجا را از شورش در امان نگاه دارد.
گالوا از
این مسئله که دیگران برای پرآوازه شدن او درتاریخ مانع تراشیده بودند! چنان خشمگین
بود که نامه تندی را در نشریه دانشگاه بر علیه رئیس دانشگاه منتشر کرد. ویرایستار
نشریه نامه او را چاپ کرد ولی امضاء وی را از پای آن حذف کرد. رئیس دانشگاه فوراً
گالوا را بعلت منتشر کردن یک نامه بینام و نشان اخراج کرد.
گالوا با
پیوستن به توپخانه گارد ملی، که یک سازمان مدافع جمهوری خواهی بود، اینکار را
تلافی کرد. این گروه، که به احتمال زیاد گالوا هم همراه آنها بود، در 21 دسامبر
1830 در نزدیکی لوور مستقر شدند. چهار وزیر سابق درحال محاکمه بودند و جو عمومی
ملتهب بود: مردم میخواستند که آنها اعدام شوند، و آماده بودند که اگر این اتفاق
نیفتد دست به شورش بزنند. ولی درست پیش از اینکه رای نهایی صادر شود، توپخانه گارد
ملی با نگهبانان عادی و دیگر سربازان وفادار به پادشاه جایگزین شدند. حکم زندان
برای وزراء صادر شد، شورشی نیز صورت نگرفت، و ده روز بعد هم توپخانه گارد ملی
بدلایل امنیتی توسط پادشاه جدید، لویی-فیلیپ، منحل اعلام شد. گالوا در انقلابیگری
هم به همان اندازه موفق بود که در ریاضیدان بودن.
حالا دیگر
موارد روزمره برای او ضرورت بیشتری از سیاست داشت: او میباید زندگی کند. گالوا
خود را آماده میکرد تا بصورت خصوصی ریاضیات تدریس کند، و چهل دانش آموز برای دوره
جبر پیشرفته او ثبت نام کردند. ما میدانیم که گالوا از نظر توضیح و تشریح
موضوعات، نویسنده خوبی نبوده، و معقول است که نتیجه بگیریم که معلم چندان خوبی هم
نبوده است. احتمالاً کلاسهای او با جر و بحثهایی مخلوط شده بود؛ و احتمال قریب به
یقین این کلاسها برای آدمهای معمولی خیلی دشوار بوده. به هر حال تعداد شاگردان
کلاس بسرعت کم شد.
گالوا
هنوز هم حرفه ریاضی خود را کنار نگذاشته بود، و نسخه سوم کار خودش، تحت عنوان ”درباره
شرایط حلپذیری معادلات بوسیله رادیکالها“را به آکادامی ارسال کرد. حالا که
کوشی از پاریس گریخته بود، داوران انتخاب مقاله سیمئون پواسون[117] و لاکرو بودند. وقتی دو ماه گذشت و خبری
نشد، گالوا نامهای نوشت و علت را جویا شد. باز هم کسی پاسخ نداد.
از بهار
1931 به بعد رفتار گالوا غیرمعقولتر میشود. سوفی جرمین[118]، که با تحقیقاتی که در سال 1804 شروع کرد
گاوس را خیلی تحت تاثیر قرار داد، طی نامهای به گ. لیبری درباره گالوا اینطور
مینویسد: ”آنها میگویند که او بکلی دیوانه شده، و من میترسم که این موضوع حقیقت
داشته باشد.“ گالوا که هیچ موقع شخص باثباتی نبود، حالا در آستانه جنون و
سوء ذن کامل بود.
در آن
ماه، مقامات دولتی نوزده عضو توپخانه را بعلت حوادث لوور دستگیر، و آنها را بدلیل
اغتشاش محاکمه کردند. ولی هیئت منصفه آنها را تبرئه کرد. توپخانه در روز 9 ماه مه
جشنی برپا کرد که در آن حدود دویست تن از جمهوریخواهان در رستورانی دور هم جمع
شدند. همه آنها خواستار سرنگونی لوئی-فلیپ بودند. نویسنده معروف آلکساندر دوما که
در آن جمع حاضر بود نوشت ”در تمام پاریس مشکل میتوان جایی را پیدا کرد که در آن
دویست نفر جمع باشند، که تا این حد نسبت به دولت خصومت داشته باشند.“ همانطور که
حوادث لگام گسیخهتر میشد، مردم گالوا را میدیدند که در یک دستش بطری شکسته بود و
در دست دیگرش یک خنجر. شرکت کنندگان در آن گردهمآیی این حرکت را تهدیدی نسبت به
پادشاه تلقی، و یکصدا از او پشتیبانی میکردند، حرکتی که به رقص در خیابانها منتهی
شد.
صبح روز
بعد گالوا در خانه مادرش دستگیر شد، و به متهم به این شد که قصد داشته به جان شاه
سوء قصد کند. بنظر میرسد که او برای نخستین بار سیاست بازی را یادگرفته باشد، زیرا
در جلسه محاکمهاش تمام چیزها را پذیرفت جز یک تعدیل کوچک: او ادعا کرد که وی
داشته جامش را به سلامتی لوئی-فیلیپ بالا میبرده، و در همین حال خنجرش را تکان
داده. او خیلی اظهار تاسف کرد که این حرکت او باعث شده تا مردم هلهله کنند و فریاد
بکشند.
ولی با
این حال گالوا تصریح کرد که او انتظار داشت که لوئی فیلیپ به مردم فرانسه خیانت
کند. او با سخنان خود جایی برای شک نگذاشت که منظورش این است که ”با تمایلاتی که
این حکومت دارد، هر کسی میتواند بفهمد که لوئی-فیلیپ، اگر هم که قبلاً اینکار را
نکرده باشد، بالاخره روزی به ملت خیانت خواهد کرد.“ باوجود این هیئت منصفه وی را
تبرئه کرد. شاید آنها همان چیزی را حس کردند که او گفته بود.
گالوا در
پانزدهم ژوئن آزاد شد. سه هفته بعد آکادامی در مورد مقاله او گزارشی بیرون داد. در
این گزارش پواسون مقاله او را ”غیر قابل فهم“ توصیف کرده بود:
”ما تمام
تلاش خود را کردیم تا اثبات گالوا را درک کنیم. استدلالات او واضح نیستند، و به
اندازه کافی توسعه داده نشدهاند تا ما بتوانیم در مورد صحیح بودن آنها قضاوت
کنیم.“
بدبختانه
مهمترین وجه این گزارش این است که امکان دارد حق با داوران بوده و در کل گزارش
صحیح و بیطرفانه بوده باشد. همانطور که داوران در گزارش خود مینویسند:
” آنگونه
که از عنوان مقاله پیداست، یعنی شرایط حل پذیری معادلات بوسیله رادیکالها، حتی
اگر بر اساس آنچه که آقای گالوا هم ادعا میکند درست باشد، کسی نمیتواند به روش
درستی تعیین کند که آیا یک معادله با درجه متشکل از اعداد اول، آیا بوسیله رادیکالها
قابل حل هست یا نه، زیرا اول باید مشخص کند که آیا معادله تحویل ناپذیر هست و سپس
معین کند که هر یک از ریشههای آن میتوانند بصورت کسر گویایی از دو ریشه دیگر
نمایش داده شود.“
در اینجا
جمله آخری به ضابطه زیبایی برای حلپذیری معادلات درجه اول بوسیله رادیکالها، که
اوج مقاله گالوا است، اشاره دارد. حقیقتاً مشخص نیست که چگونه میتوان این آزمون
را برای هر معادله بخصوصی انجام داد، زیرا شما قبل از انجام آزمون باید ریشه
معادله را بدانید. ولی بدون در دست داشتن یک فرمول برای حل معادله، شما چگونه
میتوانید ریشههای یک معادله را ”بدانید“؟ همانگونه که تینول میگوید ”نظریه
گالوا با آنچه از آن انتظار میرفت تطبیق نداشت.“ داوران انتظار داشتند که
بتوان از روی ضرایب معادله شرایطی را بدست آورد که تعیین کننده حلپذیری
معادله باشد؛ گالوا شرایطی را میداد که به ریشههای معادله بستگی داشت.
انتظار داوران نابجا بود. هیچ ضابطه سادهای که تنها بر اساس ضرایب معادله باشند
هرگز یافت نشده، و به احتمال قوی یافت هم نخواهد شد. ولی این واقعیت، کمکی به
گالوا نکرد.
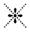
در 14
جولای، در روزی که به روز باستیل معروف است، گالوا و دوستش ارنست دوشاتله[119] در ردیف جلو تظاهرکنندگان جمهوری خواه بودند. گالوا درحالی که
یونیفرم افراد توپخانه منحله را بتن کرده بود، در دستش یک چاقو و در دست دیگرش یک
تپانچه گرفته و تُفنگ پُری را بر دوش انداخته بود. در آنروزها پوشیدن این یونیفرم و
حمل سلاح ممنوع بود. هر دو مرد در پون-نیوف دستگیر و گالوا به جرم پوشیدن یونیفرم
ممنوعه متهم شد. آنها تا روزه شروع محاکمه به بازداشتگاه سان-پلاژیه فرستاده شدند.
دوشاتله
در طول مدتی که در زندان بود، روی دیوار سلولش عکسی از سر پادشاه کشیده بود که در
زیر آن نوشته شده بود ”این سر زیر گیوتین میرود“. مطمعناً چنین رفتاری کمکی به
پرونده آنها نمیکرد.
ابتدا
دوشاتله محاکمه شد، و سپس نوبت گالوا رسید. در روز 23 اکتبر او محاکمه، و محکوم
شناخته شد؛ درخواست تجدید نظر او در روز 3 دسامبر رد شد. تا آن تاریخ او مدت چهار
ماه را در زندان سپری کرده بود. حالا او به شش ماه دیگر نیز محکوم شده بود. او
برای مدتی به کارهای ریاضی خودش پرداخت؛ سپس در هنگام شیوع وبای 1832 به بیمارستان
منتقل، و عفو مشروط شامل حالش شد. او در طول دوران آزادیش، اولین و تنها ماجرای
عشقی زندگی خود را با شخصی که در تاریخ به ”استفانی د.“ معروف است تجربه کرد.
از این
تاریخ به بعد، بدلیل کمبود شواهد تاریخی، باید به حدس و گمانهزنی متوسل شد. برای
مدتی کسی نمیدانست که اسم خانوادگی استفانی چیست و یا اینکه او چگونه آدمی بوده.
این معما به تصورات عاشقانهای که از او موجود بود افزود. گالوا در یکی از دست
نوشتههای خود نام کامل او را نوشته بود، ولی بعداً آنرا آنقدر خط خطی کرده بود که
قابل خواندن نبود. تحقیقاتی که بعداً توسط مورخی بنام کارلوس اینفانتوزی[120]، که بدقت دست نوشتهها را مورد بررسی قرار داد، انجام گرفت مشخص
کرد که نام آن زن استفانی-فلسیتی پوترین دو موتل[121] بوده. پدرش ژان-لویی، پزشک محله سیور فالتیه
بود، همان جایی که گالوا آخرین ماههای زندگی خود را در آنجا سپری کرد.
ما نمیدانیم
که نظر ژان-لویی در مورد رابطه دخترش با گالوا چه بوده، ولی محتمل بنظر نمیرسد که
او از رابطه دخترش با یک جوان بیپول، بیکار، سابقه دار، و فوقالعاده خشن، خیلی
راضی بوده باشد.
آگاهی ما
در مورد دیدگاههای استفانی نیز کم است، و تنها چیزی که از وی اطلاعاتی به ما
میدهد از روی جملات ناخوانای است که گالوا از نامههای منتسب به او کپی برداری
کرده. اسرار زیادی در مورد این دوره از زندگی گالوا هست که رابطه مهمی با حوادث
آتی دارد. ظاهراً دختر دست رد بر سینه گالوا زده، و از این باببت او خیلی ناراحت
شده، ولی شرح وقایع را نمیتوان درست تعیین کرد. آیا تمام این ماجرا چیزی بود که در
خیال او بود، مثلاً نوعی شیفتگی که هیچ وقت پاسخی به آن داده نشد؟ آیا استفانی از
او دلسرد شده بود؟ همان خصوصیاتی که موجب بیزاری پدر بود، ممکن است مخصوصاً برای
دختر جذاب بوده باشد.
از نظر
گالوا این رابطه حقیقتاً جدی بود. در ماه مه او به دوستش شاوالیه مینویسد ”چطور
میتوانم خود را دلداری دهم ، آن هم در زمانی که طی یک ماه، بزرگترین مایه شادی که
هر مردی میتواند داشته باشد را از دست دادهام؟“ در پشت یکی از کاغذهایش، او
قسمتهای از نامههای استفانی را نقل میکند. یکی از آنها با این جمله شروع میشود:
”لطفاً بگذار به این قضایا پایان دهیم،“ که نمایانگر این است که چیزی بوده که باید
به آن پایان داد. ولی نامه اینطور ادامه پیدا میکند ”و به چیزهای فکر نکن که وجود
ندارند، و هچ وقت هم وجود نداشتهاند.“ این جمله خلاف فرض قبلی است که مبنی بر
وجود رابطه بود. در جایی نیز آمده ”من نصیحت شما را گوش کردم و به چیزهایی فکر
کردم که ... اتفاق ... افتاده بود ... به هر حال مطمئن باشید آقا که دیگر چنین
چیزهایی اتفاق نخواهد افتاد. شما اشتباه فرض کردهاید و پشیمانی شما بیاساس است.“
اینکه آیا
او همه اینها را در خیال خود پرورانده و هیچ موقع به احساساتش پاسخی داده نشده، یا
اینکه در اوایل به نوعی تشویق میشده و بعدها رد شده، درست معلوم نیست، ولی اینطور
که بنظر میرسد گالوا دچار بدترین نوع عشق، یعنی عشق یکطرفه بوده. یا شاید هم کل
ماجرا بیشتر گمراه کننده بوده؟ اندکی پس از پایان رابطه با استفانی، ِیا آنچه به
نظر گالوا یک پایان رابطه میآمد، مردی با دعوت او به دوئل، گالوا را به مبارزه
طلبید. از شواهد ظاهری اینطور برداشت شده که این شخص میخواسته مانع نزدیکی گالوا
به زن جوان شود، ولی بار دیگر تکرار میکنم که شرح وقایع در پردهای از ابهام قرار
دارد.
حکایت
مرسوم حاکی از یک دسیسه سیاسی بود. اشخاصی نظیر اریک تمپل بل[122] و لوی کولروز[123] عقیده دارند که مخالفین سیاسی گالوا، شیفتگی
او نسبت به دوشیزه دو موتل، دستاویز خوبی برای حذف دشمن خود پیدا کردند، تا آنرا
یک نزاع ”ناموسی“ جلوه کنند. نظر حساب نشده دیگری هم هست که میگوید گالوا قربانی
جاسوس بازی پلیس شده بود.
حالا این
نظریات نامحتمل بنظر میرسند. دوما در خاطرات خود میگوید که گالوا توسط شخصی بنام
پشو دهربینول[124] که یکی از همرزمهان جمهوریخواه او بود، کشته شد. دهربینول از
نظر روستایان یک قهرمان بحساب میآمد. او یکی از نوزده نفری بود که از اتهام توطئه
برای براندازی حکومت تبرئه شدند. قطعاً او یک جاسوس پلیس نبود، زیرا هنگامی که در
سال 1848 مارک کاسیدیره به سمت رئیس پلیس برگزیده شد، نام تمام این جاسوسان
را افشاء کرد.
گزارش
پلیس حاکی از آن بود که طرف دیگر دوئل یکی از همرزمان انقلابی گالوا بوده، و دوئل
نیز همان چیزی بوده که از ظاهر آن برمیآمده. این نظریه عمدتاً بر پایه سخنانی است
که خود گالوا در باره موضوع بیا کرده: ”از تمام میهنپرستان و دوستان خود عذر میخواهم
که مرا برای اینکه در راهی غیر از میهن کشته شدم ببخشند. من قربانی زن بدنامی شدم.
زندگی من در چنین جنجال مصیبتباری به پایان میرسد. اه! چرا باید برای چنین چیز
پوچ و حقیری مُرد ... برای آنانی که مرا کشتند طلب آمرزش میکنم، آنها مردمان
شریفی هستند.“ او یا نمیدانسته که قربانی یک دسیسه سیاسی بوده، و یا اصلاً
دسیسهای درکار نبوده.
بنظر
میرسد که به احتمال زیاد استفانی دلیل اصلی دوئل بوده. گالوا قبل از عزیمت به مکان
دوئل کلمات بیربطی را بر روی تخته سیاهش نوشته بود، از جمله عباراتی نظیر ”یک زن“
که کلمه دوم آن خطخطی شده بود. ولی دلیل نهایی این قضیه نیز مانند بقیه ماجراهایی
که پیرامون داستان گالوا قرار دارد مبهم است.
داستان
ریاضی گالوا خیلی روشنتر است. در 29 ماه مه، در شب دوئل، گالوا در نامهای به
دوست خود آگوست شوالیه، خلاصه کشفیات خود را توضیح میدهد. سرانجام شوالیه این نامه
را در نشریه Revue
Encyclopedique چاپ می کند. در این نامه به ارتباط بین گروهها و
معادلات چندجملهای اشاره میشود، و در آن شرطی لازم و کافی برای حلپذیری معادلات
توسط رادیکالها بیان میشود.
گالوا در
این نامه به نظرات خود درباره توابع بیضوی و انتگرال گیری توابع جبری، و برخی
موارد نامشخص، نیز اشاره میکند. عبارت ”وقتی برایم نمانده“ که در حاشیه نامه
نوشته شده حاکی از افسانه دیگریست: اینکه گالوا شب قبل از دوئل را تا صبح بیدار
بوده و بطور دیوانهواری کشفیات ریاضی خود را بر روی کاغذ مینوشته. ولی عبارتی در
کنار آن عبارت آمد که میگوید ”یادداشتهای مؤلف“، و با فرضیه قبلی جور نیست؛ بعلاوه
این نامه شرحی بر سومین مقاله گالوا است که رد شد و با حواشی که پواسون به آن
اضافه کرد تکمیل میشود.
دوئل با
تپانچه انجام گرفت. در گزارش کالبد شکافی که بعداً انجام گرفت آمده که تپانچه از
فاصله 25 قدمی شلیک شده، ولی ممکن است حقیقت حتی بدتر از این باشد. در مقالهای که
در 4 ژوئن 1832 در نشریه
Le Precursor چاپ شده آمده است:
”پاریس،
یکم ژوئن – روز گذشته در طی یک دوئل اسفناک، جوانی که از او انتظارات فراوانی میرفت،
ولی اخیراً شهرت او بیشتر تحتالشعاع فعالیتهای سیاسی او قرار گرفته بود، از دست
رفت. اواریست گالوای جوان ... با یکی از دوستان قدیمی خود، که مانند خود او عضو
جامعه دوستان خلق بود و محاکمه نیز شده بود، درگیر نزاعی مهلک شد. آنگونه که گفته
میشود عشق دلیل دعوا بوده. از طپانچه بعنوان سلاح دوئل استفاده شده، ولی چون دو
حریف از دوستان قدیمی یکدیگر بودهاند سلاحهای یکدیگر را بررسی نکردهاند. آنها
در فاصله کمی نسبت بهم ایستاده، و از همین فاصله نیز شلیک کردهاند. تنها یکی از
تپانچهها آتش شده. بدن گالوا با گلولهای که حریفش شلیک کرده کاملاً سوراخ شده؛
او را به بیمارستان کوشین منتقل کردند و او حدود 2 ساعت بعد فوت کرد. او 22 ساله
بود. حریف او L.D
کمی از او جوانتر بود.“
آیا ”L.D“ میتواند اشارهای به ”پشو
دهربینول (Pescheux d'Herbinville)“
باشد؟ ممکن است. حرف D
قابل قبول است؛ حرف L
نیز ممکن است اشتباه باشد. جزئیات این مقاله قابل اتکا نیست؛ بخاطر اینکه اولاً
تاریخ دوئل را اشتباه چاپ کرده، و ثانیاً تاریخ فوت گالوا و سن او نیز اشتباه است.
بنابراین ممکن است بیشتر مقاله نیز اشتباه باشد.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
حالا دیگر
تقارن یک ایده مبهم نبود که در قالب نظم، و یا احساس ظرافت و زیبایی یک اثر هنری
تعریف شود. تقارن یک مفهومِ روشنِ ریاضی بود، با تعریفی محکم و منطقی. شما میتوانستید
روی تقارنها محاسباتی را انجام دهید، و یا در رابطه با آنها قضایایی را اثبات
کنید. یک شاخه جدید در ریاضیات بوجود آمده بود که نظریه گروها نام داشت.
جستجوی بشر برای تقارن به نقطه عطفی رسیده بود. بهای قبول این پیشرفت، تمایل هرچه
بیشتر به ”مفهومی فکر کردن“ بود. مفهوم گروه یک ایده انتزاعی (تجریدی) بود، مفهومی
که باید آن را در ردیف مفاهیمی چون اعدا و اشکال جای داد.
با حل
مسائلی چون حلپذیری معادلات درجه پنجم، گروهها ارزش خود را نشان داده بودند.
بزودی معلوم شد با بهرهگیری از همین نوع ایدهها میتوان به بسیاری از مسائل
قدیمی دیگر نیز رسیدگی کرد. شما در کارهای خود همیشه به نظریه گروهها نیاز
ندارید، ولی لازم است تا مانند آبل، گالوا، و دیگرانی که بعد از آنها آمدند،
فکر کنید. و حتی در مواقعی که فکر میکنید در حال استفاده از گروهها نیستید، آنها
معمولاً در پسزمینه و بطور پنهانی کار خود را انجام میدهند.
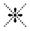
از میان
مسائل حلنشده که هندسهدانان یونان برای آیندگان به ارث گذاشتند، سه تای آنها
خیلی معروف شدند: مسئله تثلیث زاویه[133]، تضعیف مکعب[134]، و تربیع دایره[135]. حتی امروز نیز، مسائلی نظیر تثلیث زاویه و
تربیع دایره توجه بسیاری از علاقهمندان غیر حرفهای ریاضیات را به خود جلب میکند.
این دسته از افراد آماتورهایی هستند که بنظر میرسد هنوز باور نمیکنند که وقتی
ریاضیدانان میگویند حل فلان مسئله ”غیر ممکن است“، کاملاً در حرف خود جدی هستند.
بنظر میرسد مسئله تضعیف مکعب جاذبه بقیه را نداشته باشد. اغلب از این سه، بعنوان
”سه مسئله باستانی“ نام میبرند، ولی این عبارت اهمیت آنها را بیش از حد جلوه میدهد
و باعث میشود تا در رده مسائل غامض تاریخی، نظیر آخرین قضیه فرما که برای مدت 350
سال بدون پاسخ مانده بود، قرار گیرند. ولی آخرین قضیه فرما مشخصاً بعنوان یک مسئله
لاینحل شناخته میشد، و امکان این هست که دقیقاً زمانی را مشخص کرد که این مسئله
برای اولین بار در نوشتهجات ریاضی مطرح شده، و اینکه چه کسی آنرا مطرح کرده. کلیه
ریاضیدانان نه تنها از این مسئله آگاه بودند بلکه جواب احتمالی آنرا نیز میدانستند.
مسائل
یونانی متفاوت بودند. شما در آثار اقلیدس چیزی بنام مسائل حل نشده، که نیازمند
رسیدگی آیندگان است، را مشاهد نمیکنید. این مسائل عمدتاً از روی ناچاری بوجود
آمدهاند: آنها گسترشِ آشکار نتایج خاصی هستند، که بنا به دلایلی اقلیدس از آنها
پرهیز میکرد. چرا؟ برای اینکه کسی نمیدانست چگونه باید آنها را حل کند. آیا یونانیها
با خود فکر نکرده بودند که ممکن است این مسائل قابل حل نباشند؟ اگر هم که چنین
بوده، زیاد کسی صدای آنرا در نیاورد. بدون شک به ذهن کسانی مانند ارشمیدس رسیده
بود که این مسائل را نمیتوان با خط کش و پرگار حل کرد، دلیلش هم این است که او
برای این نوع مسائل راهحلهای دیگری پیدا کرده بود، ولی مدرکی در دست نیست که اصل
موضوع ”قابلیت ساخت با خطکش و پرگار“ برای او اهمیتی داشته است.
بعدها بود
که چنین چیزهایی اهمیت پیدا کردند. فقدان راهحل برای این نوع مسائل، به شکاف
عمیقی در فهم انسان از هندسه و جبر اشاره میکند؛ اینها بعنوان ”فرهنگ عامه ریاضی“
رواج پیدا کردند و آن زمانی که حل شدند از اهمیت ریاضی و تاریخی خاصی برخوردار
شدند. حل آنها بنظر خیلی مهم میآمد (مخصوصاً مسئله تربیع دایره)، و در مورد هر سه
مسئله جواب یکی بود: ”نمیتوان اینکار را کرد“. (حداقل با ابزارهای سنتی مثل خطکش
و پرگار نمیشود اینکارها را انجام داد.)
این مورد
ممکن است منفی بنظر آید، زیرا در بیشتر قدمهایی که انسان برای زندگی برمیدارد، در
جستجوی پاسخی برای سئوالات، و یا چیره آمدن بر مشکلات است، حال به هر شکل که میخواهد
باشد. اگر نتوان یک عمارت بلند را با آجر و ساروج ساخت، مهندسین از تیر آهن و بتنآرمه
استفاده میکنند. از اثبات اینکه نمیتوان کار را با آجر انجام داد کسی به
شهرت نرسیده.
ولی
ریاضیات شباهت زیادی به این موارد ندارد. محدودیت ابزارها اغلب همانقدر اهمیت دارند
که کارهایی که میتوان با آنها انجام داد. اهمیت سئوالات ریاضی اغلب به جواب آنها
بستگی ندارد، بلکه به این اهمیت دارد که چرا پاسخ صحیح است. برای سه مسئله باستانی
نیز همینطور بود.

حل کننده
مسائل سهگانه در سال 1814 در پاریس بدنیا آمد و نام او پییر لورنت وَنتزل[136] بود. پدرش در ابتدا افسر ارتش بود که بعداً استاد ریاضیات کاربردی
مدرسه عالی بازرگانی شد. پییر دانشآموزی تیز هوش بود، ژان کلود دِ سانونانت[137]، که ونتزل را میشناخت در مورد او چنین مینویسد ”او پسری بود که
استعداد خودش در ریاضیات را نشان داده بود. ریاضیات موضوعی بود که او با حرارت
بسیاری در مورد آن مطالعه میکرد. او بزودی حتی از استادان خودش جلو افتاد.“
پییر در
سال 1828 با موفقیت در آزمون ورودی کالج شارلمان پذرفته شد. او در سال 1831 برنده
جایزه اول درسهای لاتین و فرانسه شد، و نیز اولین کسی بود که هم در کنکور مدرسه
پلیتکنیک شاگرد اول شد و هم در مدرسه نورمال، کاری که پیش از او کسی نکرده بود.
او تقریباً به همه چیز علاقه داشت: ریاضیات، موسیقی، فلسفه، تاریخ، و از هیچ چیزی
بهاندازه یک بحثوجدل تند لذت نمیبرد.
در سال
1834 او توجه خودش را به مهندسی معطوف کرد، و در دانشکده پون اِ شاسیاس ثبت نام
کرد. ولی بزودی پیش دوستانش اعتراف کرد که او با اینکار چیزی جز یک ”مهندس معمولی“
نخواهد شد. او تصمیم گرفت تا معلم ریاضی شود و از دانشکده مرخصی گرفت. این تغییر
جهت خوب جواب داد: او در سال 1838 مدرس آنالیز در دانشگاه پلیتکنیک شد،
همچنین تا سال 1841 استاد کرسی ریاضیات کاربردی در دانشکده مهندسی هم شد.
سان-ونانت نوشت ”او عمولاً شبها کار میکرد و تا دیر وقت به بستر نمیرفت، سپس کمی
مطالعه میکرد، چند ساعتی به خواب میرفت، در مصرف قهوه و تریاک زیاده روی میکرد، و
تا وقتی ازدواج نکرده بود غذایش را بصورت نامرتب میخورد.“ او با دختر معلم زبان
لاتین خودش ازدواج کرد. وَنتزل آثار روفینی، آبل، گالوا و گاوس را مطالعه کرد و
نسبت به نظریه معادلات بسیار علاقهمند شد. در سال 1837 مقالهای نوشت تحت عنوان
”ملاحظاتی درباره اینکه یک مسئله هندسی را میتوان با خط کش و پرگار حل کرد.“ که
در نشریه ریاضیات محض و کاربردی لیوویل انتشار یافت. او داستان را از همان
جایی که گاوس رها کرده بود ادامه داد. سرانجام او در سال 1848 در سن 33 سالگی فوت
کرد، و دلیل مرگش نیز احتمالاً کار بیش از حد در زمینه تدریس و مدیریت بوده.

برهان ونتزل
برای ناممکن بودن حل مسئله تثلیث زاویه و تضعیف مکعب، تاحدی شبیه کار حماسی گاوس
در مورد مسئله چندضلعیهای منظم، ولی رویهم رفته از آن خیلی سادهتر بود. من با
مسئله تضعیف مکعب شروع میکنم که موضوع آن خیلی روشن است: آیا میتوان با استفاده
از خطکش و پرگار، خطی را ساخت که طول آن ![]() باشد.
باشد.
تحلیل
گاوس از مسئله چندضلعیهای منظم بر پایه این ایده بنا شده بود که هر نوع ساخت
هندسی، به حل یک سری از معادلات درجه دوم تقلیل پیدا میکند. او تقریباً این را
مسلم میدانست، زیرا ویژگیهای جبری خطوط و دوایر ایجاب میکرد که چنین معادلاتی
برقرار باشد. در جبر بسادگی میتوان ثابت کرد که ”حداقل چندجملهای“ هر کمیت قابل
ساخت (یعنی سادهترین معادلهای که در آن صدق میکند)، درجهای دارد که مساوی یکی
از توانهای عدد 2 است. آن معادله میتواند خطی، درجه 2، 4، 8، 16، 32، 64 و غیره
باشد، ولی هر درجهای که دارد، توانی از 2 است.
از سوی
دیگر، ![]() در
معادله x3-2=0 صدق میکند، و این حداقل چندجملهای برای آن
میباشد، یعنی درجه 3، که توانی از 2 نیست. پس این فرض که میتوان یک مکعب را با
خط کش و پرگار تضعیف کرد، با یک منطق بیعیب و نقص، به این منتهی میشود که پس 3
توانی از 2 است. معلوم است که این درست نیست. درنتیجه بوسیله برهان خلف
میتوان نتیجه گرفت که چنین ساختی نمیتواند وجود داشته باشد.
در
معادله x3-2=0 صدق میکند، و این حداقل چندجملهای برای آن
میباشد، یعنی درجه 3، که توانی از 2 نیست. پس این فرض که میتوان یک مکعب را با
خط کش و پرگار تضعیف کرد، با یک منطق بیعیب و نقص، به این منتهی میشود که پس 3
توانی از 2 است. معلوم است که این درست نیست. درنتیجه بوسیله برهان خلف
میتوان نتیجه گرفت که چنین ساختی نمیتواند وجود داشته باشد.

به دلایل
مشابهی، تثلیث زاویه نیز غیر ممکن است، هر چند اثبات آن کمی طولانیتر است.
اول از
همه باید بگوئیم که میتوان برخی از زوایا را دقیقاً به سه قسمت تقسیم کرد. یک مثال
خوب برای اینمورد زاویه °180
میباشد، که به سه زاویه °60
تقسیم میشود. 60 درجه زاویهای است که ما میتوانیم با کمک یک شش ضلعی منظم
بسازیم، بنابراین اثبات عدمامکان تثلیث زاویه، با انتخاب زوایای دیگری شروع میشود،
و اثبات میگردد که نمیتوان آنرا به سه قسمت تقسیم کرد. سادهترین زاویه از این
دست، خود °60
است. یک سوم این زاویه °20
است، و ما نشان خواهیم داد که °20 را
نمیتوان با استفاده از خطکش و پرگار ساخت.
به مطلبی
که حالا اشاره میکنم دقت کنید زیرا یک ایده کاملاً جِدی است: به نقاله، یا همان
وسیلهای که برای اندازهگیری زوایا از آن استفاده میشود، نگاه کنید. واضح است که
روی آن اعداد °10 و
یا °20 علامت گذاری شده. ولی
این زویا دقیق نیستند (اولین دلیلش هم این است که خطوطی که با آن نقاله مدرج شده
دارای ضخامت میباشند.) ما میتوانیم با استفاده از ابزارهایی نظیر نقاله، برای
کارهایی مثل معماری یا نقشههای مهندسی، زاویههای 20 درجهای تشکیل دهیم که به
اندازه کافی دقیق و قابل قبول باشند، ولی ما نمیتوانیم با استفاده از روشهایی
اقلیدسی زاویه 20
درجهای تشکیل دهیم که کاملاً دقیق باشد (و همین مسئله است که ما میخواهیم آنرا
اثبات کنیم).
کلید
معمای این مسئله، مثلثات (یعنی مطالعه کمّی زوایا) است. فرض کنید که ما کار خود را
با یک شش ضلعی شروع کنیم که در یک دایره با شعاع 1 محاط شده باشد. آنگاه ما براحتی
در آن زاویای °60 را
خواهیم دید، و اگر توانستیم یکی از آنها را به سه قسمت تقسیم کنیم، آنگاه میتوانیم
خط پررنگی را که در شکل نمایش داده شده را بسازیم.
فرض کنید که طول این خط x باشد. مثلثات به ما
میگوید که x
در معادله 8x3- 6x-1=0 صدق میکند.
همانطورر که درمورد مسئله تضعیف مکعب دیدیم، این معادله هم از نوع درجه سوم است، و
این معادله حداقل چندجملهای از x
است. ولی فقط هنگامی میتوان x
را ساخت که درجه چندجملهای آن توانی از 2 باشد. در اینجا باز هم برمیگردیم به
همان مسئله قبل، و باز هم همان استدلال را بکار میبریم: ساخت پارهخط مورد نظر
امکانپذیر نیست.
تثلیث یک زاویه 60 درجهای معادل است با
ساخت یک پاره خط بطول x.
آنگونه که
من این برهانها را ارائه کردم، باعث شد تا ساختار ژفتری از نظر پنهان شود. اگر از
دیدگاه انتزاعیتری نگاه کنیم، خواهیم دید که راه حل ونتزل برای این دو مسئله
باستانی هر دو به بحثهای مربوط به تقارن تقلیل پیدا میکند: گروههای گالوای
معادلات که متناظر با هندسه باشند ساختار نادرستی برای ساخت با خطکش و پرگار
دارند. ونتزل بخوبی از گروههای گالوا آگاه بود، و در سال 1845 برهان جدیدی را
ارائه داد که اثبات میکرد برخی از معادلات جبری را نمیتوان با استفاده از رادیکالها
حل کرد. این برهان به روشهای روفینی و آبل نزدیک بود، ولی نظرات آنها را روشنتر و
آسانتر بیان میکرد. ونتزل در مقدمه این مقاله مینویسد:
”گرچه رویهم
رفته برهان آبل صحیح میباشد، ولی به شکلی ارائه شده که آنقدر آنرا پیچیده و مبهم
میکند که مورد قبول عموم قرار نمیگیرد. سالها قبل، روفینی ... با همین مسئله
مواجه شده بود، آنهم بصورتی که هنوز بسیار مبهمتر از آبل بنظر میرسد... با مطاله
در مورد تحقیقات این دو ریاضیدان ... ما به برهانی رسیدیم که بنظر میرسد آنقدر قوی
باشد که کلیه تردیدها در مورد این قسمت مهم از نظریه معادلات را از میان بردارد.“

تنها مورد
باقیماند از عهد باستان ”مسئله تربیع دایره“ بود، مسئلهای که بر این دلالت دارد
که خطی ساخته شود که طول آن دقیقاً معادل عدد π باشد. معلوم شد که اثبات
غیر ممکن بودن این مورد از موارد دیگر خیلی دشوارتر بود. چرا؟ زیرا بجای
اینکه عدد π دارای حداقل چندجملهای باشد که درجه آن نادرست است، معلوم شد که اصلا
دارای هیچ حداقل چندجملهای نیست. هیچ چند جملهای با ضرائب گویا وجو ندارد که
ریشه آن عدد π باشد. شما میتوانید هرچقدر که دلتان میخواهد به این عدد نزدیک شوید،
ولی نمیتوانید معادلهای را بیابید که ریشه آن دقیقاً برابر π باشد.
ریاضیدانان
قرن نوزدهم متوجه شدند که تمایز بین اعداد گویا و گنگ را باید گستردهتر و دقیقتر
کنند. گونههای مختلفی از اعداد گنگ پیدا شده بود. گونههای ”معمولی“ آنها نظیر ![]() را
نمیتوان دقیقاً بصورت یک عدد کسری بیان کرد (یعنی نسبتی از دو عدد صحیح) ولی
میتوان آنها را با عباراتی که شامل اعداد گویا هستند بیان کرد. مثلاً آنها
میتوانند ریشههای معادلاتی باشند که ضرائب آنها اعداد گویا هستند (در مورد
را
نمیتوان دقیقاً بصورت یک عدد کسری بیان کرد (یعنی نسبتی از دو عدد صحیح) ولی
میتوان آنها را با عباراتی که شامل اعداد گویا هستند بیان کرد. مثلاً آنها
میتوانند ریشههای معادلاتی باشند که ضرائب آنها اعداد گویا هستند (در مورد ![]() این
معادله x2-2=0 است). چنین اعدادی ”اعداد جبری“ نامیده میشوند.
این
معادله x2-2=0 است). چنین اعدادی ”اعداد جبری“ نامیده میشوند.
ولی
ریاضیدانان متوجه شدند که اصولاً ممکن است اعداد گنگی وجود داشته باشند که جبری
نباشند و فاصله آنها با اعداد گنگ معمولی همانقدر باشد که اعداد گویا از اعداد
گنگ. این اعداد روی هم رفته، حوزه اعداد را به مرتبه بالاتری میبردند و به همین
دلیل این اعداد غیرجبری، اعداد عالی، یا ترنسِندنتال[138] نامیده شدند.
...........................................
برای ادامه مطالعه این فصل نسخه
کامل PDF کتاب را تهیه کنید.
ویلیام
روآن همیلتون[148] بزرگترین ریاضیدانی است که تابحال ایرلند به جهان عرضه داشته. او
هنگامی که زنگ ساعت، نیمه شب را اعلام میکرد، در تاریخ 3 یا 4 اگوست 1805 بدنیا
آمد. وی یک زبانشناس برجسته، یک ریاضیدان و یک دائمالخمر بود. او
قصد داشت تا یک جبر سهبعدی را اختراع کند، ولی با جرقهای که ناگهان در ذهنش شکل
گرفت، و باعث شد یک پل را خراب کند، او به جای یک جبر سهبعدی، نوع چهاربعدی آنرا
اختراع کرد، چیزی که نگاه انسان به جبر، فضا، و زمان را برای همیشه تغییر داد.
ویلیام در
یک خانواده متمول بدنیا آمد. او سومین پسر آرچیبالد همیلتون، یک وکیل تاجرمنش بود.
ویلیام خواهری بنام الیزا نیز داشت. پدرش هنگامی که دو یا سه گیلاس مشروب میخورد
سرش گرم میشد، و برای مدتی او را به مصاحب خوبی بدل میکرد، ولی همانطور که از شب
میگذشت و بیشتر مینوشید مایه شرمندگی میشد. آرچیبالد مردی بود که سلیس سخن میگفت،
باهوش و مذهبی بود، و کلیه این صفات خوب را، بهمراه شرابخوارگی، به پسرش جوانش
منتقل کرد. مادر ویلیام، سارا هوتون، که از یک خانواده روشنفکر آمده بود، حتی از
شوهرش هم باهوشتر بود، ولی با سپردن تربیت پسرش در سن سه سالگی به عموی او جیمز،
نفوذش بر روی ویلیام جوان کم شد. جیمز یک کشیش، و همچنین یک زبانشناس قابل
بود، و علایق او بود که به تحصیلات ویلیام جهت داد.
نتایج
آموزشی او تحسین برانگیز بودند. ویلیام تا سن پنج سالگی به زبانهای یونانی، لاتین
و عبری مسلط شده بود. در هشت سالگی او میتوانست فرانسوی و ایتالیایی صحبت کند. دو
سال بعد، او زبانهای عربی و سانسکریت را یادگرفت؛ و بدنبال آن فارسی، سوری، هندو،
مالی، ماهاراتی و بنگالی را به مجموعه زبانهای خود اضافه کرد. تلاشهایی که برای
آموزش زبان چینی به این پسر جوان صورت گرفت، بر اثر کمبود کتابهای مناسب به مانع برخورد
کرد. جیمز از این مسئله شاکی بود و میگفت ”تهیه این کتابها از لندن هزینه زیادی
را روی دست من گذاشته، ولی امیدوارم پول خود را در جای درستی هزینه کرده باشم.“
اریک تمپل
بل[149] ریاضیدان و شبه-مورخ آمریکایی (بدین جهت از
لفظ ”شبه-مورخ“ استفاده میکنم که او در بیشتر مواقع داستانهای خوب را به واقعیات
بد ترجیح میداد.) این سئوال را در مورد همیلتون مطرح میکند و میپرسد ”همه این
آموزشها چه سودی داشت؟“
این از
خوشاقبالی علم و ریاضیات بود که وقتی ویلیام با اعجوبه حساب آمریکایی، زِرا
کولبُرن[150]، آشنا شد از پرداختن بیشتر به زبانشناسی، و
پرکردن ذهنش از هزاران زبان قدیم و جدید دنیا، نجات پیدا کرد! کولبُرن از آن دسته
آدمها بود که بیشتر به یک ماشین حساب جیبی شباهت داشتند؛ او استعداد عجیبی برای محاسبات
سریع و دقیق داست. اگر از او میپرسیدید که ریشه سوم 1,860,867 چیست او بیدرنگ پاسخ میداد ”123“.
به
همانگونه که اگر کسی املاء همه کلمات را بداند لزوماً نویسنده خوبی نخواهد بود،
داشتن چنین استعدادی در محاسبه هم با داشتن قابلیتهای ریاضی متفاوت است. به جز
گاوس که در یادداشتهای و دست نوشتههای خود محاسبات عظیمی را انجام داده،
ریاضیدانان برجسته اندکی بودهاند که حسابکنندههای چالاکی باشند. البته بیشتر
آنها حسابگرهای قابلی بودهاند (در گذشته باید هم اینجور بوده باشد)، ولی با
اینحال به پای یک حسابدار نمیرسیدهاند. حتی امروز هم کامپیوترها جای محاسبات
کاغذی، و یا ذهنی، را بطور کامل پر نکردهاند؛ شما اغلب با انجام محاسبات بصورت
دستی، و نگاه به صورت مسئله، میتوانید نسبت به یک مسئله ریاضی دید خوبی بدست
آورید. ولی با داشتن روشهایی که امروزه توسط ریاضیدانان حرفهای ابداع شده،
هر کسی با یک آموزش یک ساعته میتواند کسانی مانند کولبُرن را شکست دهد.
با اینحال
اگر همه اینکارها را هم انجام دهید باز هم به پای گاوس نمیرسید. قابلیتهای که او
داشت چیز دیگری بود.
کولبُرن
هیچیک از ترفندها و میانبرهایی را که در انجام محاسبات بکار میبرد بطور کامل درک
نمیکرد، هرچند از این مسئله آگاه بود که در این میان حافظه نقش مهمی را ایفا
میکند. او را به همیلتون معرفی نمودند تا بلکه نابغه جوان بتواند آن فنون اسرارآمیز
را درک کند. ویلیام اینکار را انجام داد و حتی آن فنون را بهبود بخشید. زمانی که
کولبرن به کشور خود بازگشت، همیلتون بلاخره چیزی را یافته بود که ارزش آن را داشت
تا قدرت ذهنی خارقالعاده خود را روی آن صرف کند.
تا پیش از
اینکه همیلتون به هفده سالگی برسد، آثار بسیاری از استادان ریاضی را خوانده بود، و
آنقدر ریاضیات نجومی میدانست تا بتواند خورشید گرفتگیها را محاسبه کند. او هنوز
هم وقت خود را بیشتر صرف ادبیات میکرد تا ریاضیات، ولی بزودی این ریاضیات بود که
علاقه واقعی او را تشکیل داد. او خیلی زود شروع به کشفیات جدید کرد. همانطور که
گاوس در 19 سالگی ساخت 17ضلعی منظم را کشف کرد، همیلتون جوان نیز به کشفی نائل آمد
که به همان اندازه مهم محسوب میشد، و آن عبارت بود از نوعی اتحاد (ریاضی) مابین
علم مکانیک و اُپتیک(علم نورشناسی). او ابتدا طی نامهای که به خواهرش الیزا نوشت،
بطور سربستهای به این کشفیات اشاره کرد، ولی با نامههای مکرری که او به پسر عموی
خود آرتور مینویسد، ما میتوانیم بخوبی از ماهیت آنها مطمئن شویم.
این
کشفیات در نوع خود شگفتانگیز بودند. مکانیک علم مطالعه اجسامِ متحرک است؛ مثلاً
گلوله توپی که بصورت سهمی حرکت میکند، پاندولی که بطور منظم از یک سو به سوی دیگر
نوسان میکند، سیاراتی که در مدار بیضی شکل به دور خورشید میچرخند و ... ولی
اُپتیک یعنی مطالعه هندسهِ پرتوهای نور، چیزهایی از قبیل انعکاس و شکست نور، رنگینکمانها،
منشورها، و عدسیهای تلسکوپ. اینکه این دو علم با هم مرتبط بودند جای شگفتی داشت؛
و اینکه این دو یکی هستند واقعاً باورنکردنی بود.
ولی این
واقعیت دارد، و مستقیماً به وضعیتی ختم میشود که امروزه ریاضیدانان و فیزیکریاضیدانان
از آن استفاده میکنند، آنهم نه فقط در مکانیک و اُپتیک، بلکه در نظریه کوانتوم.
به این نوع دستگاهها، به افتخار کاشف آن، دستگاههای همیلتونی[151] میگویند. ویژگی اصلی این دستگاهها این است
که آنها معادلات حرکت دستگاههای مکانیکی را از یک کمیت واحد میگیرند، و آنهم
انرژی کل دستگاه است. این کمیت امروزه ”همیلتونی“ دستگاه نامیده میشوند. معادله
حاصله نه فقط شامل موقعیت اجزاء دستگاه میباشد، بلکه اندازه حرکت آنها (که به
تکانه[152] دستگاه معروف است) را نیز شامل میشود. و بالاخره، این معادلات
ویژگی زیبایی دارند و آن این است که به مختصات خاصی بستگی ندارند. زیبایی واقعیت
است، حداقل در ریاضیات چنین است، و فیزیک این پدیدهها نیز، هم واقعی است و هم
زیبا.

همیلتون
از آبل و گالوا خوششانستر بود، زیرا استعدادهای سرشار او در آغاز کودکی بصورت
گستردهای شناسایی شدند. بنابراین جای تعجب نبود که در سال 1823 در دانشگاه معروف
ایرلند، یعنی کالج ترینیتی دابلین، پذیرفته شود. در کالج ترینیتی او تمام جایزهها
را کسب کرد. از همه مهمتر، در آنجا بود که اولین جلد اثر شاهکارش درباره اُپتیک را
بپایان رساند.
او برای
اولین بار در بهار 1825 جاذبه جنس مخالف را با دختری بنام کاترین دیزنی کشف کرد.
او به طرز غیرعاقلانهای توجه خود را به شعر گفتن منحرف کرد، و آن بهاصطلاح معشوقاش،
فوراً با یک کشیش پولدار که پانزده سال از او مسنتر بود، و از شعر و شاعری هم چیز
زیادی نمیدانست، ازدواج کرد. همیلتون از این مسئله خیلی افسرده شد؛ باوجود اینکه
او مذهبی بار آمده بود، ولی به این فکر افتاده بود تا گناه کبیره مرتکب شده و
خودکشی کند. بالاخره افکار مذهبی بر او چیره شد و باعث شد تا آرامش خود را در شعر
دیگری پیدا کند، و این شعر چیزی نبود جز ریاضیات.
همیلتون
به شعر علاقه داشت، و حلقه دوستان او شامل ادباء زیادی بود. از آن میان، ویلیام
وردزورث[153] یکی از دوستان نزدیک او بود. او همچنین با
نویسندگانی مانند ساموئل تِـیلِر کالریج[154] و دیگران نشست و برخاست داشت. با پندی که
وردرورث به او داد، خدمت ارزشمندی به وی کرد و به ملایمت به او فهماند که استعداد
او در شعر و شاعری نهفته نشده. وردرورث در یکی از نامههای خود به همیلتون مینویسد:
”شما با رگباری از اشعار خود که برایم میفرستید مرا خیلی شادمان میکنید ... ولی
از آن بیم دارم که ممکن است درگیری در اینگونه موضوعات شما را اغوا کرده و از مسیر
دانش منحرف کند ... من به خودم جرات میدهم تا جسارتاً توجه شما را به این مسئله
جلب کنم که آن قسم از کارهای شما در نظم(=شعر) به پای نثرتان نمیرسد ...“
همیلتون
دریافت که شعر حقیقی او ریاضیاتش است، و بطور خردمندانهای توجه خود را به علم معطوف
کرد. در سال 1827، زمانی که هنوز یک دانشجو بود، هنگامی که جان برینکلی از
سمت خود استفا داد تا اسقف شود، او بهاتفاق آرا به سمت استادی ستارهشناسی
دانشگاه ترینیتی برگزیده شد. همیلتون با اشتیاق تمام کار چاپ کتابش در مورد اُپتیک
را شروع کرد. این کتاب اثری کاملاً معتبر برای شتارهشناسان بحساب میآمد، زیرا
طراحی بیشتر ابزارالات نجومی را در برداشت.
ارتباط
کتاب با مکانیک بصورت خیلی ابتدایی مطرح شده بود. تمرکز اصلی کتاب بیشتر بر روی
هندسه پرتوهای نور بود، مثلاً اینکه چگونه وقتی نور بر روی یک آینه بتابند منعکس میشوند،
و یا اینکه وقتی از یک عدسی عبور کنند چطور شکسته میشوند. بعدها معلوم شد نور
خاصیت موجی نیز دارد و ”پرتو نور“ به ”موج نور“ تغییر نام داد. امواج دارای خواص
دیگری، از جمله پراش[155]، هستند. تداخل[156] امواج با یکدیگر اغلب باعث میشود تا لبههای
تصویرِ منعکس شده نرمتر شوند، و حتی باعث میشود تا نور در اطراف گوشهها خمیده
بنظر برسد، خاصیتی که پرتوها نمیتوانند داشته باشند.
هندسه نور
مبحث جدیدی نبود؛ این موضوع بصورت گستردهای توسط ریاضیدانان پیشین مورد مطالعه
قرار گرفته بود، و آغاز آن به فرما، و حتی به فیلسوف یونانی ارسطو بازمیگردد.
کاری که حالا همیلتون برای اُپتیک انجام داد، مانند همان کار معروفی بود که لژاندر
برای مکانیک انجام داد: یعنی رها شدن از هندسه و جانشینی آن با جبر و آنالیز. کار
بخصوصی که وی انجام داد این بود که استدلالات معمول هندسی را، که بر پایه اشکال و
نمودارها قرار داشت، با محاسبات جبری جایگزین کرد.
این یک
پیشرفت عمده بود، زیرا تصاویر غیردقیق را با تحلیلهای قوی جایگزین میکرد. بعدها
ریاضیدانان تلاشهای زیادی کردند تا مسیر همیلتون را برعکس کرده و استدلالات بصری
را دوباره وارد ماجرا کنند. ولی تا آن موقع استدل جبری جزء لاينفک اندیشه ریاضی
شده بود و نوعی همدم طبیعی برای استدلالات واضح بصری بحساب میآمد. در اینجا چرخه
مُد ریاضی هم یک دور کامل زده بود، ولی در سطوحی بالاتر، درست مثل اینکه روی
پیکانی مارپیچی به سمت بالا حرکت کرد.
سهم اصلی
همیلتون در اُپتیک متحد سازی آن شاخه بود. او خیل عظیمی از نتایج را گرفته و همه
آنها را به یک تکنیک اساسی تقلیل داد. مثلاً او بجای دستگاهی از پرتوهای
نور، یک کمیت واحد بنام ”تابع مشخصه[157] دستگاه“ را معرفی کرد. بنابراین هر ترکیب
اُپتیکی توسط یک معادله واحد نشانداده میشد. بعلاوه، این معادله میتوانست
بوسیله روشهای یکسانی حل شود، که منجر به توصیف کامل پرتوهای نور و رفتار آنها میشد.
روشها بر پایه یک اصل کلی قرار گرفته بودند و آن این بود که: پرتوهای نوری
که در هر دستگاه، مثلاً آینه، منشور، و عدسی حرکت میکنند همیشه مسیری را برای
رسیدن به مقصد طی میکنند که زمان کمتری طول بکشد.

فرما
قبلاً حالتهای خاصی از این اصل را کشف کرده بود، و آن را ”اصل کوتاهترین زمان[158]“ مینامید. سادهترین مثال برای توصیف این اصل، انعکاس نور از یک
آینه مسطح است. شکل سمت چپ پرتو نوری را نشان میدهد که از یک نقطه سرچشمه گرفته و
از روی آینه منعکس میشود تا به نقطه دیگری برسد. یکی از اولین اکتشافات در
اُپتیک، قانون انعکاس بود، که میگوید که پرتو وارد شده و پرتو منعکس شده هردو با
سطح آینه زوایای یکسانی را تشکیل میدهند.
فرما فکر جالبی به سرش زد و آن این بود که همانطور
که در شکل سمت راست دیده میشود، قسمت دوم پرتو، و نقطه دوم را در آینه بازتاب
دهد.

چگونه اصل کوتاهترین زمان به قانون انعکاس
منجر میشود
با یاری
گرفتن از قضایای اقلیدس درباره ”دو زاویه مساوی“، میتوانیم بگوئیم در بازتاب نمایش
داده شده، مسیر از نقطه اول به نقطه دوم مسقیم است. ولی اقلیدس ثابت کرد که یک خط
راست کوتاهترین مسیر ممکن بین دو نقطه است، و بدلیل اینکه سرعت نور در هوا ثابت
است، کوتاهترین مسافت با کوتاهترین زمان برابر است. همین قضیه
برای ”از انعکاس درآوردن“ و رسیدن به شکل سمت چپ برقرار است. بنابراین قضیه دو
زوایه مساوی بطور منطقی معادل است با اینکه ”پرتو نور کوتاهترین زمان را در سفر
از نقطه اول به نقطه دوم طی میکند“.
در رابطه
با این موضوع، قانون دیگری که به قانون شکست اسنل[159] معروف است، به ما میگوید که چگونه پرتوهای
نور هنگامی که از هوا وارد آب، یا از هر محیطی وارد محیط دیگری میشوند، دچار
خمیدگی میشوند. با در نظر گرفتن اینکه سرعت نور در آب کندتر از سرعت آن در هوا
است، میتوان با روش مشابهی از آنچه قبلاً شرح داده شد، این قضیه را نتیجه گرفت.
همیلتون یک گام جلوتر رفت و اعلام کرد که اصل حداقل زمان، در مورد کلیه سیستمهای
اُپتیکی کاربرد دارد، و آن فکر را در قالب یک شئ ریاضی، بنام تابع مشخصه، گنجانید.
ریاضیات
گیرا بود، ولی در دستان همیلتون فوراً به نتایج تجربی منجر شد. همیلتون دریافت که
روشهای او حاکی از وجود نوعی ”شکست مخروطی“ هستند، یعنی اگر یک پرتو واحد نور به
یک بلور مناسب برخورد کند، بصورت مخروطی از پرتوها خارج خواهد شد. این پیشبینی که
برای همه کسانی که در شاخه اُپتیک کار میکردند غیرمترقبه بود، و در سال 1832 توسط
هامفری لوید، که از یک بلور معدنی بنام آراگونيت استفاده کرده بود، مورد تائید
قرار گرفت. آن موقع بود که همیلتون یکباره در جامعه علمی به شهرت رسید.
در سال
1832 همیلتون به این فکر افتاد تا سر و سامانی به زندگی خود بدهد، و تصمیم داشت تا
با الِن دو وِر ازدواج کند. او به وردورث گفت که ”افکار این زن را ستایش میکنم.“
بار دیگر شروع به فرستادن اشعار خود برای او کرد، و آماده شده بود تا به او
پیشنهاد ازدواج دهد. ولی در همان هنگام الِن به او گفت که نمیتواند روستای خودش را
ترک کند. همیلتون این را بعنوان یک دست بسر کردن موادبانه تلقی کرد، که درست هم
بود، زیرا سال بعد دختر با کس دیگری ازدواج، و از آنجا هم نقل مکان کرد.
سرانجام
او با هلن بایلی، زن جوانی که در نزدیکی رصدخانه زندگی میکرد، ازدواج کرد.
همیلتون وی را اینچنین توصیف میکند: ”اصلاً باهوش و زرنگ نبود“. ماه عسل آنها
فاجعه بود؛ همیلتون به کارش روی اُپتیک ادامه داد و هلن هم بیمار بود. در سال 1834
آنها صاحب پسری بنام ویلیام ادوین شدند. بعد از آن هلن بیشتر سال را در خانه پدریاش
ماند. پسر دوم آنها، ارچیبالد هنری، در سال 1835 بدنیا آمد، ولی ازدواج آنها درحال
ازهم پاشیدن بود.

آیندگان،
وحدت میکانیکی-اُپتیکی را بزرگترین کشف همیلتون میدانند. ولی چیزی که بیش از همه
فکر او را تا هنگام مرگ بخود مشغول کرده بود، چیزی بود بسیار متفاوتتر: کواترنیونها[160] (=چهارگانها، چهارتاییها).
کواترنیونها
یک ساختار جبری هستند. آنها خیشاوند نزدیک اعداد مختلطند. همیلتون عقیده داشت که
آنها کلید حل ژرفترین مسائل فیزیک هستند؛ بویژه، او در اواخر عمرش براین باور بود
آنها تقریباً کلید همه چیز هستند. ولی بنظر میرسد که تاریخ چنین چیزی را تائید
نکرد، و برای مدت یکصد سال، کواترنیونها کم کم از انظار عمومی فراموش شده و به
مرداب تاریک جبرِ مجرد ریخته شدند، جایی که کاربرد اندکی را میتوان برای آنها تصور
کرد.
ولی در
این آواخر، کواترنیونها دوباره جان تازهای گرفتند. شاید آنها هرگز انتظاراتی که
همیلتون از آنها داشت را برآورده نکرده بودند، ولی بطور فزایندهای بعنوان منبع
مهمی از ساختارهای ریاضی شناخته میشوند. معلوم شده که کواترنیونها جانوران خاصی
هستند، و از این نظر خاص هستند که نیازهای فیزیک مدرن را پاسخ میدهند.
هنگامی که
کواترنیونها برای نخستین بار کشف شدند، انقلاب عمدهای را با خود در جبر به همراه
آوردند. آنها یک قاعده مهم جبری را شکستند. بدنبال آن، در عرض بیست سال، تقریباً
تمام قواعد جبر بصورت عادی شکسته میشد. این روند اغلب با فواید فراوانی همراه
بود، و همانطور بصورت یکسانی به موانع غیرقابل عبوری برخورد میکرد. معلوم شد
مفروضاتی که برای ریاضیدانان ماقبل از 1850 مقدس شمرده میشدند، در حقیقت چیزهای
بودند که فقط کارها را آسانتر میکردند، ولی آنقدرها هم نیاز عمدهای نسبت به آنها
در خود ریاضیات وجود نداشت.
در دوران
بعد از گالوا، که همه جرات و جسارت پیدا کرده بودند، دیگر جبر فقط آن نبود که تنها
از علائم بجای اعداد در معادلات استفاده کند. این علم درباره ساختار درونی معادلات
(یعنی، نه اعداد بلکه روندها)، تبدیلها و تقارنها سخن میگفت. این نوآوریهای
بنیادی چهره ریاضیات را تغییر داد. این دگرگونیها باعث شد تا ریاضیات مجردتر
(انتزاعیتر) شود، ولی درعوض باعث عمومیتر شدن، و قدرتمند شدن، آن نیز گردید. و
کل این مبحث دارای نوعی زیبایی عجیب، و اغلب متحیر کنندهای،
بود.
از زمان
رنسانس، که ریاضیدانان ایتالیا شروع به تفکر در اینباره کردند که آیا جذر 1- معنی
دار هست یا نه، تمام اعدادی که در ریاضیات ظاهر میشدند متعلق به یک دستگاه واحد
بودند. حتی امروز هم پس از گذشت 5 قرن، و بدلیل نوعی شتابزدگی تاریخی، که از رابطه
ریاضیات با واقعیت سرچشمه میگرفت، این دستگاه سنتی به ”دستگاه اعداد حقیقی“
شناخته میشود. این نامگذاری مصیبتبار بوده، زیرا به کسانی که با آن مواجه میشوند
اینطور القاء میکند که انگاری این اعداد به نحوی با تار و پود جهان گره خوردهاند.
خود این دستگاه نیز توسط انسانهایی اختراع شده که میخواستند این جهان را بهتر
بشناسند. این دستگاه (اعداد حقیقی)، حقیقیتر از دیگر دستگاههای جدیدی نیست که در
طول 150 سال اخیر با قوه تخیل انسان اختراع شدهاند. البته اعداد حقیقی، نسبت به بقیه
دستگاهها، رابطه مستقیمتری با واقعیت بیرونی دارند: آنها با شکل اندازهگیری
ایدهآل بستگی خیلی نزدیکی دارند.
یک عدد
حقیقی، اساساً یک عدد اعشاری است. البته نه از این جنبه که آنرا چگونه مثل یک عدد
اعشاری مینویسند، و اینکار موجب راحتتر شدن عملیات حسابی بر روی آنها میشود،
بلکه از جنبه عمیقتری که خواص اعداد اعشاری دارند. اعداد حقیقی از اجداد سادهتری
زاده شدند که نسبت به آنها جاهطلبی کمتری داشتند. در آغاز انسان بطور اتفاقی به
”دستگاه اعداد طبیعی“، (یعنی اعداد 0, 1, 2, 3, و غیر) برخورد کرد.
من از این نظر از لفظ ”برخورد“ استفاده میکنم که در مراحل اولیه، بسیاری از این
چیزهایی که امروزه ما به آنها عدد میگوئیم، اصلاً عدد شمرده نمیشدند. زمانی بود
که یونانیان قدیم از پذیرش 2 بعنوان عدد سرباز میزدند؛ زیرا مقدار آن، آنقدر کم
بود بود که بتواند نمونهای از ”تعدد و تکثر“ باشد، و بهمین دلیل اعداد از 3 شروع
میشدند. سرانجام آنها اجازه دادند که 2 هم مانند بقیه اعداد باشد، ولی با این حال
از قبول 1 سرباز میزدند! اگر کسی پیدا میشد و میگفت ”تعدادی گاو دارد“، و بعداً
معلوم میشد که تنها دارای یک گاو است، به گزافهگویی فراوان محکوم میشد.
مطمعناً منظور از ”عدد“ به معنای ”کثرت“ بود، که باعث میشد ”واحد“ از این جمع حذف
شود.
ولی
همانگونه که دستگاههای عدد نویسی پیشرفت کردند، روشن بود که 1 هم، به اندازه
برادران بزرگتر او، جزیی از دستگاه محاسباتی است. بنابراین 1 هم در شمار اعداد
بحساب آمد (ولی حالت خاصی از آن، عددی بسیار کوچک). از جهاتی این عدد مهمترین عدد
بود، زیرا از همینجا بود که اعداد آغاز میشدند. شما میتوانید با جمع کردن 1ها با
یکدیگر، به هر عددی که خواستید برسید، و زمانی بود که نوشتن اعداد نیز از همین
قاعده پیروی میکرد، مثلاً عدد ”هفت“ را بصورت هفت خط (| | | | | | |) مینوشتند.
به همین
ترتیب، بعدها ریاضیدانان هندی متوجه شدند که عدد مهمتری نیز وجود دارد که قبل از 1
میآید. عدد 1، به هیچ وجه جایی نبود که اعداد از آنجا شروع می شدند. آنها از صفر
شروع میشدند (که حالا ما آن را با علامت 0) نشان میدهیم. بعداً
معلوم شد که مفید است اگر اعداد منفی (اعداد کوچکتر از صفر) را نیز وارد کار کرد.
بنابراین اعداد منفی نیز به دستگاه اعداد پیوستند، و انسان اعداد صحیح را ابداع
کرد: …, -3, -2, -1, 0, 1, 2, 3, … ولی کار به همینجا
متوقف نشد. مشکلی که با اعداد صحیح وجود دارد این است که آنها قادر نیستند بسیاری
از کمیتهای مفید را نشان دهند. برای مثال اگر یک کشاورز بخواهد کمّیتی از گندم را
مشخص کند که مقدار آن بین 1 تا 2 کیسه باشد، نمیتوان آنرا بصورت اعداد صحیح نشان
داد. اگر این مقدار درست در میانه قرار گرفته باشد، آنگاه شامل ![]() 1 کیسه خواهد بود. ممکن
است این مقدار کمتر باشد،
1 کیسه خواهد بود. ممکن
است این مقدار کمتر باشد، ![]() 1، و یا کمی
بیشتر،
1، و یا کمی
بیشتر، ![]() 1. بنابراین کسر اختراع
شد، که بصورتهای مختلفی آنها را نمایش میدادند. کسرها مابین اعداد صحیح جا میگیرند.
همانگونه که در مورد بابلیان باستان دیدیم، کسرهای مرکب هر کمیتی را بخوبی نمایش
میدادند.
1. بنابراین کسر اختراع
شد، که بصورتهای مختلفی آنها را نمایش میدادند. کسرها مابین اعداد صحیح جا میگیرند.
همانگونه که در مورد بابلیان باستان دیدیم، کسرهای مرکب هر کمیتی را بخوبی نمایش
میدادند.
با ورود
فیثاغورس و قضیه معروفش به صحنه، و اینکه برای حساب کردن طول قطر یک مربع واحد
باید عددی را یافت که مربع آن دقیقاً 2 باشد، این مسئله مطرح شد که چنین عددی باید
وجود داشته باشد، زیرا شما میتوانید مربعی رسم کنید، و واضح است که این مربع دارای
قطر است، و این قطر باید دارای طول مشخصی باشد. ولی با کمال تاسف هیپاسوس دریافت
که ریشه دوم عدد 2، هر چه هم که باشد، نمیتواند بصورت یک عدد کسری بیان شود. این
عدد گویا نیست. بنابراین به اعداد بیشتری نیار بود تا این شکاف نامرئی موجود در
کسرها را پُر کند.

سرانجام
بنظر میرسید که این روند به پایان خود رسیده باشد، زیرا یونانیان از الگوهای عددی
دوری کردند تا به الگوهای هندسی بپردازند. ولی در سال 1585، یک ریاضیدان بلژیکی
بنام سیمون استِوین[161]، که در شهر بورگز زندگی میکرد، بوسیله حاکم
آنجا مامور شد تا به پسرش درس بدهد. استِوین بعدها به سمتهای بالاتری از جمله،
بازرس امور آبرسانی، مسئول ارشد تدارکات ارتش، و وزیر امور مالی منصوب شد. این
انتصابات، مخصوصاً دو تای آخر، باعث شد تا او به نوع بهتری از حسابداری نیاز
داشته باشد، و از اینرو، او روش حسابداری ایتالیائیها را اقتباس کرد. او میخواست
دستگاه اعدادی داشته باشد که هم قابلیت انعطاف عدد نویسی هندی-عربی، که از صفر
استفاده میکرد، را داشته باشد، و هم دقت سیستم شصتگانی بابلیها را، که میتوانست
اعداد کسری را با دقت نمایش دهد. راه حل استوین شبیه دستگاه شصتگانی بابلی بود،
منتهی در مبنای ده. این شیوه عدد نویسی، همان دستگاه اعشاری است که ما امروزه از
آن استفاده میکنیم.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
ماریوس
سوفوس لی[180] تنها به این جهت به علم رو آورد که چشمانش ضعیف بود و همین باعث
شد تا از هر گونه شغل نظامی معاف شود. هنگامی که در سال 1865 سوفوس از دانشگاه
کریستینا فارغالتحصیل شد، برخی از درسهای ریاضی، از جمله نظریه گالوا را
گذرانده بود. ولی برای مدتی دودل بود. او میدانست که میخواهد یک شغل دانشگاهی
داشته باشد ولی مطمئن نبود که این شغل باید در زمینه گیاهشناسی، جانورشناسی و یا
نجوم باشد.
مدارکی که
از آن زمان ثبت شده، و در کتابخانه دانشگاه موجود است، نشان میدهند او کمکم به
سمت کتابهای ریاضی رفته، و بیشتر آنها را به امانت گرفته. لی در نیمه یکی از
شبهای1867 ناگهان از خواب پرید، در همین حین، دوستش ارنست موتزفلد نیز از فریادهای
او از خواب بیدار شده. لی فریاد میزده ”من جوابش را پیدا کردم، خیلی ساده است.“
در حقیقت،
چیزی که او یافته بود نگرش جدیدی نسبت به هندسه بود.
لی شروع
به مطالعه آثار هندسهدانان بزرگی همچون جولیوس پلوکر[181] آلمانی، و ژان-ویکتور پونسله[182] فرانسوی نمود. او از پلوکر ایده هندسههایی را گرفت که اجزاء
تشکیل دهنده آن نقطههای مأنوس اقلیدس نبود، بلکه اشیاء دیگری همچون خطوط، صفحات،
و دوایر بود. او در سال 1869 به خرج خودش مقالهای را منتشر کرد و در آن ایده اصلی
خود را مطرح نمود. او نیز مانند آبل و گالوا دریافته بود که ایدههای او برای آن
دوره بیش از حد انقلابی محسوب میشوند، و نشریات عادی نمیخواستند تحقیقات او را
چاپ کنند. ولی ارنست موتزفلد اجازه نداد تا دوستش ناامید شود، و او را تشویق میکرد
تا کارش را بر روی هندسه ادامه دهد. سرانجام یکی از مقالات لی در یکی از نشریات
معتبر چاپ شد و مورد استقبال قرار گرفت. این موضوع باعث شد تا به لی بورسیه تحصیلی
داده شود. حالا او بهاندازه کافی پول داشت تا سفر کند، و به ملاقات ریاضیدانان
برجسته برود و ایدههای خود را با آنها درمیان بگذارد. او به مهد ریاضیات آلمان و
پروس[183]، یعنی گوتینگن و برلین رفت، و با جبردانان معروف لئوپولد کرونکر[184] و ارنست کومر[185]، و همچنین آنالیزدان سرشناس کارل ویرستراس[186] ملاقات کرد. او از روش کار کومر و ویرستراس تحت تاثیر قرار گرفت.
ولی
مهمترین ملاقاتش با فلیکس کلاین[187] در برلین بود. اتفاقاً کلاین شاگرد پلوکر
بود، یعنی همان کسی که لی کتابهایش را مطالعه کرده، و او را میستود و میخواست
دنبالهرو او باشد. لی و کلاین زمینههای مشترکی فراوانی در ریاضیات داشتند، ولی
علایق آنها بطور قابل توجهی با یکدیگر تفاوت میکرد. کلاین جبردانی بود با گرایشهای
هندسی، و دوست داشت بر روی مسائلی کار کند که از یک زیبایی درونی برخوردار باشند؛
لی آنالیزدانی بود که به طیف وسیعی از نظریههای عمومی علاقه داشت. طعنهآمیز است
که این نظریات عمومی لی بود که به ریاضیات مهمترین ساختارهای خاص خود را داد،
ساختارهایی که بعد از گذشت 150 سال از کشف آنها، هنوز هم بطور خیرهکنندهای زیبا
و ژرف هستند، و بیشتر آنها نیز جبری است. اگر شما سعی کنید کلیه اشیاء
ریاضی را درک کنید که از نوع خاصی هستند، بناچار ویژگیهای زیادی را در میان آنها
پیدا خواهید کرد که غیرعادیاند. و اگر بخاطر پافشاری لی بر عمومیت نبود، ممکن بود
این ساختارهای خاص اصلاً کشف نشود.
در سال
1870، لی و کلاین دوباره در پاریس ملاقات کردند، و درآنجا بود که کامیل جُردان[188] توجه لی را به نظریه گروهها جلب کرد. آنروزها گرایش فزایندهای
وجود داشت مبنی بر اینکه هندسه و نظریه گروهها دو سوی یک سکه هستند. ولی زمان
زیادی طول کشید تا این ایده شکل منسجمی بخود بگیرد. در یک همکاری مشترک که بین لی
و کلاین انجام گرفت، آنها سعی کردند بصورت واضحتری رابطه بین هندسه و نظریه گروهها
را مشخص کنند. سرانجام در سال 1872، حاصل این کارها در یک برنامه تحقیقاتی متبلور
شد، و بر اساس آن کلاین کتابی بنام ”برنامه ارلانگن[189]“ منتشر کرد، که مطابق با آن هندسه و نظریه
گروهها باهم یکسان هستند.
امروزه،
این ایده چنان ساده بنظر میرسد که انگار همیشه باید اینطور بوده باشد. گروهی که
متناظر با هر هندسه است، گروه تقارن آن هندسه نامیده میشود. بطور معکوس
نیز، هندسه متناظر با هر گروه، همان چیزی است که گروه تقارن آن است. این یعنی
هندسه بوسیله همان چیزهایی تعریف میشود که در گروه غیرقابل تغییر هستند.
برای مثال
تقارن هندسه اقلیدسی، همان تبدیلاتی در صفحه هستند که طولها، زوایا، خطوط، و
دوایر را بدون تغییر نگاه میدارد. این گروهی است از تمام حرکات صُلب(=ثابت) صفحه،
و از سوی دیگر، هر چیزی که با حرکات صُلب بدون تغییر بماند، بطور طبیعی در قلمرو
هندسه اقلیدسی قرار میگیرد. همین امر بسادگی در مورد هندسههای نااقلیدسی نیز
صادق است، با این تفاوت که در آنها گروههای تبدیل دیگری مطرح است، که پس از اعمال
تبدیل، آن خواصی که در هندسههای مورد نظر مهماند بدون تغییر بمانند.
چرا اصلاً
باید بخودمان زحمت بدهیم تا هندسه را به نظریه گروهها بدل کنیم؟ زیرا این رویکرد
دو راه مختلف را برای شما فراهم میکند تا به هندسه بنگرید، و از طرف دیگر دو راه
مختلف نیز برای فکر کردن درباره گروهها به شما میدهد. برخی اوقات فهم یکی از این
راهها آسانتر است، و برخی اوقات دیگری. ولی بهتر است هر دو آنها یکجا با هم در
نظر گرفته شوند.

روابط بین
فرانسه و پروس بسرعت رو به تیرگی میرفت. امپراطور ناپلئون سوم، پیش خود تصور میکرد
که اگر جنگی را با پروس به راه بیاندازد میتواند محبوبیت روبه زوالش را تحکم
ببخشد. بیسمارک صدراعظم آلمان تلگراف گزندهای برای فرانسویان فرستاد، و جنگهای
فرانسه و پروس در تاریخ 19 جولای 1870 شروع شد. کلاین که یک پروسی بود و در پاریس
زندگی میکرد، محض احتیط به برلین بازگشت.
اما لی یک
نروژی بود و از سفر خود به پاریس نیز بسیار لذت می برد، بنابراین تصمیم گرفت تا در
آنجا بماند. ولی هنگامی که متوجه شد فرانسه در حال شکست خوردن از آلمان است و ارتش
آلمان بسوی مِتز[190] نزدیک میشود، نظرش را تغییر داد. گرچه او
شهروند یک کشور بیطرف بود، اما صلاح نبود تا در یک منطقه بلقوه جنگی بماند.
لی تصمیم
گرفت تا با پای پیاده، و در یک سفر تفریحی، بسوی ایتالیا برود. ولی خیلی دور نرفته
بود که نیروهای فرانسوی او را در حوالی 40 کیلومتری جنوب شرقی پاریس، درحالی
دستگیر کردند که اسنادی را با خود حمل میکرد که حاوی علائم غیر قابل فهمی بودند.
بدلیل اینکه این اسناد سری بنظر میرسیدند، ظاهر امر نشان میداد که لی برای
آلمانها جاسوسی میکند، و به همین دلیل بازداشت شد. دخالت ریاضیدان فرانسوی گاستون
داربو باعث شد که مقامات مسئول متوجه شوند که اینها نوشتهجات ریاضی هستند. لی از
زندان خلاص شد، ارتش فرانسه تسلیم شد، آلمانها پاریس را در محاصره گرفتند، و لی
بار دیگر بسوی ایتالیا حرکت کرد (البته اینبار با موفقیت). او از آنجا به سمت نروژ
حرکت کرد، و در راه بازگشت سری هم به کلاین زد که صحیح و سالم در برلین بود.
لی درسال
1872 دکترای خود را اخذ کرد. جامعه دانشگاهی نروژ چنان تحت تاثیر کارهای او قرار
گرفته بود که در همان سال دانشگاه کریستینا کرسی مخصوصی برای شخص او ایجاد کرد. او
به همراه استاد سابقش لودویگ سیلو، کار ویرایستاری مجموعه آثار آبل را در دست
گرفتند. او در سال 1874 با آنا بریچ ازدواج کرد، و از او صاحب سه فرزند شد.
در این
زمان، لی توجه خود را بر روی موضوع خاصی متمرکز کرد که احساس میکرد بقدر کافی جا
برای گسترش آن هست. در ریاضیات انواع مختلفی از معادلات موجودند، ولی دو نوع آنها
اهمیت ویژهای دارند. یک نوع معادلات جبری هستند، یعنی همانهایی که توسط آبل و
گالوا مورد مطالعه قرار گرفت، و نوع دیگر معادلات دیفرانسیل است، که اولین بار در
کارهای نیوتون در مورد توصیف قوانین فیزیکی مطرح شد. این نوع معادلات دربردارنده
مفاهیمی از حسابان هستند، و بجای اینکه بطور مستقیم با کمیت فیزیکی خاصی سروکار
داشته باشند، آنها نشان میدهند که چگونه آن کمیت با گذشت زمان تغییر میکند. بطور
دقیقتر، آنها آهنگ تغییر کمیتها را مشخص میکنند. برای مثال،
مهمترین قانون حرکت نیوتون حاکی از این است که شتابی که یک جسم میگیرد متناسب است
با برآیند کل نیروهایی که بر آن وارد میشود. شتاب آهنگ تغییر سرعت است، و نه خود
سرعت. قانون حرکت نیوتون بجای اینکه بطور مستقیم به ما بگوید جسم با چه سرعتی در
حال حرکت است، این را مشخص میکند که آهنگ تغییر سرعت آن چقدر است. بطور مشابه،
معادله دیگری که نیوتون آن را برای توصیف تغییر دمای یک شئ در حال سرد شدن بسط
داد، حاکی از آن است که آهنگ تغییر دما متناسب است با تفاوت میان دمای آن
شئ و دمای محیط اطراف آن.
مهمترین
پدیدههای فیزیکی جهان خارج، چیزهایی مثل: حرکت سیالات، کُنشهای گرانشی، حرکت
سیارات، انتقال حرارت، حرکت امواج، کُنشهای مغناطیسی، و انتشار نور و صوت، همگی
آنها با معادلاتی بیان میشوند که از نوع دیفرانسیل هستند. همانطور که نیوتون برای
اولین بار متوجه شد، اگر ما به آهنگ (یا همان نرخ) تغییر کمیتهایی که مشاهده میکنیم
توجه کنیم، و نه به خود کمیتها، آنگاه میتوانیم الگوهای موجود در طبیعت را بهتر و
سادهتر درک کنیم.
لی یک
سئوال مهم را پیش خود مطرح کرد، و آن اینکه آیا یک نظریه کلی برای معادلات
دیفرانسیل، نظیر آنچه گالوا برای معادلات جبری وضع کرد، وجود دارد؟ آیا راهی وجود
دارد تا بتوان مشخص کرد که یک معادله دیفرانسیل را میتوان بوسیله روشهای خاصی حل
کرد؟
بار دیگر،
کلید حل این معما نیز در تقارن نهفته بود. حالا لی متوجه شد که نتایج برخی از
کارهایش در هندسه، میتواند بصورت معادلات دیفرانسیل تفسیر شود. با داشتن جواب یک
معادله مشخص، لی میتوانست تبدیلی را که متعلق به یک گروه خاص است، روی آن اعمال
کند و ثابت کند که نتیجه حاصله نیز یک جواب است. شما میتوانید از یک جواب،
جوابهای بسیاری را حاصل کنید، که همه آنها با گروه رابطه دارند. بعبارت دیگر، گروه
شامل تقارنهای معادله دیفرانسیل میباشد.
این نشانه
واضحی بود از اینکه در پشت این مسائل چیز زیبایی پنهان بود که باید کشف میشد.
کاری که گالوا در مورد وارد کردن تقارن به مبحث معادلات جبری انجام داد را درنظر
بگیرید. حالا تصور کنید که همین کار برای دسته معادلاتی انجام گیرد که خیلی از
انواع جبری مهمتر هستند، یعنی معادلات دیفرانسیل.

گروههایی
که مورد مطالعه گالوا قرار گرفت متناهی و معین هستند. یعنی تعداد تبدیلات یک گروه
یک عدد صحیح معین است. برای مثال، گروه تمام جایگشتهایی که میتواند روی پنج ریشه
یک معادله درجه پنجم انجام گیرد 120 است. ولی برخی از گروههای مهم، از جمله گروههای
تقارن معادلات دیفرانسیل، نامتناهی هستند.
گروه
تقارن یک دایره، نمونهای است از یک گروه نامتناهی ساده، که شامل تبدیلاتی است که
دایره را به هر میزان و به هر شکلی که بچرخانیم، ثابت میمانند. بدلیل اینکه تعداد
بینهایتی از زوایا هستند که میتوان یک دایره را تحت آنها چرخاند، گروه چرخش یک
دایره نامتناهی است. علامتی که این گروه را با نمایش میدهند SO(2) است. در اینجا ”O“ مخفف کلمه ”Orthogonal“، بهمعنای مُتعامد
است، و این یعنی تبدیلات، حرکات صُلب صفحه هستند، و ”S“ مخفف کلمه ”Special“، بهمعنای خاص است،
و این یعنی چرخشها از صفحه خارج نمیشوند.
برای
تقارنهای بازتابی نیز، دایره تعداد بینهایتی محور دارد. اگر شما یک دایره را از
هر قطر آن بازتاب دهید، همان دایره را خواهید گرفت. اضافه کردن بازتابها به گروه
بزرگتری منجر میشود که O(2)
نام دارد.
گروههای SO(2) و O(2) نامتناهی هستند، ولی نامتناهی
بودن آنها منظم است. چرخشهای مختلف با مشخص کردن تنها یک عدد (که همان زاویه
مربوطه باشد) میتوانند تعیین شوند. برای ترکیب دو چرخش با هم، شما کافی است که
زوایای متناظر را با یکدیگر جمع کنید. لی این نوع رفتار را ”پیوسته[191]“ نامید. بنابراین طبق واژگان او، SO(2) یک گروه پیوسته بود. و بدلیل
اینکه تنها یک عدد برای مشخص کردن یک زاویه لازم است، SO(2) یک-بعدی میباشد. همین مسئله
برای O(2)نیز
صادق است. ما نیاز داریم به طریقی بازتاب و چرخش را از یکدیگر متمایز کنیم، و
این هم کاری است که علامت منفی یا مثبت جبری برای ما انجام میدهد.
گروه SO(2) سادهترین مثال از
گروههای لی[192] است، که همزمان دارای
دو ساختار
است: یعنی هم یک گروه است و هم یک مانیفلد[193]. مانیفلد یک فضای چند بعدی است. برای SO(2)، مانیفلد مربوطه یک
دایره است، و عملیات گروه، با جمع کردن زوایای متناظر آنها، دو نقطه روی دایره را
با یکدیگر ترکیب میکند.
دایره
دارای تعداد بینهایتی از تقارنهای چرخشی (شکل سمت چپ) و تعداد بینهایتی تقارنهای
بازتابی (شکل سمت راست) است.
لی یک جنبه بسیار زیبا از این گروهها (گروههای لی)
را کشف کرد، و آن اینکه ساختار این گروها میتواند ”بصورت خطی“ درآورده شود. که
این یعنی، مانیفلد اصلیِ که خمیده است، میتواند با یک فضای اقلیدسی
تخت جایگزین شود. این فضا، فضای مماس بر مانیفلد است. اینمورد برای گروه SO(2) در شکل زیر نشان داده
شده:
از گروه لی تا جبر لی: فضای مماس بر یک
دایره
هنگامی که
ساختار گروه به اینصورت خطی شود، با عث میشود تا فضای مماسی ساختار جبری خاص خود
را بگیرد، که در واقع نسخه ”بینهایت کوچک شده“ ساختار گروه است. این جبر لی[194] آن گروه نامیده میشود، و همان بعدی را دارد
که گروه مربوطه دارا است، ولی بدلیل اینکه هندسه آن تخت است، خیلی سادهتر میباشد.
البته
برای این سادگی باید بهایی هم پرداخته شود: جبر لی مهمترین خواص گروه متناظر خود
را دربر دارد، ولی برخی جزئیات ظریف از آن حذف شدهاند، و آن خواصی هم که
باقیمانده، دستخوش برخی تغییرات جزئی قرار گرفته. با اینحال، شما میتوانید با
بررسی ”جبر لی“ یک گروه، چیزهای زیادی را درباره ”گروه لی“ آن فرا بگیرید، و
پاسخ بسیاری از سئوالات را میتوان بصورت آسانتری در ”جبر لی“ جستجو کرد تا در
”گروه لی“.
معلوم شد
که یکی از مهمترین بصیرتهایی که لی از خود نشان داد این بود که مشخص کند طبیعیترین
عمل جبری روی جبر لی حاصل ضرب AB
نیست، بلکه تفاوت AB - BA
است، که جابجاگر[195] نامیده میشود. برای گروههایی مثل SO(2) که در آن AB = BA، جابجاگر صفر است. ولی در گروههایی نظیر SO(3)، یا همان گروه چرخش
در فضای سه بعدی، AB - BA صفر نیست مگر آنکه محور چرخش A
و B
یا برهم عمود، و یا برهم منطبق باشند. بنابراین هندسه گروه، رفتار جابجاگرها را
نشان میدهد.
سرانجام
با بوجود آمدن نظریه ”میدانهای دیفرانسیل“ در اوایل قرن بیستم، رویای لی برای داشتن
نوعی از ”گروه گالوا“ برای معادلات دیفرانسیل به تحقق پیوست. ولی معلوم شد که
نظریه گروههای لی خیلی مهمتر، و بصورت گستردهای تواناتر از آن هستند که لی
انتظار داشت. نظریه گروههای لی و جبرهای لی بجای اینکه فقط ابزاری باشند برای
تعیین اینکه آیا یک معادله دیفرانسیل را میتوان با روش بخصوصی حل کرد، چنان در
شاخههای مختلف ریاضیات نفوذ کردند که نظیر آن کمتر دیده شده بود. ”نظریه لی“
فراتر از لی رفت و به چیزی مبدل شد که حتی خالق آن هم تصورش را نمیکرد.
اگر خوب
دقت کنیم خواهیم دید که دلیل همه اینها تقارن است. تقارن عمیقاً در تمام حوزههای
ریاضی نفوذ کرده، و اساسیترین ایدههای فیزیک ریاضی بر پایه آن قرار دارند. تقارن
توصیف کننده نظم حاکم بر جهان است، و همین نظم است که فیزیک را به پیش میبرد.
تقارنهای پیوستهای همچون چرخش، بطور نزدیکی با ماهیت فضا، زمان، و ماده رابطه
دارند؛ آنها بر انواع مختلف قوانین بقاء دلالت دارند، از جمله قانون بقای انرژی،
که میگوید هر سیستم بستهای نه میتواند انرژی بگیرد و نه میتواند انرژی از دست
بدهد. این ارتباط بوسیله امی نوتر[196]، که یکی از شاگردان هیلبرت بود، کشف شد.
البته،
مانند همان کاری که گالوا و رهروانش انجام دادند، و بسیاری از خواص گروههای
متناهی را مشخص کردند، گام بعدی در این راه نیز این بود که تمام گروههای لیِ ممکن
شناخته شود. اینجا بود که ریاضیدان دیگری وارد صحنه میشود.
آنا
کاترینا خیلی نگران پسرش بود. دکتر به او گفته بود که پسر جوانش ویلهلم ”خیلی ضعیف
و درعین حال دست و پا چلفتی، و همیشه هم هیجان زده است. ولی ضمناً او بطور عجیبی
عاشق کتاب خواندن هم هست.“ همانطور که ویلهلم بزرگتر میشد، سلامتی او نیز بهبود
مییافت، ولی عشقش به کتاب خواندن کاسته نمیشد. درست قبل از تولد 39 سالگیاش، او
یک مقاله تحقیقاتی ریاضی را منتشر کرد، که بحق از آن بعنوان ”بزرگترین مقاله
ریاضی تمام اعصار“ یاد میشود. البته چنین توصیفاتی به نظر شخصی گوینده آن بستگی
دارند، ولی مطمئناً مقالهای که ویلهلم منتشر کرد در فهرست بهترینها قرار میگیرد.
ویلهلم کارل
کیلینگ[197] فرزند جوزف کیلینگ و آنا کاترینا کورترنباخ بود. او یک برادر و
یک خواهر نیز داشت. پدرش کارمند حقوقی، و مادرش دختر یک داروساز بود. آنها در
بورباخ، شهری در نواحی شرقی آلمان مرکزی، ازدواج کردند، و خیلی زود به مدباخ نقل
مکان کردند، جایی که جوزف شهردار آنجا شد. پس از آن شهردار وینتربرگ، و بعد از آن
شهردار روتن گردید.
خانواده
آنها در رفاه بسر میبرد و استطاعت آن را داشتند تا برای آماده کردن ویلهلم برای
ورود به دبیرستان معلم خصوصی بگیرند. او در دبیرستان به ادبیات کلاسیک، از جمله
لاتین، عبری، و یونانی علاقه داشت. معلمی بنام هارنیشماخر او را با ریاضیات آشنا
کرد؛ ویلهلم در هندسه خیلی خوب بود، و تصمیم گرفت تا ریاضیدان شود. او به دانشگاه
مونستر، که در آن موقع تنها یک آکادمی سلطنتی بود، رفت. آن آکادمی کلاسهای ریاضیات
پیشرفته نداشت، بنابراین کیلینگ خودش به خودش آموزش داد. او آثار هندسی پلوکر را
خواند و سعی کرد تا قضایای جدیدی را از آنها نتیجه بگیرد. او همچنین کتاب تحقیقات
حسابی گاوس را نیز مطالعه کرد.
پس از دو
سال که در آکادمی بود به برلین نقل مکان کرد، جایی که در آن کیفیت آموزش ریاضی
بسیار بالاتر بود، و تحت تاثیر ریاضیدانانی چون ویرستراس، کومر، و هرمن فون هلمهولتز[198] قرار گرفت. هلمهولتز فیزیکریاضیدانی بود که رابطه بین بقا انرژی
و تقارن را روشن کرد. کیلینگ تز دکترایش را، که بر پایه برخی از ایدههای ویرستراس
قرار داشت، در رابطه با هندسه سطوح نوشت، و بعنوان معلم ریاضی و فیزیک شغلی برای
خود دست و پا کرد.
در سال
1875 او با دختر یک معلم موسیقی، بنام آنا کومر ازدواج کرد. دو فرزند اول آنها در
ابتدای طفولیت تلف شدند. پس از آن صاحب دو دختر بنامهای ماریا و آنا شدند و بعد از
آن کیلینگ صاحب دو پسر نیز شد.
در سال
1878 او به مدرسه قدیمی خود بازگشت ، ولی حالا معلم آنجا بود. مشغله وی زیاد بود،
حدود 36 ساعت درس در هفته، ولی با اینحال او وقت کافی برای ادامه تحقیقات ریاضی
خود پیدا میکرد (این کاریست که همیشه بزرگان انجام میدهند). او مقالات مهمی در
نشریات معتبر آن روز منتشر کرد.
در سال
1882 ویرستراس برای کیلینگ شغل استادی دانشگاه بروانسبرگ را پیدا کرد، که وی ده
سال را در آنجا سپری کرد. دانشگاه بروانسبرگ سُنت ریاضی قوی نداشت و به استادان
خود بورسیه تحقیقاتی نمیداد، ولی بنظر میرسید که کیلینگ به چنین انگیزههایی
نیاز نداشته باشد، زیرا در همانجا بود که او به یکی از مهمترین کشفیات در تاریخ
ریاضیات دست یافت، کشفی که بیش از اینکه او را خوشحال کند، وی را ناامید کرد.
چیزی که
او امید داشت بدست آورد بسیار جاهطلبانه بود. او میخواست ”تمام گروههای لی
ممکن“ را تشریح کند. دانشگاه بروانسبرگ نشریههایی که مقالات لی
در آن چاپ میشد را نمیخرید، و کیلینگ از کارهای لی اطلاع زیادی نداشت، ولی با
اینحال در سال 1884 نقشی را که جبرهای لی میتوانند داشته باشند را بطور مستقل کشف
کرد. بنابراین کلیلنگ میدانست که هر گروه لی با یک جبر لی وابسته است، و سریعاً
دریافت که محتملاً جبرهای لی میتوانند خیلی مهار شدنیتر از گروههای لی باشند.
بنابراین مشکل او به این تقلیل یافت که ”تمام جبرهای لی ممکن“ را طبقه بندی کند.
معلوم شد
که این مسئله بسیار دشوار است. امروزه ما میدانیم که این مسئله احتمالاً جواب
معقولی ندارد، زیرا هیچ راه سادی وجود ندارد که با آن بتوان، طی یک روند یکنواخت و
شفاف، تمام جبرهای لی را تولید کرد. بنابراین کیلینگ مجبور شد به چیز بسیار
آسانتری بسنده کند، و آنهم این بود که سازههای اصلی که تمام جبرهای لی از آنها
شکل میگیرد را تشریح کند. این شبیه این است که بخواهیم کلیه سبکهای معماری ممکن
را تشریح کنیم، ولی نهایتاً مجبور شویم به فهرستی از شکل و اندازه آجرها قناعت
کنیم.
این سازههای
اصلی، به جبرهای ساده لی معروف هستند. به همان صورتی که گالوا گروههای
ساده را مشخص کرد (یعنی گروههایی که هیچ زیرگروه نرمالی جز زیرگروههای بدیهی خود
ندارد)، جبرهای ساده لی نیز با خواص مشابهی مشخص میشوند. در واقع، یک گروه ساده
لی دارای یک جبر ساده لی است، و عکس آن نیز تااندازه بسیار زیادی صادق است. کیلینگ
بطور شگفتآوری موفق شد تا تمام جبرهای ساده لی که ممکن بود وجود داشته باشند را
فهرست کند. ریاضیدانان به چنین قضیهای ”طبقهبندی[199]“ میگویند.
از نگاه
کیلینگ این طبقهبندی، نسخه بسیار محدود شده چیزی عامتر بود. اگر او میخواست
دراین راه بجایی برسد باید چندین فرض را مسلم میگرفت، و همین باعث ناامیدی او شد.
بویژه، او از اینکه میدید باید فرض را بر سادگی بگذارد خسته شده بود. بخاطر همین
بود که او مجبور شد بجای اینکه جبرهای لی را در حوزه اعداد حقیقی مطالعه کند، آنها
را روی اعداد مختلط مطالعه کرد. اعداد مختلط رفتار بهتری دارند ولی درعوض با مسائل
هندسی که کیلینگ به آنها اشتیاق داشت، ارتباط مستقیم کمتری داشتند. بدلیل محدودیتهای
خود خواسته، کیلینگ نمیخواست کارهایش را منتشر کند.
او تصمیم
گرفت تا با لی تماس برقرار کند. در ابتدا تماسهای وی بیثمر بود، و خواست از طریق
کلاین با لی ارتباط برقرار کند. کلاین او را به دستیار لی، فردریک انگل، که آن
موقع در دانشگاه کریستینا کار میکرد، معرفی کرد. کیلینگ و انگل باهم جور شدند، و
انگل یکی از طرفدان پر و پا قرص کارهای کیلینگ شد، و به وی کمک کرد تا برخی از
موانع را پشت سر بگذارد، و او را تشویق کرد تا ایده های خود را گسترش دهد. اگر کمک
انگل نبود ممکن بود کیلینگ دست از تلاش بکشد.
در اوایل
کار، کیلینگ تصور میکرد که تمام جبرهای ساده لی را میشناسد، و اینها هم عبارتند
از جبرهای لی so(n)
و su(n)
که متناظر هستند با دو دسته نامتناهی از گروههای کلی، یعنی گروه متعامد خاص SO(n) که شامل تمام چرخشها
در فضای n-بعدی بود، و مشابه آنها گروههای یکانی خاص
، یا SU(n)،
که در فضای n-بعدی مختلط بود.
در
تابستان سال 1886 کیلینگ به دیدن لی و انگل آمد، و آنها را در لیپزیک، جایی که هر
دو آنها کار میکردند، ملاقات کرد. متاسفانه بین لی و کیلینگ برخوردهایی روی داد؛
لی هرگز از کارهای کیلینگ بطور جدی قدردانی نکرد و بیشتر سعی کرد تا از اهمیت
کارهای او بکاهد.

...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
در
آغاز قرن بیستم، گروهها به فیزیک ذرات بنیادی نیز رخنه کردند، و این حوزه از علم
را به همان اندازه متحول کردند که خود ریاضیات را.
در سال
طلائی 1905، مردی که بعدها برجستهترین دانشند زمان خود شد، سه مقاله منتشر کرد که
هر یک از آنها شاخههای مختلفی از فیزیک را دگرگون کرد. او در آن زمان یک دانشمند
حرفهای نبود، و با اینکه از دانشگاه فارغالتحصیل شده بود، هنوز نتوانسته بود یک
شغل معلمی برای خود بدست آورد، و بهمین دلیل بعنوان کارمند دفتر ثبت اختراعات در
برن سویس کار میکرد. و البته، همانطور که اکثراً میدانند، نام او آلبرت اینشتین
است.
اگر کسی
باشد که نام او مترادف با فیزیک نوین باشد، این شخص کسی نیست جزء اینشتین. در نظر
بسیاری او یک نابغه ریاضی هم محسوب میشد، ولی حقیقت این است که او آنقدرها هم
ریاضیدان قابلی نبود، حداقل در ضمینه ریاضی آنقدر خلاق نبود که بتوان او را با
کسانی همچون گالوا و کیلینگ مقایسه کرد. خلاقیت اینشتین در بوجود آوردن ایدههای
نوین ریاضی نبود، بلکه بینش فوقالعاده قوی بود که نسبت به جهان فیزیکی داشت،
بینشی که بخوبی قادر بود آنرا با ریاضیات تشریح کند. اینشتین همچنین استعدادی خوبی
برای تشخیص دیدگاههای مناسب فلسفی داشت. او از میان سادهترین اصول، نظریاتی را
استنتاج میکرد که بنیادی بودند، و الهامبخش او بیشتر نوعی حس زیبایی بود تا
حقایق تجربی. او اعتقاد داشت که نگرشهای مهم همیشه میتوانند به تعدادی اصول کلیدی
تقسیم شوند. در نظر او نیز، واقعیت جهان در زیبایی آن بود.
هزاران
مقاله تحقیقاتی، و تعداد بیشماری کتاب درباره زندگی و کارهای اینشتین چاپ
شده، که نمیتوان هیچ یک را بر دیگری ترجیح داد. ولی چیزی که از نظر ما اهمیت دارد
این است که او نقشی کلیدی در تاریخ تقارن ایفا کرد: این اینشتین بود که بیش از هر
کس دیگری موجب شد تا تقارن ریاضی در فیزیک بنیادی وارد شود. البته من فکر نمیکنم
خود اینشتین چنین دیدی داشت: از نظر او، ریاضیات خادم فیزیک بود، خادمی که اغلب
نافرمان بود. یک نسل طول کشید تا پرده از زیبایی و عمق مفاهیمی که کارهای او بر
اساس آنها قرار گرفته بود برداشته شود.
بنابراین
ما مجبوریم رئوس حوادث زندگی این کارمند ثبت اختراعات را مروری دوباره کنیم تا
ببینیم او چگونه بشهرت رسید. بدلیل اینکه او تنها یکی از افرادی است که در داستان
ما سهم دارد، من تنها به وقایعی میپردازم که به موضوع مورد بحث ما مربوط میشوند.
اگر شما کتاب کامل و بیطرفی درباره زندگی حرفهای اینشتین میخواهید، باید کتاب
آبراهام پایس بنام ” خدا محیل است[205]“ را مطالعه کنید. عنوان این کتاب از یکی از
جملات قصار اینشتین الهام گرفته که یکبار گفته بود ” خدا محیل است، ولی بدجنس
نیست.“
اینشتین،
که علاقه اندکی به دین داشت، زندگی خود را وقف این اصل کرد که جهان قابل فهم است و
بر پایه اصول ریاضی کار میکند. او در بسیاری از کلمات قصارش به خدا توسل میکرد،
ولی نه بعنوان موجودی ماورالطبيعه که به زندگی خصوصی انسانها علاقه دارد، بلکه خدا
را همچون نشانی از نظم و ترتیب جهان میدانست. او هیچ خدایی را نمیپرستید و مراسم
مذهبی هیچ دینی را بجا نمیآورد.

عموماً از
اینشتین بعنوان جانشین بحق نیوتون نام برده میشود. عنوان اصلی کتاب مهم نیوتون
”اصول ریاضی فلسفه طبیعی[206]“ بود، که در زیر آن، عنوان فرعی ”نظام جهان“
به چشم میخورد. دانشمندان بسیاری پس از نیوتون ظهور کردند که دیدگاه ما را نسبت
به ”نظام جهان“ غنیتر کردند، ولی اینشتین اولین کسی بود که تغییرات عمدهای در
این دیدگاه ایجاد کرد. پیش از اینشتین، مهمترین نظریهپرداز جیمز کلرک ماکسول[207] بود که معادلاتش در زمینه الکترومغناطیس، پدیدههای الکتریکی و
مغناطیسی، و بویژه نور، را در حوزه فیزیک نیوتونی قرار داد. اینشتین از این خیلی
فراتر رفت، و موجب شد تا تغییرات عمدهای بوجود آید. بطور طعنهآمیزی، تغییراتی که
منجر به بازبینی نظریه گرانش شدند، پیامد نظریه امواج الکترومغناطیسی بودند. حتی
طعنهآمیزتر اینکه، برخلاف نظر نیوتون که عقیده داشت نور یک پدیده موجی نیست، یک
وجه اساسی این نظریه موجی بودن نور است که در آن نقش محوری دارد. کلام آخر اینکه
یکی از زیباترین آزمایشاتی که امروزه انجام میشود تا نشان دهد نور یک پدیده
موجی است، اولین بار توسط خود نیوتون انجام گرفت، که خودش اعتقادی به موجی
بودن نور نداشت.
علاقه
انسان به مبحث نور دست کم به زمان ارسطو بازمیگردد. ارسطو فیلسوفی بود که
سئوالاتی را مطرح میکرد که بیشتر جنبه علمی داشتند، مثلاً اینکه ما چگونه میبینیم؟
ارسطو عقیده داشت که وقتی ما به یک شئ نگاه میکنیم، رسانهای که بین آن شئ و چشم ناظر
قرار دارد ( و حالا ما به آن ”هوا“ میگوییم)، تحت تائیر شئ قرار میگیرد و
تغییراتی در آن بوجود میآید. سپس چشم به تغییرات پیش آمده در رسانه پیمیبرد، و
نتیجه کار حس بینایی است.
در قرون
وسطا این طرز تلقی برعکس شد. در آن موقع اینطور تصور میشد که چشمان ما نوعی پرتو
از خودش ساطع میکند، که هر چیزی را که ما به آن نگاه میکنیم روشن میکند. بعبارت
دیگر، در عوض اینکه اشیاء از خود علائمی را بسوی چشم ما بفرستند، چشم ما بود که بر
تمام اشیاء رد-چشم میگذاشت.
سرانجام
معلوم شد که ما اشیاء را توسط نوری که از آنها منعکس میشود میبینیم، و در زندگی
روزانه ما، منبع اصلی نوری که از روی اشیاء منعکس میشود خورشید است. آزمایشات
نشان میدهند که نور به خط مستقیم حرکت میکند، و ”پرتوها“ را شکل میدهد. بازتاب (
یا انعکاس) هنگامی روی میدهد که یک پرتو نور از روی یک سطح برگشت کند. بنابراین
وقتی خورشید از خودش پرتوهای نوری ساطع کند، و آنها در سر راه خود به چیزهایی
برخورد کنند، این پرتوها از روی آنها بازمیگردند و برخی از آنها وارد چشم ناظر میشود،
چشم علائمی را که دریافت کرده پردازش میکند، و این باعث میشود که ما آن چیزهایی
را ببینیم که از خود نور میتابانند.
سئوال
اصلی این بود که نور چیست؟ نور کارهای حیرتانگیزی میکند. نه فقط بازتاب، بلکه
شکست نیز دارد. شکست نور پدیدهای است که از تغییر ناگهانی مسیر نور، هنگامی که از
یک محط به محیط دیگر وارد میشود، بوجود میآید. این همان پدیدهای است که موجب میشود
تا وقتی یک چوب را در حوز آب فرو میکنیم، خمیده بنظر بیاید، و همین پدیده است که
موجب عملکرد عدسیها میشود.
حتی پدیدهای
وجود دارد که از اینها نیز حیرتانگیزتر است و پراش نور نامیده میشود. در سال
1664، دانشمند و عالم انگلیسی، رابرت هوک[208]، که اغلب با نیوتون در جدال بود، کشف کرد که
اگر یک عدسی را در بالای یک آینه تخت قرار دهد و از داخل عدسی نگاه کند، حلقههای
رنگی هممرکزی ظاهر میشوند. بدلیل اینکه نیوتون اولین کسی بود که تشکیل این حلقهها
را تحلیل کرد، حالا اینها ”حلقههای نیوتون“ نامیده میشوند. امروزه ما این آزمایش
را دلیل روشنی برای موجی بودن نور بحساب میآوریم، زیرا این حلقهها لبههای تداخل
امواج هستند، جایی که در آن امواج یا یکدیگر را تقویت، و یا حذف، میکنند. ولی
نیوتون باور نداشت که نور یک پدیده موجی است. او عقیده داشت بدلیل اینکه نور بصورت
مستقیم حرکت میکند، بنابراین باید نوعی از حرکت ذرات باشد. او در کتاب ”اُپتیک“
خود مینویسد ”نور از ذرات ریزی بنام کورپُسِل[209] تشکیل شده که توسط اجسام نورانی گسیل میشوند.“
نظریه ذرهای نور میتوانست به آسانی پدیده انعکاس را توضیح دهد، به این صورت که
ذرات هنگامی که به یک سطح برخورد میکنند از روی آن به سوی دیگری پرتاب میشوند.
اما این نظریه در توضیح پدیده شکست نور با دشواری مواجه میشد، و برای پدیده پراش
نور هم کلاً هیچ توضیحی نداشت.
نیوتون با
تفکر بر روی دلیل شکست پرتوهای نور به این نتیجه رسید که ریشه این مسئله باید در
محیط انتشار نور باشد، و نه خود نور. این باعث شد تا او این نظر را مطرح کند که یک
”رسانه ناپیدایی“ بنام ایثر[210] وجود دارد که ارتعاشات را سریعتر از نور منتشر
میکند. او به این نتیجه رسیده بود که تشعشع گرمایی دلیلی بر وجود این ارتعاشات
بود، زیرا میدید تابش گرما میتواند در خلاء نیز حرکت کند. بر همین اساس، باید
چیزی در خلاء وجود داشته باشد تا گرما را با خود حمل کند، و موجب شکست و پراش نور
شود. به گفته نیوتون:
”آیا
گرمای اتاق توسط ارتعاش رسانهای که از هوا خیلی رقیقتر است، از میان خلاء عبور
نمیکند؟ رسانهای که وقتی هوا را از محیط خارج میکنیم باز هم در آن وجود دارد. و
آیا این همان رسانه نیست که نور در آن انعکاس و انکسار (شکست) پیدا میکند؟“
هنگامی که
من این جملات را میخواندم بیاختیار سخنان دوست خودم، تِری پراچت[211]، را بیاد میآوردم که کتابهای تخیلی او بنام ”جهانِگردون[212]“ جهان واقعی ما را به سخره میگیرد، جهانی که در آن ساحران، افسونگران،
اجنه، و کوتولهها بر روی نقاط ضعف انسانها دست میگزارند و آنها را مسخره میکنند.
در ”جهانِگردون“، سرعت نور تقریباً بهاندازه صوت است، و به همین دلیل است
که نور سپیده دم را درحالی که به مزرعه نزدیک میشود میتوان مشاهده کرد. تاریکی
همدم لازم نور است (در جهان گردون تقریباً همه چیزها حالتی عینی بخود میگیرند)
و ظاهراً تاریکی سریعتر از نور حرکت میکند زیرا باید از سر راه نور بگریزد. گذشته
از این واقعیت ناامید کننده که هیچ یک از اینها درست نیست، ولی حتی در جهان ما نیز
چنین چیزهای قابل لمس بنظر میرسند.
نظریه
نیوتون درباره نور نیز از همین نقیصه رنج میبرد. نیوتون شخص نادانی نبود، و بنظر
میرسید که نظریه او به برخی از سئوالات مهم پاسخ میدهد. متاسفانه این پاسخها بر
پایه یک سوءبرداشت بنا شده بودند: او تصور میکرد که تشعشع گرما و نور دو چیز
متفاوت هستند. او تصور میکرد که وقتی نور به سطحی برخورد میکند، موجب برانگیخته
شدن ارتعاشات گرمائی میشود، و انواع مختلف همین ارتعاشات است که موجب میشود تا
نور منعکس، و یا شکسته، شود.
از همینجا
بود که مفهوم ”ایثر تابناک[213]“ پدید آمد. بویژه هنگامی که معلوم شد نور یک
پدیده موجی است، این ایثر حکم رسانهای را داشت که نور در آن موج میزند. (امروزه
تصور ما برا این است که نور نه یک پدیده کاملاً موجی، و نه کاملاً ذرهای است،
بلکه ترکیبی از هر دو آنهاست، چیزی که میتوان به آن موجزره گفت. ولی فعلاً برای
توضیح آن کمی زود است.)
ولی با همه اینها، این ایثر چه بود؟ نیوتون در این باره
کاملاً صادق است و میگوید ”من
نمیدانم ایثر چیست.“ او استدلال میکند که اگر ایثر از ذره تشکیل شده باشد، آنگاه
این ذرات باید از ذرات هوا، و حتی از ذرات نور، خیلی کوچکتر باشند، و اگر بخواهیم
به زبان جهانِ گردون سخن بگوییم، آنها باید قادر باشند از سر راه نور کنار بروند.
نیوتون درباره ایثر چنین میگوید ”کوچکی فوقالعاده ذرات ایثر ممکن است در اثر
بزرگی نیروهایی باشد که توسط دیگر ذرات مشابه به آنها وارد میشود، و موجب میشود
چنین رسانهای آنقدر رقیق باشد که از هوا کشسانتر است، و درنتیجه تاحد زیادی در
برابر حرکات پرتابهای قادر به مقاومت نیست.“
پیش از
نیوتون، فیزیکدان هلندی کریستیان هویگنس[214]، در کتاب خود بنام ”مقالاتی در باره نور“ که
در 1678 منتشر شد، نظریه دیگری درباره نور مطرح میکند. او در آنجا میگوید نور یک
پدیده موجی است. این نظریه میتوانست پدیدههایی نظیر بازتاب، شکست، و همچین پراش
نور را بصورت شسته-رفتهای توضیح دهد. برای مثال، اثرات مشابه این را میتوان در
امواج آب مشاهده کرد. اینجا ایثر همان نقشی را برای نور دارد که آب برای امواج
اقیانوس دارند (یعنی همان چیزی که به هنگام گذر امواج به حرکت درمیآید.) ولی
نیوتون با این مسئله موافق نبود. این بحث حالت گیج کنندهای بخود گرفت، زیرا هر دو
دانشمند فرضیات نادرستی درباره ماهیت این امواج درنظر داشتند.
همه چیز
با وارد شدن ماکسول تغییر کرد. او نیز بر روی شانههای غول دیگری ایستاده بود.

بخاری
برقی، رعد و برق، رادیو، تلویزیون، غذاسازها، اجاقهای مایکروویو، یخچالها، جارو
برقیها، و تعداد بیشماری از وسایل صنعتی دیگر، همگی از بصیرت یک مرد نشأت گرفته،
مایکل فارادی[215]. فارادی در سال 1791 در لندن بدنیا آمد. او فرزند یک آهنگر بود که
در دوران ملکه ویکتوریا به درجات عالی علمی صعود کرد. پدرش به یک فرقه کوچک مسحی
بنام ساندمانیان[216] تعلق داشت.
فارادی در
1805 شاگرد یک صحاف کتاب شد و از همان موقع آزمایشهای علمی خود، بویژه در شیمی،
را شروع کرد. درسال 1810 او عضو انجمن فلسفی شهر شد. این انجمن متشکل بود از مردان
جوانی که برای بحث و گفتگو در باره موضوعات علمی دور یکدیگر جمع میشدند، و این
مورد باعث شد تا علاقه فارادی به علم شدت گیرد. در سال 1812 او اجازه یافت که در
درسهای نهایی، سر هامفری دیوی[217]، که در آن موقع بزرگترین شیمیدان انگلستان
بود، شرکت کند. مدت کوتاهی پس از آن، فارادی از دیوی درخواست کرد که شغلی به بدهد،
به همین جهت با او مصاحبهای صورت گرفت، ولی هیچ منصب خالی برای او وجود نداشت.
ولی پس از اینکه دستیار فارادی بدلیل براه انداختن یک دعوا اخراج شد، فارادی جای
او را گرفت.
از سال
1813 تا 1815، فارادی به همراه دیوی و همسرش، اروپا را گشتند. ناپلئون برای ادامه
سفر دیوی در سرزمینهای که تحت سلطه فرانسه قرار داشت به او یک گذرنامه داد که به
وی اجازه میداد یک ملازم نیز همراه خود داشته باشد. جین، همسر دیوی، بصورت ظاهری
عنوان ملازم را برای خود برداشته بود. فارادی از اینکه میدید جین از او انتظار
دارد تا مانند پیشخدمت او باشد بشدت آزرده خاطر بود. در سال 1821 حوادث بصورتی رقم
خورد که به نفع فارادی بود: او ترفیع گرفت و با سارا بارنارد، دختر یک ساندمانیان
سرشناس ازدواج کرد. از آن بهتر، تحقیقات او در زمینه الکتریسیته و مغناطیس شروع به
اوج گرفتن نمود. فارادی تحقیقاتی را که قبلاً بوسیله هانس کریستین اورستد[218] انجام گرفته بود دنبال کرد و کشف کرد اگر در سیمپیچی که در
نزدیکی یک آهنربا قرار دارد، الکتریسیته در جریان باشد، این باعث بوجود آمدن نیرو
میشود. همین پدیده است که بعدها اساس کار موتور الکتریکی قرار گرفت.
علائق
تحقیقاتی او تحتالشعاع مشاغل مدیریتی و آموزشی قرار گرفت، گرچه اینها تاثیر خیلی
خوبی نیز بر کارهای او گذاشتند. در 1826 او دست به یک سری از سخنرانیهای شبانگاهی
زد، و درسهای کریسمس برای جوانان را نیز شروع کرد. هر دو این برنامهها هنوز هم
برگزار میشوند. امروزه درسهای کریسمس از تلویزیون پخش میشوند. همین
تلویزیونی که ما اکنون از آن استفاده میکنیم، وسیلهای است که تنها به سبب کشفیات
فارادی اختراع شد. هنگامی که او در سال 1831 آزمایشهای خود را از سر گرفت، القاء
الکترومغناطیسی را کشف کرد. این کشفی بود که چهره صنعت در قرن نوزدهم را بکلی
تغییر داد، زیرا به اختراع موتورها و ژنراتورهای الکتریکی منجر شد. این آزمایشات
وی را متقاعد کرد که الکتریسیته، بر خلاف اینکه قبلاً تصور میشد، یک جریان سیال
نیست، بلکه باید نوعی از نیرو باشد که میان اجزاء ماده اعمال میشود.
موفقیت در
کارهای علمی معمولاً به کسب مناصب مدیریتی منجر میشود، که این خود باعث کاسته شدن
و اتلاف فعالیتهای علمی میشود. فارادی مشاور علمی ترینیتی هاوس بود، که
وظیفه آن حفظ امنیت آبراهها، برای تردد کشتیها در امپراطوری بریتانیا بود. او یک
نوع لامپ نفت-سوز اختراع کرد که خیلی کارآمد بود و میتوانست نور بیشتری تولید
کند. در 1840 او به سمت عضو کهنسال فرقه ساندمانیان منصوب شد، ولی وضعیت سلامتی او
رو به وخامت گذاشت. در 1858، به او یک منزل مجلل در هامپتون کورت، کاخ قبلی هانری
هشتم، داده شد. او در سال 1867 فوت کرد و در گورستان ”هایگیت“ بخاک سپرده شد.

اختراعات
فارادی باعث انقلابی در قرن نوزدهم شد، ولی (شاید بدلیل فقدان تحصیلات دانشگاهی)
او در نظریه پردازی ضعیف بود، و توضیح او درباره عملکرد اختراعاتش بیشتر بر پایه
تمثیلات مکانیکی قرار داشت. در 1831، یعنی همان سالی که فارادی کشف کرد چگونه
مغناطیس را به الکتریسیته تبدیل کند، یک وکیل اسکاتلندی صاحب پسری شد، که تنها
فرزندی بود که برایش باقی ماند. این وکیل بیشتر علاقه داشت تا به امور زمینداری
خود سرگرم باشد، ولی توجه زیادی نیز به وضعیت تحصیلی پسر جوانش ”جیمسی“ نشان میداد.
جیمسی بعدها به ”جیمز کلرک ماکسول[219]“ معروف شد.
جیمسی
باهوش و عاشق ماشینآلات بود. او کنجکاو بود و همیشه میپرسید ”این دستگاه چطور
کار میکند؟“ پدرش، که او نیز، علائق مشابهی داشت، سعی میکرد به بهترین شکل پاسخ
او را بدهد، و درصورتیکه پدرش از جواب دادن ناتوان بود، جیمسی سئوال مکمل دیگری را
میپرسید: ”این دستگاه به چه درد میخوره؟“
وقتی جیمز
نه ساله بود مادرش بر اثر ابتلاء به سرطان درگذشت؛ این فقدان، باعث نزدیکی بیشتر
پدر و پسر شد. پسر برای ادامه تحصیل به آکادکی ادینبورگ فرستاده شد. جیمز، آنگونه
که معلمانش از او انتظار داشتند نبود، ولی این نمیتوانست برای پدرش، که عاشق
تمیزی و آراستگی بود، مانعی باشد تا برایش لباسها و کفشهای مخصوص سفارش ندهد.
شاگردان دیگر به او لقب ”لوس“ داده بودند. ولی جیمز توانست با پافشاری خود احترام
آنها را جلب کند.
مدرسه یک
فایده مهم برای جیمز داشت و آن این بود که وی را به ریاضیات علاقهمند ساخت. یکبار
در نامهای که به پدرش نوشت، به ساختن چندظلعیهای گوناگون اشاره کرد. در سن
14 سالگی او برنده جایزهای شد که در آن مستقلاً نوعی منحنیهای ریاضی را اختراع
کرد، که بنام بیضیهای دکارتی شناخته میشوند. مقاله او در انجمن سلطنتی ادینبورگ
قرائت شد.
جیمز شعر
هم میسرود، ولی استعداد او در ریاضیات بیشتر بود. او در سن شانزده سالگی به
دانشگاه ادینبورگ رفت، و بعداً تحصیلات خود را در دانشگاه کمبریج، که مرکز اصلی ریاضیات
انگلسان بشمار میرفت، ادامه داد. ویلیام هاپکینز که معلم او برای امتحاناتش
بود میگوید که ”جیمز خارقالعادهترین مردی بود که تاکنون دیدهام“.
جیمز مدرک
کارشناسی خود را از دانشگاه کمبریج دریافت کرد، و برای ادامه تحصیلات در همانجا
ماند. درهمان موقع او شروع به آزمایشاتی درباره نور کرد. پس از آن کتاب فارادی
بنام تحقیقات تجربی را خواند و شروع به مطالعه درباره الکتریسیته نمود. اگر
بخواهیم خلاصه بگوییم، او در سال 1864مدل مکانیکی فارادی از پدیده الکترومغناطیس
را گرفت و آنرا بصورت دستگاهی از چهار قانون ریاضی خلاصه کرد (آن زمان، این قوانین
از چهار تا بیشتر بود، ولی امروزه ما با استفاده از نماد نویسی برداری، آنها را به
چهار گروه تقسیم میکنیم. برخی از فورمولبندیها نیز هستند که این قوانین را تنها
بصورت یک فرمول ارائه میدهند). این قوانین الکتریسیته و مغناطیس را بصورت دو
”میدان“ مختلف توصیف میکند که در سرتاسر فضا گسترده شده. یکی از این میادین
الکتریکی است و دیگری مغناطیسی. این میدانها نه فقط نشان دهنده شدت الکتریکی و
مغناطیسی هستند، بلکه جهت آنها را نیز در هر نقطه از این میدان مشخص میکنند.
چهار
فرمول مذکور معنای فیزیکی سادهای دارند. دو تای آنها به ما میگوید که الکتریسیه
و مغناطیس نه میتواند بوجود آید و نه میتواند نابود شود. سومی توضیح میدهد که
چگونه یک میدان مغناطیسی، که بر حسب زمان تغییر میکند، بر میدان الکتریکی اطرافش
تاثیر میگذارد. این همان کشف فارادی در مورد القاء الکترومغناطیسی است که بصورت
ریاضی بیان شده. فرمول چهارم توضیح میدهد که چگونه یک میدان الکتریکی، که بر حسب
زمان تغییر میکند، بر میدان مغناطیسی اطرافش تاثیر میگذارد. این فرمولها، حتی
اگر بصورت شفاهی هم بیان شوند، باز هم متقارن و زیبا هستند.
یک
دستکاری ساده در این چهار معادله، باعث تایید چیزی میشود که خود ماکسول از خیلی
وقت پیش به آن ظن داشت، و آنهم این بود که نور شکلی از امواج الکترومغناطیسی است،
بعبارت دیگر، نور نوعی اختلالِ درحال گسترش در میدانهای الکتریکی و مغناطیسی است.
خیلی ساده
میشد از معادلات ماکسول استدلال ریاضی مسئله را استنتاج کرد، چیزی که همه
ریاضیدانان آنرا بعنوان ”معادله موج“ میشناسند، و همانگونه که از نام آن پیداست
توصیف کننده این است که امواج چگونه منتشر میشوند. معادلات مکسول همچنین میتوانند
سرعت این چنین امواجی را نیز پیشبینی کنند، و اینکه آنها باید با سرعت نور حرکت
کنند.
تنها یک
چیز میتواند با سرعت نور حرکت کند، و آنهم چیزیست که خودش از جنس نور باشد.
در آن
زمان تصور بر این بود که یک محیط مادی باید وجود داشته باشد تا امواج در آن موج
بزنند. بعبارت دیگر باید رسانهای باشد که این امواج را منتقل کند؛ در حقیقت امواج
ارتعاشات رسانه هستند. بدیهیترین رسانه برای امواج نوری ایثر بود. ریاضیات حکم میکرد
که امواج نوری باید در جهتی به ارتعاش درآید که بر جهت حرکت آنها عمود است. همین
مورد بود که موجب سردرگمی نیوتون و هویگنس شده بود: آنها تصور میکردند که امواج
در امتداد حرکت موج مرتعش میشوند.
نظریه
ماکسول پیشبینی دیگر نیز میکرد و آن عبارت از این بود که ”طول موج“ امواج
الکترومغناطیسی، یا فاصله میان دو موج متوالی، میتواند هر عددی باشد. طولموج
نور بسیار کوتاه است، ولی باید امواج الکترومغناطیسی دیگری وجود داشته باشند که
طول آنها از نور بلندتر است. این نظریه آنقدر جذاب بود تا به هاینریش هرتز[220] انگیزه دهد تا این امواج را تولید کند. امروزه چنین امواجی،
”امواج رادیویی“ نامیده میشوند. گولیلمو مارکونی[221] سریعاً این مسئله را دنبال کرد و یک فرستند
و گیرنده برای آن ساخت، و بناگهان انسانها توانستند از یک سو تا سوی دیگر جهان،
بصورت آنی، با یکدیگر صحبت کند. برپایه همین اختراع ما تصاویر را مخابره میکنیم،
با رادار آسمانهای خود را زیر نظر داریم، و با دستگهاهای مکان یاب ماهوارهای (یا
GPS[222])
موقعیت خود را مشخص میکنیم.
متاسفانه
مفهوم ایثر مشکلساز بود. اگر ایثر وجود داشت پس زمین هم که بدور خورشید میگردد،
باید نسبت به ایثر در حرکت باشد. در اینصورت یا باید این حرکت را آشکار کرد، و یا
باید هر مفهومی را که با آزمایشهای انجام گرفته سازگاری نداشته باشد کنار گذاشت.
پاسخ این
مسئله بغرنج، بکلی چهره فیزیک را تغییر داد.

در
تابستان 1876 بنگاه تجاری ”ایزرائل و لِووی“ که توسط دو بازرگان یهودی در شهر اولم
آلمان مدیریت میشد یک شریک تازه گرفت: نام این شریک هرمان اینشتین بود. هرمان در
جوانی قابلیتهای قابل توجهای در ریاضیات از خود نشان داده بود، ولی والدینش بعلت
تنگدستی نتوانستند او را به دانشگاه بفرستند. حالا او در شرکتی شریک شده بود که
کارش فروش تُشکِ بود.
در اگوست
1878، هرمان در کنیسه اشتوتگارت با پائولین کوک ازدواج کرد، و نهایتاً آنها در
خانهای نزدیک ایستگاه قطار در بانهوفستراسه، سکنی گزیدند. کمتر از هشت ماه بعد،
اولین پسر آنها بدنیا آمد. در گواهی ولادتی که از اسناد ثبت شده باقی مانده اینطور
نوشته شده: ”یک طفل مذکر، با نام آلبرت، در شهر اولم در منزل مسکونی هرمان اینشتین
و همسرش، پائولین کوک،که به دین یهود متدین هستند متولد شد.“ پنج سال بعد خواهر
آلبرت، ماریا، هم بدنیا آمد، و این دو با یکدیگر خیلی انس گرفتند.
والدین
آلبرت نسبت به امور مذهبی رویکردی ملایم داشتند و سعی میکردند تا خود را با فرهنگ
محلی همساز کنند. در آن زمان، بسیاری از یهودیان آلمان، بدلیل اینکه میخواستند با
شهروندان دیگر مذاهب رابطه بهتری داشته باشند، با کاستن از آداب و ستنهای دینی،
خود را با جامعه ”تطبیق“ میدادند. نامهای که هرمان و پاوئولین برای فرزندان خود
انتخاب کردند، نامهای سنتی یهودی نبود، گرچه برای احترام به پدربزرگش آبراهام، نام
او را به نام آلبرت اضافه کردند. در خانه هرمان اینشتین، مذهب موضوعی نبود که هر
روزه بر سر آن صحبت شود، و آلبرت نیز در خانه پدری چیز زیاد از سنتهای یهودی یاد
نگرفت.
منبع
اطلاعات اصلی ما برای زندگی و شخصیت ابتدایی اینشتین، خاطرات کودکی ماریا است که
در سال 1924 به چاپ رسید. ظاهراً درهنگام تولد، بزرگی و گوشهدار بودن سرش موجب
وحشت مادرش شده بود. او هنگامی که نوزادش را برای اولین بار دیده بود فریاد زده
”سرش خیلی بزرگ است! خیلی بزرگ!“ هر چقدر که زبان بازکردن آلبرت بیشتر طول میکشید،
ترس از اینکه این پسر بعدها به یک معلول ذهنی بدل شود، بیشتر قوت میگرفت. ولی
آلبرت تا زمانی که از خود اطمینان پیدا کرد زبان نگشود و صبر کرد. او بعدها در
خاطراتش گفت که او فقط وقتی شروع به حرف زدن کرد که میتوانست کل جمله را ادا کند،
نه تکههایی از آن را. او در ذهن خود جملات را بررسی میکرد، و هنگامی که
مطمئن میشد کلمات در جای درست خود قرار دارند، آنها را به زبان میراند.
مادر
آلبرت پیانو نواز ماهری بود. مابین سنین شش و سیزده، شخصی بنام اشمید به آلبرت
ویولن درس میداد. هرچند در کودکی این درسها برایش ملال آور بود، ولی بعدها به
ویولن خود دلبسته شد.
کار فروش
تشک با شکست روبرو شد و هرمان با همکاری برادرش، جاکوب، به حرفه آبرسانی و گاز روی
آورد. جاکوب هم مهندس بود، و هم سرمایهگذار. دو برادر روی پروژههای جدید سرمایهگذاری
سنگینی کردند. پس از آن جاکوب تصمیم گرفت با ورود به صنعت برق، و ساخت تجهیزات
برای نیروگاهها، کار خود را تنوع بخشد. آنها در سال 1885 شرکت خود را تاسیس
کردند، و دو برادر با کمک مالی پدر پائولین و دیگر اعضای خانواده، به خانهای در
مونیخ نقل مکان کردند. در ابتدا کار آنها رونق داشت و ”شرکت صنایع الکتریکی جاکوب
اینشتین و شرکا“[223]، از حوزه شهر مونیخ گرفته تا شهرهایی در
ایتالیا، تجهیزات نیروگاهی میفروخت.
اینشتین
بعدها تعریف میکند که علاقه او به فیزیک هنگامی شکل گرفت که پدرش یک قطبنما را
به او نشان داد. هنگامی که چهار یا پنج سال داشت، آلبرت از اینکه میدید از هرطرف
که این قطبنما را میچرخاند همیشه یک جهت را نشان میدهد، شیفته آن شده بود. این
اولین بار بود که او طعم شگفتیهای رمزآلود فیزیک را میچشید. او این واقعه را
بسیار اسرارآمیز توصیف میکند.
آلبرت در
مدرسه شاگرد زرنگی بود، ولی از ابتدا استعداد خاصی را از خود بروز نداد. او کُند
بود و طوطیوار عمل میکرد، نمرههای خوبی کسب میکرد، ولی با دیگران کمتر خو میگرفت.
او ترجیح میداد به روش خودش بازی کند؛ او عاشق این بود که با روی هم گذاشتن ورقهای
بازی خانه درست کند. از ورزش متنفر بود. هنگامی که در سال 1888 به دبیرستان رفت،
برای یادگیری لاتین از خود استعداد نشان داد، و تا هنگامی که در پانزده سالگی آنجا
را ترک کرد، در لاتین و ریاضیات همیشه شاگرد اول بود. تواناییهای ریاضی او توسط
عمو جاکوب، که یک مهندس بود، و تا حدی ریاضیات پیشرفته میدانست، برانگیخته شد.
جاکوب برای آلبرت جوان مسائل ریاضی طرح میکرد، و آلبرت هنگامی که آنها را حل میکرد
بسیار خوشحال میشد. یکی از دوستان خانوادگی آنها بنام ماکس تالمود، تاثیر بسزایی
روی تحصیلات آلبرت گذاشت. تالمود دانشجوی فقیری بود که به تحصیل پزشکی مشغول بود،
و هرمان و پائولین هر پنجشنبه او را برای شام به خانه خود دعوت میکردند. او به
آلبرت تعدادی کتاب ساده درباره علوم داد؛ آنگاه او پسر جوان را با نوشتههای فلسفی
امانوئل کانت[224] آشنا ساخت. آنها ساعتها درباره موضوعات مختلف فلسفی و ریاضی به
بحث میپرداختند. تالمود بعدها نوشت که او هرگز ندیده بود که اینشتین با بچههای
دیگر بازی کند، و موضوعاتی را که مطالعه میکرد که از مباحث جدی بودند. تنها سرگرمی
او نواختن موسیقی بود، از جمله آثار بتهوون و موتسارت که در آن مادرش، پائولین، او
را با پیانو همراهی میکرد.
اشتیاق
آلبرت برای ریاضیات وقتی تقویت شد که در سال 1891 نسخهای از کتاب اصول اقلیدس
بدستش رسید، کتابی که بعدها از آن بنام ”کتاب مقدس هندسه“ یاد میکرد. آنچه که
بیش از هر چیز او را تحت تاثیر قرار داده بود وضوح استدلالات، و روشی بود که
اقلیدس ایدههای مختلف را در کنار هم جمع کرده بود. بدلیل تعلیمات دینی اجباری در
مدرسه، آلبرت برای مدتی مذهبی شده بود. ولی هنگامی که او با علم مواجه شد، همه
اینها رنگ باختند. مطالعات او درباره تورات و اشتیاقش نسبت به جشن تکلیف دینی[225] ناگهان کاسته شد؛ ندای دیگری آلبرت را فرامیخواند.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
”تقریباً
همه چیزها قبلاً کشف شدهاند، و آنچه باقیمانده تنها روزنههایی است که باید پر
شود.“ این سخنان خبر مایوس کنندهای برای جوانان با استعدادی است که میخواهند در
رشته فیزیک تحصیل کنند، خصوصاً وقتی از زبان فیزیکدان مشهوری همچون فیلیپ فون جولی[257] مطرح شود.
سال 1874
بود و دیدگاه جولی منعکس کننده نظر بیشتر فیزیکدانان آن زمان بشمار میرفت: از نظر
آنها کار فیزیک پایان یافته بود. در سال 1900، لورد کلوین که چهره برجستهای محسوب
میشد گفت ”حالا دیگر چیز جدیدی برای کشف شدن در فیزیک نیست. آنچه باقی مانده تنها
انجام آزمایشهای دقیق، و بازهم دقیقتر است.“
محض اطلاع
شما، او جملات دیگری را اظهار کرده: ”میتوانم به جرأت بگویم که حرکت ماشینهای
سنگینی که در هوا حرکت کنند غیر ممکن است ... فرود بر سطح ماه چنان مسائل دشواری
را پیش روی انسان قرار میدهد که مرتفع کردن آنها 200 سال دیگر به طول میانجامد“.
زندگینامه نویس کلوین در جایی نوشت ”او نیمه اول عمرش را در حالی سپری کرد که حق
با او بود، و نیمه دوم عمرش را در اشتباه گذراند“.
ولی
چیزهایی که او میگفت تماماً غلط نبود. در یکی از جلسات درسش، با عنوان ”ابهامات
نظریه دینامیک گرما و نور در قرن نوردهم“ که در سال 1900 برگزار شد، او انگشت خود
را بر روی دو اختلاف عمده گذاشت که از شناخت جهان فیزیکی وجود داشت: ”در حال حاضر
زیبایی و صراحت نظریه دینامیک، که میگوید گرما و نور حالاتی از حرکت هستند، دارای
دو ابهام است. اولی در بردارنده این پرسش است که چگونه زمین میتواند در درون یک
محیط کشسان حرکت کند، آیا این همان ایثر تابناک است؟ و دومی به اصل ماکسول-بولتزمن
درباره افراز انرژی ربط دارد.“ اولین ابهام به نظریه نسبیت، و دومی به نظریه
کوانتوم منتهی شد.
خوشبختانه
یکی از شنوندگان جولی از نصایح او هراسی به خود راه نداد. او زمانی گفت که وی
اشتیاقی برای کشف چیزهای جدید ندارد، بلکه آنچه میخواهد تنها این است که درک
بهتری از اصول فیزیک داشته باشد. در جستجو برای این درک بهتر، او یکی از ابهاماتی
که کلوین از آنها صحبت کرده بود را پس زد، و بانی یکی از دو نظریه انقلابی فیزیک
قرن بیستم گشت. نام او ماکس پلانک[258] بود، و نظریهاش فیزیک کوانتوم نام گرفت.

جولیوس
ویلهلم پلانک، یک استاد حقوق در مونیخ بود. پدر و مادرش هر دو استاد الهیات بودند،
و برادرش هم قاضی بود. بنابراین وقتی همسر دومش، اِما پتزیگ، برای جولیوس یک پسر
بدنیا آورد (فرزند ششم او)، معلوم بود که این پسر در یک محیط روشنفکر رشد میکند.
ماکس کارل ارنست لودویگ پلانک در 23 آوریل 1858 بدنیا آمد. در آن زمان اروپا در
آشفتگی سیاسی بسر می برد، و خاطرات کودکی او شامل دیدن نیروهای پروس و اطریش بود
که در سال 1864 در شهر کیل رژه میرفتند.
در سال
1867 خانواده پلانک به مونیخ نقل مکان کرد، و ماکس توسط ریاضیدانی بنام هرمان مولر
در مدرسه شاه ماکسیملیان آموزش دید. مولر به پسر جوان ریاضی، نجوم، مکانیک، و اصول
فیزیک درس میداد، که شامل قانون بقاء انرژی هم بود. پلانک دانشآموز بسیار
بااستعدادی بود، و زودتر از موعد، در سن 16 سالگی فارغالتحصیل شد.
او در
موسیقی نیز استعداد داشت، ولی علیرغم اندرزهای جولی، او تصمیم گرفت تا در رشته
فیزیک تحصیل کند. پلانک زیر نظر جولی چندین آزمایش انجام داد ولی خیلی زود بسمت
فیزیک نظری متوجه شد. او در برلین تحت نظر دانشمندان برجستهای همچون هلمهولتز،
گوستاو کیرشهف، و وایرستراس تحصیل کرد. او اولین آزمون خود را در سال 1878 گذراند
و در سال 1879 دکترای خودش را در زمینه ترمودینامیک کسب کرد. برای مدتی در همان
دبیرستانی که قبلاً تحصیل میکرد ریاضی و فیزیک درس میداد. در سال 1880، رساله
فوق دکترای او در باره ”تعادل گرمایی اجسام در درجه حرارتهای مختلف“ پذیرفته شد، و
برای کسب یک شغل دائم دانشگاهی صاحب صلاحیت شد. البته چنین فرصتی هنگامی محقق شد
که دانشگاه کیل او را به سمت استادیار بکار گمارد. تحقیقات او بر روی ترمودینامیک،
و مخصوصاً مفهوم آنتروپی[259]، تمرکز داشت.
ماکس با
خواهر یکی از دوستانش بنام ماری مِرک آشنا شد، و در سال 1887 با یکدیگر ازدواج
کردند. آنها کلاً صاحب چهار فرزند شدند: اما و گرته، که دو قلو بودند، کارل و
اروین.
در 1889،
همان سالی که دو قلوها متولد شدند، ماکس جانشین کیرشهف در برلین شد و در سال 1892
به مقام استادی رسید. خانواده او به ویلایی در گرونوالد در حومه برلین نقل مکان
کرد، جایی که برخی از استادان دیگر نیز در همان نزدیکیها زندگی میکردند. یکی از
آنها استاد الهیاتی بود که آدولف فون هارناک نام داشت، که بعداً دوست صمیمی پلانک
شد. پلانک و همسرش اهل معاشرت بودند، و روشنفکران مشهور مرتباً به خانه آنها رفت و
آمد داشتند. اشخاصی از قبیل اینشتین، اتو هان[260] و لیزه مایتنر[261]، که بعداً کشفیات مهمی در باره شکاف هستهای
انجام داد که نهایت به ساخت بمب اتمی انجامید، از جمله کسانی بودند که با خانواده
پلانک رفت و آمد داشتند. از زمان هلمهولتز سنتی بجامانده بود که در گردههمآییهای
نظیر این موسیقی نواخته شود، و پلانک نیز در مهمانیهای خود این سنت را ادامه داد.
برای مدتی
آنها روزگار خوب و درخشانی داشتند، تا آنکه همسرش ماری به یک بیماری ریوی
(احتمالاً سل) مبتلا شد و در سال 1909 درگذشت. یک سال و نیم بعد، ماکس برای بار دوم
در سن 52 سالگی با مارگا فون هوسلین ازدواج کرد، که از او نیز صاحب پسری بنام
هرمان شد.

در سال
1894 یک شرکت محلی که در کارهای الکتریکی دست داشت به ساختن لامپهای برقی روی آورد
که کارآمدتر بود، به همین دلیل ماکس هم با این شرکت یک قرارداد تحقیقاتی منعقد
کرد. از نظر تئوری، تجزیه و تحلیل لامپهای الکتریکی، و اینکه چگونه نور بوسیله یک
جسم کاملاً غیرقابل انعکاس تابش میکند، در یک مسئله استاندارد فیزیک جای داشت که
به آن ”تابش جسمسیاه[262]“ میگفتند. هنگامی که چنین جسمی گرم شود،
نوری با تمام فرکانسها از خود تابش میکند، ولی شدت نور (که با انرژی آن همارز
است) با کم و زیاد شدن فرکانس تغییر میکند. سئوال اساسی این بود که چگونه فرکانس
بر روی شدت نور تاثیر میگذارد؟ با بیتوجهای به چنین مسئله مهمی، بعید بنظر میرسید
که بتوان لامپهای بهتری اختراع کرد.
نتایج
تجربی خوبی در دسترس بود، و از روی اصول فیزیک کلاسیک، یک قانون نظری بنام قانون
رایلی-جینز، هم استنتاج شده بود. متاسفانه این قانون هنگامی که فرکانسها خیلی
بالا میرفت با شواهد تجربی مطابقت نداشت. در حقیقت، این قانون چیزی را پیشبینی
میکرد که غیر ممکن بود: همانطور که فرکانس نور افزایش پیدا میکند، انرژی آن باید
بصورت بینهایتی بزرگ شود. این نتیجه ناممکن، به ”فاجعه فرابنفش[263]“ معروف شد. آزمایشات بعدی به قانون جدیدی
منجر شد، که به افتخار کاشف آن، ویلهلم وین[264]، قانون وین نامیده شد.
ولی قانون
وین هنگامی که فرکانس تابشها خیلی کم میشد اشتباه جواب میداد.
فیزیکدانان
با دو قانون مواجه بودند: یکی از آنها برای فرکانسهای بالا جواب میداد و دیگری
برای فرکانسهای پائین. این ایده به ذهن پلانک خطور کرد که چطور میشود از میان این
دو، یک درونیابی ریاضی انجام داد، به این صورت که آن عبارات ریاضی که قانون
رایلی-جینز (برای فرکانسهای بالا)، و همچنین قانون وین (برای فرکانسهای پائین)، را
بیان میکند در یکجا نوشت، و از میان آنها یک تقریب بدست آورد. فرمول حاصله، حالا
به ”قانون پلانک برای تابش جسمسیاه“ معروف است.
این قانون
جدید عمداً طوری طرح ریزی شده بود که بخوبی با نتایج آزمایشاتی که در گستره تمام
فرکانسهای تابش الکترومغناطیسی انجام میشود تطابق داشته باشد. ولی این قانون
صرفاً جنبه تجربی داشت (از آزمایشات ناشی شده بود، و نه از هیچ یک از اصول
فیزیکی). پلانک، که با خودش عهد بسته بود تا فیزیک را بهتر درک کند، زیاد از این
مسئله راضی نبود و در تلاش بود تا اصول فیزیکی را پیدا کند که میتوانست این قانون
را توجیه کند.
سرانجام
پلانک در سال 1900 متوجه ویژگی خاصی در فرمول خود شد. اگر او در فرمول خود تغییر
کوچکی میداد، بوسیله همان محاسباتی که رایلی و جینز انجام داده بودند، او نیز از
همان طریق میتوانست فرمول خود را بدست آورد. رویکرد کلاسیک بر این فرض استوار بود
که انرژی الکترومغناطیسی هر فرکانس، هر مقداری را میتواند داشته باشد. بویژه
میتواند تا هرقدر که بخواهیم به صفر نزدیک باشد. پلانک متوجه شد که همین فرض است
که باعث ”فاجعه فرابنفشی“ میشود، و اگر او فرض دیگری را در نظر بگیرد، آن
”بینهایت مشکلساز“ از مسئله حذف میشود.
ولی آن
فرضی که باید در نظر گرفته میشد چیز سادهای نبود و یک فرض بنیادی بود. انرژی
تابشی یک فرکانس مفروض، باید بصورت عددهای صحیحی از بستههای انرژی با اندازه ثابت
باشد. در حقیقت اندازه هر یک از این بستهها باید با فرکانس مربوطه متناسب باشد
(یعنی مساوی باشد با حاصلضرب فرکانس در یک عدد ثابت، که حالا ثابت پلانک نامیده
میشود و آن را به h
نمایش میدهیم.)
این بستههای
انرژی کوانتا نامیده میشدند (کوانتا مفرد لغت کوانتوم در زبان لاتین است). پلانک
نور را بصورت کوانتومی (بصورت بستهای) تعریف کرد.
خیلی خوب،
پس چرا هیچ وقت آزمایشگران متوجه این مسئله نشدند که انرژی همیشه بصورت بستههایی
وجود دارد که تعداد آنها اعداد صحیح هستند؟ پلانک با مقایسه محاسبات خودش و انرژیهای
که در آزمایشات مشاهده میشود، توانست اندازه آن ثابت را بدست آورد، و معلوم شد که
مقدار آن بسیار، بسیار، بسیار کوچک است. در حقیقت مقدار h برابر است با 34-
10 × 6 ژول در ثانیه. قطع نظر از جزئیات، برای مشاهده ”اختلافها“ در محدوده
انرژیهای ممکن (یعنی مقادیری که فیزیک کلاسیک اجازه آنرا میدهد، ولی فیزیک
کوانتوم نه) آزمایشات شما باید تا رقم 34ام اعشار دقیق باشد. حتی امروزه هم بسختی
میتوان یک کمیت فیزیکی را با دقتی بیش از شش یا هفت رقم اعشار اندازه گرفت، و در
اواخر قرن نوزدهم دقت اندازهگیریها بسیار کمتر از این بود. مشاهده مستقیم کوانتا
به چنان سطحی از دقت نیاز دارد که محال است.
عجیب بنظر
میرسد که اختلافی در این حد کوچک بتواند تاثیری چنین ژرف بر قانون تابش
الکترومغناطیسی بگذارد. ولی محاسبه قانون تابش مستلزم افزودن سهم کلیه فرکانسهای
ممکن بر روی انرژی است. حاصل چیزی است که از تاثیر جمعی کلیه کوانتاهای ممکن بدست
میآید. شما نمیتوانید بر روی کره ماه بایستید و دانههای شنی که بر روی زمین
قرار دارد را از یکدیگر تشخیص دهید. ولی بخوبی میتوانید صحرای آفریقا را ببینید.
اگر واحدهای کوچکتر به اندازه کافی با هم ترکیب شوند، نتیجه آن میتواند عظیم
باشد.
زندگی
حرفهای پلانک پیشرفت کرد، ولی زندگی شخصی او پر از مصیبت بود. پسرش کارل در
عملیاتی در جنگ جهانی اول کشته شد. دخترش گرته هنگام وضع حمل در 1917 مرد، دختر
دیگرش اما نیز که با بیوه خواهرش ازدواج کرده بود، در سال 1919 از همین عارضه جان
داد. چند سال بعد، پسرش اروین نیز بدلیل شرکت در سوء قصد نافرجامی که در سال 1944
بر علیه آدولف هیتلر انجام گرفت، اعدام شد.

در سال
1905 شواهد تازهای، که بر اساس کارهای اینشتین بر روی اثر فتوالکتریک قرار داشت،
آشکار شد و از نظریات انقلابی پلانک پشتیبانی کرد. بخاطر دارید که اثر فتوالکتریک
در مورد کشفی بود که اینشتین درباره تبدیل نور به الکتریسیته انجام داده بود.
اینشتین میدانست که الکتریسیته بصورت بستههای مجزا از هم است. درواقع، در آن
زمان دانشمندان میدانستند که الکتریسیته حرکت ذرات ریزی بنام الکترون است.
اینشتین بر اساس پدیده فتوالکتریک نتیجه گرفت که این پدیده در مورد نور هم باید
صادق باشد. این مورد نه فقط نظر پلانک در مورد کوانتایی (بستهای) بودن نور را
تائید میکرد، بلکه نشان میداد این بستهها چه هستند: امواج نور هم، مانند الکترونها،
باید نوعی ذره باشند.
چگونه یک
موج میتواند ذره باشد؟ در هر حال، این چیزی بود که آزمایشات نشان میداد و باید
چگونگی آن مشخص میشد. کشف ذرات نور، یا فوتونها، سریعاً به تصویری کوانتومی از
جهان انجامید که در آن ذرات بواقع موج بودند، و برخی اوقات مانند موج رفتار میکردند
و برخی مواقع مانند ذره.
فیزیکدانان
شروع کردند تا کوانتا را جدیتر بگیرد. فیزیکدان بزرگ دانمارکی نیلز بور[265] یک نوع مدل کوانتومی از اتم ارائه داد، که در آن الکترونها در مدارهای
دایرهای به دور هسته مرکزی گردش میکردند، و اندازه مدار به اجزاء کوانتا محدود
میشد. فیزیکدان فرانسوی لویی دو بروی[266] استدلال کرد که بدلیل اینکه فوتونها میتوانند
هم موج باشند و هم ذره، و هنگامی که برخی از فلزات با فوتون برخورد کنند از آنها
الکترون ساطع میشود، بنابراین الکترونها نیز باید ماهیت دوگانهای داشته
باشند، و هم ذره باشند و هم موج. درحقیقت، ماده باید چنین ماهیت دوگانهای داشته
باشد (یعنی برخی اوقات ذره صُلب باشد، و برخی اوقات هم مانند امواجِ درحال نوسان).
به همین دلیل هم هست که آزمایشات میتوانند بر هر دو شکل آنها دلالت کنند.
نه ”ذرهای
بودن“، و نه ”موجی بودن“ هیچکدام نمیتواند رفتار ماده را در مقیاسات بسیار کوچک
توضیح دهد. اجزاء تشکیل دهنده ماده، پارههایی از هر دو هستند که موجذره[267] نامیده میشود. دو بروی فورمولی برای تشریح
موجذرهها اختراع کرد.
پس از آن
یک گام کلیدی برداشته شد، که به داستان ما ربط زیادی دارد. اروین شرودینگر[268] فرمول دوبری را گرفت و آنرا بدل به معادلهای کرد که میتوانست
حرکت موجذرات را توضیح دهد. همانگونه که معادلات حرکت نیوتون اساس مکانیک کلاسیک
را تشکیل میدهند، معادله شرودینگر نیز به اساس مکانیک کوانتوم بدل شد.
اروین که
در سال 1887 در وین بدنیا آمد، حاصل یک ازدواج میان فرقهای بود. پدرش رودولف
شرودینگر، یک کَفَندوز بود که در کار تولید پارچههای مومی مخصوص مردگان بود؛ او
یک گیاهشناس نیز بود. رودولف کاتولیک بود، درحالیکه مادر اروین، جورجین امیلیا
برندا، پروتستان بود. اروین مابین سالهای 1906 تا 1910 در وین، تحت نظر فرانز
اکسنر[269] و فریدریش هازناُهلر[270] به تحصیل فیزیک مشغول بود، و در سال 1911 دستیار
اکسنر شد. او دکترای تخصصی خود را در 1914، در همان هنگام که جنگ جهانی اول شروع
شد، اخذ کرد و در طول جنگ بعنوان افسر توپخانه در ارتش اتریش خدمت میکرد. دو سال
پس از پایان جنگ، او با آنهماری برتل ازدواج کرد. در 1920 او بسمت استادیار
دانشگاه اشتوتگارت منصوب شد، و در سال 1921 به سمت استادی ارتقاء پیدا کرد.
او طی
مقالهای که در سال 1926 منتشر کرد معادله معروف خود را ارائه کرد و در آن نشان
داد که این معادله سطوح انرژی صحیحی را برای اتم هیدوژن بدست میدهد. به
دنبال آن سه رساله مهم درباره نظریه کوانتوم منتشر کرد. او در سال 1927 به ماکس
پلانک که در برلین بود پیوست، ولی در 1933، بدلیل بیزاری از رفتار ضد-یهودی نازیها،
آلمان را به مقصد انگلستان ترک کرد و در آنجا به دانشگاه ماگدالن رفت. چیزی از
رسیدنش به انگلستان نگذشته بود که وی، به همراه پُل دیراک[271]، برنده جایزه نوبل در فیزیک شدند.
شرودینگر
سبک زندگی نامتعارف و رسوائیآمیزی داشت. او در یک خانه با دو زن زندگی میکرد، و
این برای دیگر استادان آزار دهنده بود. او بار دیگر نقل مکان کرد، این بار به
پرینستون آمریکا. در آنجا یک پست دائمی به او پیشنهاد شد، ولی وی آن را رد کرد
(شاید بدلیل وابستگی به همسر و معشوقهاش که هر دو در یک خانه با او زندگی میکردند).
زندگی در پرینستون هم بهتر از آکسفرد نبود. او در سال 1936 در شهر گراز اتریش سکنی
گزید، و بیتوجه به عقاید سختگیرانه اتریشیها، به شیوه زندگی خود ادامه داد.
اشغال
اتریش توسط هیتلر دشواریهای فراوانی را برای شرودینگر که یک ضد-نازی معروف بود
ببار آورد. او مجبور شد اعقاید قبلی خود را رد کند (و بعدها بخاطر اینکار از
اینشتین عذرخواهی کرد). این اقدامات فایدهای بهمراه نداشت: بدلیل اینکه او را از
نظر سیاسی غیرقابل اعتماد میدانستند کارش را از دست داد، و مجبور شد به ایتالیا
بگریزد.
عاقبت
شرودینگر در دابلین سکنی گزید. او در 1944 کتاب زندگی چیست؟ را منتشر کرد،
کتابی فریبنده ولی ناقص که سعی داشت فیزیک کوانتوم را در مسائل زیستشناسی بکار
گیرد. او نظرات خود را بر پایه مفهوم ”نگنروپی[272]“ گذاشته بود. نگنتروپی (آنتروپی منفی)،
تمایل حیات به نقض (یا شاید هم فروپاشی) قانون دوم ترمودینامیک است. شرودینگر
تاکید کرد که ژنهای موجودات زنده باید نوعِ خاص و پیچیدهای از ملکولها باشد، که
حاوی دستورالعملهای رمزی است. امروزه ما به این ملکولها DNA میگوئیم، ولی ساختار آنها تا
سال 1953 ناشناخته بود، تا آنکه، با الهام از نظرات شرودینگر، بوسیله فرانسیس کریک[273] و جیمز واتسون[274] کشف شد.
شرودینگر
در ایرلند زندگی بیبند و بار جنسی خود را ادامه داد، ودرگیر روابط با دانشجویان
خود شد و از دو زن مختلف صاحب دو بچه شد. او در سال 1961 بعلت ابتلاء به سل
درگذشت.

شرودینگر
بیشتر بدلیل گربهاش معروف است. البته گربه او واقعی نبود، و تنها در یک آزمایش
فکری نقش بازی میکرد. گربه شرودینگر بعنوان توضیح پشت پرده برای مسائلی تلقی میشوند
که پیآمدهای درستی دارند، ولی هرگز نمیتوان آنها را به لحاظ تجربی مورد سنجش
قرار داد. بااینحال چنین برداشتی بحثبرانگیز است (اگر موجها وجود ندارند، پس چرا
پیآمدهای آنها به این خوبی عمل میکنند؟)
باری، به
مسئله گربه بازگردیم. برطبق مکانیک کوانتوم، موجذرات میتوانند با یکدیگر تداخل
کنند، بر روی هم انباشته شوند و هنگامی که هر دو در اوج هستند همدیگر را تقویت، و
هنگامی که یکی در اوج و دیگری در افتادگی است همدیگر را خنثی کنند. این نوع رفتار
انطباق (یا برهمنهش)[275] نامیده میشود، بنابراین موجذرات کوانتومی
میتوانند درحالت برهمنهشی باشند (یعنی آنها میتوانند حالتهای گوناگونی داشته
باشند بدون اینکه بطور کامل در یکی از آن حالتها باشند.) در واقع برطبق ”برداشت
کپنهاگی“ از نظریه کوانتوم، این حالت عادی جهان است. تنها وقتی ما یک کمیت فیزیکی
را مشاهده میکنیم، آنرا وادار میکنیم که از حالت برهمنهشی خارج شود و یک حالت
منفردِ ”خاص“ به خود بگیرد.
این
برداشت بخوبی در مورد الکترونها جواب میداد، ولی شرودینگر میخواست بداند که آیا
این قضیه در مورد یک گربه هم صادق است یا نه. در آزمایش فکری او، گربهای هست که
در یک جعبه دربسته، و در حالتی از برهمنهش زنده و مرده قرار دارد. هنگامی که جعبه
را باز میکنید، شما یک مشاهد انجام میدهید و گربه را وادار میکنید که در یکی از
این حالات قرار بگیرد، یعنی گربه یا زنده است یا مرده. همانطور که پراچت در کتاب
تخیلی خودش بنام Maskerade
آورده، گربهها شبیه این نیستند. در آنجا گربه بزرگی بنام گریبو هست که وقتی در
جعبه باز شود حالت سومی را به خود گرفته: او کاملاً عصبانی و خونخوار میشود!
بدلایل
متفاوت دیگری، شرودینگر هم میدانست که گربهها اینطور نیستند. الکترون یک چیز
بسیار کوچک است، و در سطح کوانتومی رفتار میکند. این ذره (هنگامی که ما آن را
اندازهگیری میکنیم) دارای مکان، سرعت، یا اسپینی است که میتوان آن را خیلی ساده
بیان کرد. درمقایسه، گربه یک چیز نسبتاً درشت است و هیچ یک از خواص بالا را ندارد.
شما میتوانید الکترونها را بر همبنهید، ولی چنین کاری را در مورد گربهها نمیتوانید
انجام دهید. برای این مسئله اصطلاحی هست که ”ناهمدوسی[276]“ نام دارد و توضیح میدهد که چرا سیستمهای
بزرگی مانند گربه همانطوری بنظر میرسند که ما آنها را در زندگی روزانه خود میبینیم،
یعنی بصورتی که با باورهای کلاسیک مطابقت دارد. ناهمدوسی به ما میگوید که یک
گربه از آنچنان تعداد بیشماری از موجذرات تشکیل شده که همه با یکدیگر درهمتنیده
میشوند و برهمنهشتی را در آنچنان زمان کوتاهی خراب میکنند که مقدار آن از مدت
زمان لازم برای اینکه نور قطر یک الکترون را هم طی کند کمتر است. بنابراین، گربهها
که سیستمهای ماکروسکوپیک (قابل روئیت) هستند و از تعداد بیشماری ذرات کوانتومی
تشکیل شدهاند، مانند همان گربههایی که ما میشناسیم رفتار میکنند. آنها
یا میتوانند زنده باشند و یا مرده، ولی نه در آنواحد هر دو حالت.
اگرچه در
مقیاسی بیاندازه کوچک، (منظور از کوچک، آن چیزهایی هستند که حقیقتاً کوچکاند، و
نه آن چه شما میتوانید با یک میکروسکپ معمولی مشاهده کنید)، جهان همانگونه رفتار
میکند که مکانیک کوانتوم میگوید، و میتواند همزمان دو حالت مختلف داشته باشد.
این همان چیزی بود که بینش ما را بکلی تغییر داد.

اینکه
دنیای کوانتوم چقدر میتواند عجیب باشد، از تحقیقات ورنر هایزنبرگ[277] سرچشمه گرفته. هایزنبرگ یک فیزیکدان نظری برجسته بود، ولی دانش او
از فیزیک تجربی آنقدر کم بود که هنگام آزمون دکترای فیزیک حتی نمیتوانست به
سئوالات سادهای درباره تلسکوپ یا میکروسکوپ پاسخ دهد. او حتی نمیدانست که یک
باتری چگونه کار میکند.
آگوست
هایزنبرگ در سال 1899 با آنا وکلین ازدواج کرد. او پیرو کلیسای لوتری بود، و آنا
که یک کاتولیک بود مجبور شد آئین خود را تغییر دهد تا ازدواج آنها از لحاظ مذهبی
ممکن شود. آنها اشتراکات فراوانی داشتند: اگوست معلمی بود که تخصصش در ادبیات
کلاسیک و یونان باستان بود، درحالیکه آنا فرزند یک مدیر مدرسه بود، که او نیز
متخصص ادبیات یونانی بود. اولین فرزند آنها بنام ادوین در سال 1900 بدنیا آمد و
بعدها یک شیمیدان شد. فرزند دوم آنها، ورنر، در سال 1901 بدنیا آمد و منشا تغییرات
عظیمی در جهان شد.
در آن
زمان آلمان هنوز یک کشور سلطنتی بود، و شغل آموزگاری ارج و قرب فراوانی داشت. از
همین روی خانواده هایزنبرگ نیز آنقدر در رفاه بودند تا بتوانند پسران خود را به
مدارس تراز اول بفرستند. در سال 1910، پدر خانواده، آگوست، به سِمت استاد ادبیات
مدرن و قرون وسطایی یونان در دانشگاه مونیخ منصوب شد، و خانواده آنها به آنجا نقل
مکان کرد. در سال 1911 ورنر به مدرسه پادشاه ماکسمیلیان در مونیخ رفت، همانجایی که
پلانک هم دوران دبیرستان خود را در آن طی کرده بود. مدیر آن مدرسه پدر بزرگ ورنر،
نیکلاس وکلین، بود. بدلیل اینکه پدر ورنر همیشه پسرانش را تشویق میکرد که با یکدیگر
رقابت کنند، او باهوش و سریع بار آمده بود، و استعدادهای خود را در علوم و ریاضیات
بخوبی نشان داد. او در موسیقی نیز استعداد داشت، و آنچنان پیانو نوازی را خوب یاد
گرفته بود که در سن 12 سالگی در کنسرتهای مدرسه برنامه اجراء میکرد.
هایزنبرگ
بعدها نوشت: ”علاقه من به زبان و ریاضیات از همان ابتدای کودکی بیدار شد.“ او در
یونانی و لاتین نمرههای خوبی میگرفت، و همینطور ریاضیات، فیزیک و تعلیمات دینی
او نیز بسیار خوب بود. چیزی که در آن خیلی بد بود یکی ورزش بود و دیگری زبان
آلمانی. معلم ریاضی او، کریستوف ولف، معلم بسیار خوبی بود، و با مطرح کردن مسئلههای
خاص باعث شد تا تواناییهای ریاضی او گسترش یابد. بزودی شاگرد از استادش پیشی
گرفت، و مدرسه در گزارشی که برای پدر و مادرش فرستاد نوشت ”با کارهایی که او بطور
مستقل در حوزه ریاضی/فیزیک انجام داده، از سطحی که مدرسه میتواند برای او فراهم
آورد خیلی جلوتر رفته.“ او پیش خودش نسبیت را آموخت، درحالیکه محتوای ریاضی آن را
به معنای فیزیک آن ترجیح میداد. هنگامی که پدر و مادرش از وی خواستند تا به دختر
همسایهشان که دانشجو بود کمک کند، او نزد خودش حساب دیفرانسیل و انتگرال را
یادگرفت، موضوعی که جزء درسهای دبیرستان نبود. او علاقه خاصی به نظریه اعداد نشان
داد و میگفت ”همه چیز در این مبحث آنقدر واضح است که شما میتوانید آنرا تا آخر
درک کنید.“
پدرش برای
اینکه به ورنر کمک کند تا لاتین خود را بهتر کند، برایش تعدادی کتاب قدیمی ریاضی
خریده بود که به آن زبان نوشته شده بودند. از جمله آنها، رساله کرونکر درباره
تئوری جبری اعداد، بود. کرونکر، که یک متخصص تراز اول نظریه اعداد بود، اعتقاد
داشت ”خداوند اعداد صحیح را آفریده، و باقی کار آدمی است.“ هایزنبرگ چنان اشتیاقی
نسبت به نظریه اعداد از خود نشان داد که تا مدتی وقت خود را صرف اثبات آخرین قضیه
فرما کرد. پس از نه سال تحصیل مقدماتی، او درحالیکه شاگرد اول کلاس خود بود از
مدرسه فارغالتحصیل شد و پس از آن در دانشگاه مونیخ ثبت نام کرد.
هنگامی
که جنگ جهانی اول آغاز شد، متفقین آلمان را محاصره کردند. کشور از لحاظ غذا و سوخت
در مضیقه بود؛ مدارس بدلیل اینکه نمیتوانستند موجبات گرم کردن کلاسها را فراهم
آورند میباید تعطیل میشدند، و ورنر یکبار چنان از گرسنگی بیحال شد که از روی
دوچرخهاش به داخل گودالی افتاد. پدرش، بهمراه معلمان او، در ارتش خدمت میکردند؛
آنهایی که باقی میماندند تحت تعلیمات نظامی و میهنپرستانه قرار میگرفتند. پایان
جنگ با انقراض رژیم سلطنتی آلمان نیز همراه بود، و برای مدت کوتاهی ایالت باواریا
یک دولت سوسیالیست شبیه آنچه در شوروی بود داشت، ولی در 1919 سربازان آلمانی که از
برلین آمده بودند سوسیالیستها را بیرون، و یک نوع حکومت سوسیال دمکرات معتدلتر را
جایگزین آن کردند.
هایزنبرگ
نیز مانند اکثر هم عصران خود، با شکست آلمان از خواب غفلت بیدار شدند و پیشینیان
خود را باعث این شکست نظامی میدانستند. او رهبر یک دسته از جوانان بنام
”پیشاهنگان نوین“ شد، که هدف آنها بازگرداندن رژیم سلطنتی بود. آنها در آرزوی رایش
سوم بودند. خیلی از شاخههای پیشاهنگان نوین اعتقادات ضد-یهودی داشتند. ولی گروه
ورنر شامل تعدادی از پسران یهودی هم میشد. او مدت زمان زیادی را با افراد دسته
خود به پیادهروی و چادر زنی میگذراند و عموماً سعی داشت خاطرات دوران رمانتیک
آلمان را زنده کند، ولی اینها با روی کار آمدن هیتلر در سال 1933، و ممنوع شدن
کلیه فعالیتهایی که خارج از حزب نازی بود، پایان یافت.
ورنر در
بدو ورود خود به دانشگاه مونیخ در سال1920 میخواست در رشته ریاضیات محض تحصیل
کند، تا اینکه در صحبتی که با یکی از اساتید خود داشت از این کار صرف نظر کرد.
بجای آن، او تصمیم گرفت که تحت نظر آرنولد زومرفِلد[278] به مطالعه فیزیک بپردازد. زومرفلد که به
استعداد ورنر پی برده بود، به وی اجازه داد تا در کلاسهای پیشرفته او شرکت کند.
ورنر بزودی تحقیقات اصلی خود را بر روی ساختار کوانتومی اتم شروع کرد. او در 1923
بعنوان جوانترین کسی که دکترا میگیرد رکورد دانشگاه خود را شکست و فارقالتحصیل
شد. در همان سال، هیتلر سعی کرد که دولت ایالت باواریا را سرنگون کند ولی در اینکار
ناکام ماند. تورم شدید در همه جا شایع بود؛ آلمان داشت تکه تکه می شد.
ورنر به
کارش ادامه داد. او با بسیاری از فیزیکدانان برجسته که در زمینه فیزیک کوانتوم
کار میکردند همکاری داشت. او بمنظور ابداع نظریه بهتری از ساختار اتم با ماکس
بورن[279] کار کرد. این فکر به ذهن هایزنبرگ خطور کرد که بهتر است حالت یک
اتم را با فرکانسهایی که از مشاهده طیفها حاصل میشود نشان دهد. او نظریه خود را
درقالب ریاضیات خاصی پروراند که حاوی فهرستی از اعداد بود. سرانجام بور دریافت که
این روش کاملاً قابل قبول است: ریاضیدانان به چنین فهرستی از اعداد ماتریس[280] میگویند. بورن، که میدید این ایده جواب میدهد، مقالاتی را در
اینمورد برای چاپ فرستاد. درحالی که ایدههای آنها گسترش میافت، نهایتاً این ایدهها
به نوعی ریاضیات پخته و روشمند تبدیل شد که مکانیک ماتریسی نام گرفت. در آن زمان
این نظریه بعنوان رقیبی برای مکانیک موجی شرودینگر دیده میشد.
چه کسی
درست میگفت؟ همانطور که شرودینگر در 1926 کشف کرد، معلوم شد که این دو نظریه در
واقع یکی هستند. آنها یک مفهوم واحد را با دو روش ریاضی مختلف نشان میدادند
(درست مثل روشهای اقلیدسی و جبری، که هر دو تعابیر هندسی یکسانی دارند). در ابتدا
هایزنبرگ نمیتوانست چنین چیزی را باور کند، زیرا رویکرد ماتریسی او حاکی از پرشهای
ناپیوستهای بود که هنگام تغییر حالت الکترون روی میدهد. اجزاء ماتریسهای او با
تغییرات انرژی متناظر بودند. او نمیتوانست ببیند چگونه امواج، که ذاتاً پیوسته
بودند، بتوانند نمایش دهنده پدیدههای ناپیوسته باشند. او در نامهای به فیزیکدان
اتریشی، ولفگانگ پائولی، نوشت: ”هر چه بیشتر در مورد بخش فیزیکی نظریه شرودینگر
فکر میکنم، آنرا زنندهتر مییابم ... به احتمال زیاد آنچه شرودینگر در مورد قابل
تصور بودن نظریهاش میگوید، غلط است، به عبارت دیگر، مشتی چرندیات است.“ ولی
حقیقتاً این اختلاف یادآور یک بحث قدیمی بود که بین اویلر و برنولی، در مورد
جوابهای معادله موجی، در جریان بود. برنولی فورمولی برای حل این معادلات بدست
آورده بود، ولی اویلر نمیتوانست ببیند که چگونه این فرمول، که پیوسته بنظر میرسید،
میتواند جوابی برای یک پدیده ناپیوسته باشد. با این وجود، هم برنولی درست میگفت،
و هم شرودینگر. درست است که معادلات شرودینگر پیوسته هستند، ولی بسیاری از
ویژگیهای جوابهای آنها میتواند ناپیوسته باشد، از جمله سطوح انرژی.
بسیاری از
فیزیکدانان رویکرد مکانیک-موجی را بدلیل اینکه قابل درکتر بود ترجیه میدادند.
ماتریسها جنبه انتزاعیتری داشتند. بااینحال هایزنبرگ ماتریسهای خودش را ترجیه
میداد، زیرا از یکطرف آنها شامل مشاهدات کمّی بودند، و از سوی دیگر بنظر میرسید
که بطور تجربی نمیتوان موجهای شرودینگر را آشکار کرد. در واقع تفسیر کپنهاگی از
نظریه کوانتوم، که بصورت گربه شرودینگر تجسم میشود، حاکی از این است که هرگونه
تلاشی برای انجام اینکار موجب ” فروریزش[281]“ موج میشود. بنابراین برای هایزنبرگ بیشتر
این اهمیت داشت که چه جنبههایی از مکانیک کوانتوم را میتوان اندازه گرفت، و به چه
طریق. شما میتوانید هر یک از اجزاء ماتریسهای او را اندازه بگیرید. ولی اینکار
را حتی برای یک موج شرودینگر هم نمیتوانید انجام دهید. هایزنبرگ این را دلیل
محکمی برای پایبندی به فرمولبندی ماتریسی خود میدانست.
با پیروی
از این خط فکر، او کشف کرد که شما اساساً میتوانید موقعیت ذره را با هر دقتی که
بخواهید اندازه گیری کنید، ولی برای اینکار بهایی هست که باید بپردازید. دلیل آن
هم این است که هر چقدر موقعیت ذره برای شما روشنتر باشد، به همان اندازه در مورد
اندازهحرکت آن کمتر میدانید. برعکس، اگر شما بتوانید با تقریب بسیار زیادی اندازهحرکت
ذره را حساب کنید، آنگاه حساب موقعیت آنرا از دست خواهید داد. همین مسئله در مورد
انرژی و زمان هم مطرح است. شما میتوانید هر یک از آنها را اندازه بگیرید، ولی
درصورتی که بخواهید اندازهگیری شما دقت بالایی داشته باشد، نمیتوانید همزمان
هردو آنها را بدرستی اندازه بگیرید.
این مشکل
ربطی به روش و یا دستگاههای اندازهگیری نداشت؛ این وجه ذاتی نظریه کوانتوم بود.
هایزنبرگ در نامهای که در سال 1927 به پائولی نوشت دلایل خود را بیان کرد.
سرانجام این نامه الهام بخش چاپ مقالهای شد، و نظرات هیزنبرگ به ”اصل عدم قطعیت[282]“ معروف شد. این اصل یکی از اولین نمونههای بود که بر نوعی
محدودیتِ ذاتی در فیزیک دلالت میکرد. نمودنه دیگر این محدودیت، ادعای اینشتین در
مورد سرعت نور بود، که میگوید هیچ چیزی نمیتواند سریعتر از نور حرکت کند.
با ورودش
به دانشگاه لاپزیگ در سال 1927، هایزنبرگ جوانترین استاد در آلمان شد. در 1933،
درست در همان سالی که هیتلر به قدرت رسید، هایزنبرگ برنده جایزه نوبل در فیزیک شد.
این باعث شد تا وی به شخصیت ذینفوذی بدل شود. اشتیاق او به ماندن در آلمان نازی،
موجب شد تا خیلیها تصور کنند که خود وی هم یک نازی است. تا آنجا که محقق است، او
یک نازی نبود. ولی یک میهنپرست بود، و همین موجب شد تا وی را با نازیها همدست
کند و در بسیاری از فعالیتهای آنها درگیر باشد. مدارکی هست مبنی بر این که
هایزنبرگ سعی کرده تا مانع از آن شود که یهودیها را از مناصب دانشگاهی اخراج
کنند، ولی تلاشهای وی بیفایده بوده. در 1937 او متوجه شد که به وی لقب ”یهودی
سفید“ دادهاند و تهدید شد که به اردوگاههای کار اجباری فرستاده شود، ولی پس از
یک سال، توسط هاینریش هیملر که رئیس اس.اس بود، از کلیه اتهامات وارده تبرئه شد.
او در سال 1937 با الیزابت شوماخر، که دختر یک اقتصاددان بود، ازدواج کرد. اولین
فرزندان وی دو قلو بودند، نهایتاً آنها صاحب هفت فرزند شدند.
در طول
جنگ جهانی دوم هایزنبرگ یکی از برجستهترین فیزیکدانانی بود که در برنامه سلاحهای
هستهای آلمان درگیر بودند. درحالیکه همسر و فرزندان او روانه یک خانه ییلاقی در
باواریا شدند، او در راکتور هستهای برلین مشغول بکار بود. نقش او در پروژه بمب
اتمی آلمان خیلی بحث برانگیز بود. هنگامی که جنگ به پایان رسید، او توسط نیروهای
بریتانیایی دستگیر، و نزدیک به شش ماه برای بازجویی در خانهای نزدیکی کمبریج بسر
میبرد. متن بازجوییهای وی، که اخیراً در اختیار عموم قرار گرفته، کمکی به حل این
بحث نکرد. در جایی از این بازجوییها هایزنبرگ میگوید که او تنها به ساختن یک
راکتور هستهای (موتور هستهای) علاقمند بوده و نمیخواسته خود را درگیر ساختن بمب
اتمی کند: ”باید بگویم که من بطور کامل قانع شده بودم احتمال ساخت یک موتور
اورانیومی برای ما وجود دارد، ولی هیچ وقت فکر ساخت یک بمب را نمیکردم، و اعتراف
میکنم که از ته دل خوشحال بودم که کار ما ساختن یک موتور است و نه یک بمب.“ هنوز
هم بر سر صحت ادعاهای وی بحثهای داغی در جریان است.
هایزنبرگ
پس از خاتمه جنگ و رهایی از بازداشتگاه بریتانیاییها، بکار خود درباره نظریه
کوانتوم بازگشت. او در سال 1976 بر اثر ابتلاء به سرطان فوت کرد.

بیشتر
آفرینندگان نظریه کوانتوم از خانوادههای روشفکر آمده بودند، آنها فرزندان اطباء،
وکلا، استادان دانشگاه و از این قبیل بودند. آنها در خانههای گرانقیمت زندگی میکردند،
موسیقی مینواختند، و در فعالیتهای اجتماعی و فرهنگی شرکت میکردند. دوران کودکی
پدیدآورنده انگلیسی مکانیک کوانتوم، با همه اینها فرق داشت. پدرش فردی بود با
روحیاتی عجیب و خودکامه. این روحیات باعث شده بود تا پدرش بصورت شدیدی از والدین
خودش و همینطور از همسر و فرزندانش گریزان باشد. مادرش بیشتر اوقات چنان مورد عطاب
قرار میگرفت که بهمراه دو فرزند خود تنها در آشپزخانه غذا میخورد، در حالیکه شوهر
و پسر کوچکش در تنهایی و سکوت در اطاق غذا میخوردند.
پدرش، که
چارلز آدرین دیراک نام داشت، در سال 1866 در واله سویس بدنیا آمد. او در سن بیست
سالگی از خانه فرار کرد. چارلز در 1890 به بریستول آمد ولی تا سال 1919 هنوز تبعه
انگلستان نشده بود. او در 1899 با فلورانس هانا هولتن، که دختر ناخدای یک کشتی بود،
ازدواج کرد، و سال بعد نخستین پسر آنها بنام رجینالد بدنیا آمد. دو سال بعد، دومین
پسر آنها، پل آدرین موریس، به جمع خانواده اضافه شد؛ چهار سال بعد نیز آنها صاحب
دختری بنام بئاتریس شدند.
چارلز
هنوز به والدین خود نگفته بود که ازدواج کرده، و یا صاحب فرزند شده، تا اینکه در
سال 1905 به ملاقات مادرش در سویس رفت. در آن هنگام از مرگ پدرش ده سال میگذشت.
چارلز
بعنوان معلم در کالج فنی بریستول استخدام شد. او کلاً معلم خوبی بود، ولی به این
معروف بود که خیلی سرد و خشک، و بیش از اندازه پایبند انضباط است. بطور خلاصه، او
آدم سختگیری بود، بااینحال بیشتر معلمان آن دوره همینطور بودند.
این رفتار
پدرش موجب شد تا پل، که طبعاً درونگرا بود، در غیاب هرگونه زندگی اجتماعی، منزویتر
شود. چارلز، ظاهراً برای اینکه او را ترقیب کند تا فرانسوی یاد بگیرد، اصرار داشت
تا پل همیشه به آن زبان با او صحبت کند. بدلیل اینکه فرانسوی صحبت کردن پل افتضاح
بود، او بهتر دید که اصلاً صحبت نکند. در عوض او وقت خود را صرف تفکر درباره طبیعت
میکرد. بنظر میرسد یکی از دلایل غذا خوردن آنها در خلوت، این باشد که کلیه
صحبتها در خانه دیراکها باید تماماً بزبان فرانسوی باشد. هیچ وقت این مسئله روشن
نشد که پل از پدرش متنفر بود، یا فقط از وی خشنود نبود، ولی هنگامی که چارلز مُرد،
گفته اصلی او این بود: ”من حالا احساس آزادی بیشتری میکنم“.
چارلز به
استعدادهای فکری پل افتخار میکرد و نسبت به آینده فرزندانش اشتیاق نشان میداد (یعنی
میخواست آنها همان کاری را دنبال کند که او برای آنان درنظر گرفته بود). وقتی
برادر بزرگتر پل، رجینالد، گفت که میخواهد پزشک شود، چارلز اصرار کرد که او باید
مهندس شود. در 1919، رجینالد یک مدرک مهندسی با نمراتی بسار پایین گرفت؛ پنج سال
بعد، هنگامی که بر روی یک پروژه مهندسی در شهر ولورهامپتون مشغول بکار بود، دست به
خود کشی زد.
پل پیش
والدینش زندگی میکرد، او نیز در همان دانشگاهی که برادرش درس میخواند، به تحصیل
مهندسی پرداخت. موضوع مورد علاقه او ریاضیات بود، ولی تصمیم گرفت که در آن رشته
تحصیل نکند. احتمالاً او نمیخواست برخلاف میل پدرش رفتار کند؛ ولی او به اشتباه
تصور میکرد که تنها شغل ممکن برای کسی که مدرک ریاضی گرفته معلمی است، عقیدهای
که امروز هم رواج دارد. هیچ کس به وی نگفته بود که شغلهای دیگری هم برای این مدرک
وجود دارد، از جمله کارهای تحقیقاتی.
چیزی که
سبب نجات او از این گمراهی شد، سرمقاله روزنامه تایمز در 7 نوامبر 1919 بود، که با
تیتر درشت نوشته بود ”انقلاب در علم، نظریه جدید جهان، واژگونی عقاید نیوتنی“. در
زیر ستون دوم یک تیتر فرعی با این عنوان بچشم میخورد ”فضای خمیده“. به
ناگاه، همه در آن زمان درباره نسبیت حرف میزدند.
بخاطر
دارید که یکی از پیشگوییهای نسبیت عام این بود که گرانش موجب میشود نور 2 برابر
بیشتر از آن مقداری که قوانین نیوتون پیشگویی میکرد خم شود. برای تائید این مسئله
فرانک دایسون و سر آرتور ادینگتون، یک سفر تحقیقاتی را بسوی جزایر پرینسیپه در
آفریقای غربی، که محقق بود در آنجا یک خورشید گرفتگی کامل بوقوع خواهد پیوست، آغاز
کردند. همزمان با آن، اندرو کروملین از رصدخانه گرینویچ هم با گروهی دیگر عازم
سوربال در برزیل شدند. هر دو گروه مشاهده کردند که در مدت زمان گرفتگی کامل، نور
ستارگان دیگری که از کنارههای خورشید دیده میشوند، به مقدار اندکی از موقعیت
ظاهری ستاره، تغییر مسیر دادهاند. و این مسئلهای بود که با نظریه نسبیت تطابق
داشت، و نه با مکانیک نیوتونی.
به یکباره
اینشتین مشهور شد. دیراک برای مادرش یک کارتپستال فرستاد، که در پشت آن نوشته شده
بود ”مادر عزیر، امروز خبرهای مسرتبخشی رسید. اچ.ا لورنتز تلگرافی فرستاده که میگوید
هیئت انگلیسی توانسته انحراف نور بوسیله خورشید را مشاهده کنند. نسبیت مرا هیجانزده
کرده، ما دراینباره خیلی بحث میکنیم. همه دانشجویان دراینباره با هم حرف میزنند،
ولی اطلاعات دقیق اندکی در اینمورد هست.“ دانش عموم از نسبیت، محدود به معنای تحتالفظی
آن بود؛ فیلسوفان ادعا میکردند که از سالها قبل میدانستهاند که ”همه چیز نسبی
است“، و این فیزیک جدید را یک چیز پیشپا افتاده تصور میکردند. متاسفانه، آنها با
این کارشان، تنها نادانی خود را نشان میدادند، و در دامی افتادند که کلمه گمراه
کننده ”نسبیت“ در برابر آنها قرار داد.
پل در
کلاسهایی چارلز بِراد درباره نسبیت شرکت کرد، ولی کلاسهای براد، که استاد فلسفه
بود، محتوای ریاضی اندکی داشت. نهایتاً او نسخهای از کتاب ادینگتون بنام ”فضا،
زمان و گرانش“ را خرید، و ریاضیات و فیزیک لازم برای مطالعه این کتاب را پیش
خودش آموخت. قبل از اینکه او زادگاهش بریستول را ترک کند، او زیر و بم نسبیت خاص و
عام را میدانست.

...........................................
برای ادامه مطالعه این فصل نسخه
کامل PDF کتاب را تهیه کنید.
تا پایان
قرن بیستم، فیزیک به پیشرفتهای فوقالعادهای دست یافته بود. بنظر میرسید که
ساختار جهان در مقیاس کلان بخوبی بوسیله نسبیت عام توضیح داده میشود. پیشبینیهای
قابل توجهای نظیر وجود سیاهچالهها[292] توسط مشاهدات رصدی تائید شدند. از سوی دیگر،
ساختار خُرد جهان، با دقتی بالا و جزئیاتی خارقلعاده، بوسیله نظریه کوانتوم
توضیح داده شد. شکل نوین این نظریه، به نظریه میدانهای کوانتومی معروف است و
نسبیت خاص (و نه عام) را با مکانیک کوانتوم درهم میآمیزد.
ولی با
اینهمه، دو شیطان در این بهشت فیزیکدانان حضور داشتند که موجب میشد تا زیاد هم
این بهشت جای زیبای بنظر نیاید. یکی از این شیاطین ”فلسفی“ بود. به این دلیل
فلسفی، که این دو نظریه کاملاً موفق (نسبیت و کوانتوم)، اساساً (از نظر فلسفی) با
یکدیگر توافقی نداشتند. مفروضات آنها درباره جهان فیزیکی با یکدیگر متناقض بود.
نسبیت عام ”قطعی“ بود - یعنی معادلات آن جایی برای شانس و تصادف باقی نمیگذاشت.
از سوی دیگر بنابر اصل عدم قطعیت هایزنبرگ، نظریه کوانتوم نوعی حالت نامعلومِ ذاتی
داشت، و برپایه این نظر بسیاری از رویدادها، مثل واپاشی یک اتم رادیواکتیو، بصورتی
کاملاً تصادفی روی میدهند. شیطان دیگر ”فیزیکی“ بود. از این نظر فیزیکی، که نظریههای
ذرات بنیادی که بر اصول کوانتومی تکیه داشت چند مسئله مهم را لاینحل باقی میگذاشت،
چیزهای از قبیل اینکه چرا ذرات مختلف جرم خاص خود را دارند، و بویژه اینکه، چرا
اصلاً جرم دارند.
بسیاری از
فیزیکدانان بر این باور بودند که میتوان این دو شیطان را با یک اقدام جسورانه از
بهشت بیرون راند، این اقدام هم چیزی نبود جز متحد کردن نسبیت و نظریه کوانتوم.
یعنی اینکه، نظریه جدیدی ابداع شود که از نظر منطقی منسجم باشد، و از سوی در مقیاس
کلان با نسبیت، و سوی دیگر در مقیاس خُرد با نظریه کوانتوم، تطابق داشته باشد. این
کاری بود که اینشتین نیمی از عمرش را برای حصول به آن تلاش کرد، و ناکام ماند.
فیزیکدانان با فروتنی خاصی به چنین نظریهای نام ”نظریه همه چیز[293]“ را دادهاند، به این امید که تمامی فیزیک آنقدر خلاصه شود که
بتوانیم فرمول آنرا روی یک تیشرت چاپ کنیم.
این یک
ایده غیرواقع بینانه نبود. شما قطعاً میتوانید معادلات ماکسول را روی یک تیشرت
بنویسید. خود من هم یک تیشرت دارم که معادلات نسبیت خاص روی آن نوشته شده، و زیر
آن هم به عبری شعار معروف ”بگذار نور باشد[294]“ چاپ شده. دوستی در فرودگاه تلآویو این تیشرت
را برای من خریده بود. متحد کردن نظریههای مختلف فیزیکی، که بظاهر از یکدیگر جدا
بودند، قبلاً در اقدامات کماهمیتتری انجام گرفته بود. مثلاً الکتریسیته و
مغناطیس، که زمانی تصور میشد دو پدیده متفاوت هستند که از دو نیری کاملاً متفاوت
در طبیعت سرچشمه میگیرند، توسط نظریه ماکسول با یکدیگر متحد شدند و یک پدیده واحد
بنام الکترومغناطیس را بوجود آوردند. این نام که ممکن است کمی عجیب باشند، ولی
بخوبی روند متحدسازی را بازتاب میدهنده. نمونهای از این اتحادها که نسبتاً جدید
است، و غیر از جوامع علمی در کمتر جایی بگوش میرسد، نظریه الکتروضعیف[295] است، که الکترومغناطیس و نیروی هستهای ضعیف را با یکدیگر متحد میکند[296]. اتحاد دیگری هم انجام گرفت که نیروی هستهای قوی را دربرداشت،
ولی یک نیرو از این ترکیب غایب بود، و آنهم چیزی نبود جز گرانش.
با توجه
به این تاریخچه، کاملاً معقول بنظر میرسید که این آخرین نیروی طبیعت نیز با بقیه
فیزیک در یک خط قرار گیرد. متاسفانه، گرانش دارای خصوصیات عجیبی است که این روند
را کند و مشکل ساخته.
این
احتمال هست که ”نظریه همه چیز“ غیر ممکن باشد. اگرچه تاکنون معادلات ریاضی (یا
همان قوانین طبیعت) در توصیف جهان ما موفق بودهاند، ولی هیچ تضمینی نیست که این
روند ادامه یابد. شاید جهان تا آن اندازه که فیزیکدانان تصور میکنند از ریاضیات
پیروی نمیکند و قانونمند نیست.
نظریههای
ریاضی میتوانند بشکل بسیار خوبی جهان را تخمین بزنند، ولی محقق نیست که ریاضیاتی
یافت شود که بصورت کامل بازتابدهنده واقعیت باشد. اگر چنین باشد، آنگاه
به هم بافتن نظریههایی که با یکدیگر سازگاری ندارند ممکن است تقریبهای عملی را
فراهم آورد که در قلمروهای متفاوت اعتبار دارند (و ممکن است هیچ اصل منفردی وجود
نداشته باشد که کلیه این تقریبها را با یکدیگر ترکیب کند و در همه قلمروها معتبر
باشد.)
البته کار
دیگری هم میتوان کرد و آن استفاده از لیست بلند بالایی از قواعد است که شامل
اگر/آنگاهها است: ”اگر سرعتها کم است و مقیاسها کوچک، آنگاه از مکانیک نیوتونی
استفاده کن؛ اگر سرعتها بالا و مقیاسها بزرگ است، آنگاه از نسبیت خاص استفاده کن،
...“ قر و غاتی کردن نظریهها به این شکل بشدت زشت است؛ اگر زیبایی واقعیت
است، آنگاه قر و غاتی کردن فقط میتواند نشانهای از نادرستی باشد. ولی شاید جهان
از ریشه زشت باشد. شاید اصلاً ریشهای نباشد که بر آن رویید. اینها
افکار خوشایندی نیستند، ولی ما در چه جایگاهی قرار داریم که بخواهیم زیباشناسی
کوتهنظرانه خود را به کل جهان تحمیل کنیم؟
دیدگاهی
که میگوید نوعی از ”نظریه همه چیز“ باید وجوداشته باشد یادآور ادیان
یکتاپرستی است، که در آن مجموعهای از خدایان و الهههای ناهمگون، که در طول چندین
هزار سال مورد پرستش انسان بودند، با یک خدای واحد جایگزین شدند که قلمرو
فرمانروایی او همهجا و همهچیز بود. عموماً این روند را بعنوان پیشرفتی در تاریخ
بشر درنظر میگیرند، ولی این مسئله به یک خطای مرسوم فلسفی شباهت دارد که به
”برابری مجهولات“ معروف است، و در آن یک علت را به تمامی پدیدههای ناشناخته نسبت
میدهند. همانطور که نویسنده معروف ایزاک آسیموف[297] گفته بود، اگر شما از چیزهای مثل بشقاب پرنده،
تلهپاتی[298]، و یا اشباح، گیج و آشفته شدهاید، آنگاه بدیهیترین توضیح این
است که آنها را با هم جمع کنید و مثلاً بگویید: ”بشقاب پرندهها توسط اشباحی هدایت
میشوند که قدرت تلهپاتیک دارند!“ با ”توضیحاتی“ نظیر این، انسان نوعی
پیشرفت کاذب را در خود حس میکند (ما قبلاً سه معما داشتیم که باید آنها را توضیح
میدادیم؛ و حالا فقط یکی داریم). ولی این معمای جدید، سه معمای جداگانه را، که
ممکن است توضیحات کاملاً متفاوتی داشته باشند، با هم تلفیق کرده. با این
تلفیق، ما چشم خود را بر روی این توضیحات بستهایم.
وقتی شما
خورشید را بوسیله خدای-خورشید، و باران را با خدای-باران توضیح میدهید، شما
میتوانید به هر خدا صفات ویژه خودش را نسبت دهید. ولی اگر اصرار داشته باشید که هم
خورشید و هم باران توسط یک خدا هدایت میشوند، آنگاه ممکن است در آخر کار مجبور
شوید دو چیز متفاوت را به همدیگر بچسبانید. از برخی جهات فیزیک بنیادی بیشتر شبیه
مذاهب بنیادگرا است (که میتوانیم آنرا فیزیک بنیادگرایان بنامیم). معادلات
روی یک تیشرت جای یک خدای حی و حاضر را میگیرند و آشکار سازی پیامدهای آن
معادلات جای مداخله الهی در زندگی روزمره را.
فارغ از
این تردیدها، من قلباً به بنیادگرایی فیزیکی اعتقاد دارم. من دوست دارم روزی
را ببینم که نوعی ”نظریه همه چیز“ کشف شده باشد، و این نظریه از لحاظ ریاضی زیبا و
درست باشد. فکر میکنم مومنان مذهبی هم ممکن است در این دیدگاه با من شریک باشند،
زیرا آنها میتوانند این را دلیلی بر ذوق و آگاهی بیحد پروردگار خود بدانند.
جستجوی
امروز ما برای نوعی از ”نظریه همه چیز“، ریشه در تلاشهای پیشین دارد که میخواست
الکترومغناطیس و نسبیت عام را (که تمامی فیزیک آن زمان را تشکیل میداد) با یکدیگر
متحد کند. این تلاشها تنها 14 سال پس از ارائه اولین مقاله اینشتین درباره نسبیت
خاص، 8 سال پس از پیشگویی او درباره خم شدن نور بوسیله گرانش، و 4 سال پس از اینکه
نسبیت عام را فرمولبندی کند، انجام گرفت. این تلاش چنان خوب بود که براحتی میتوانست
کلاً مسیر فیزیک را تغییر دهد، ولی بدبختانه کارهای مخترع آن، با چیزی همزمان شد
که بواقع مسیر فیزیک را تغییر داد، و آنهم چیزی نبود جز مکانیک کوانتوم. هنگامی که
همه آبها از آسیاب ریخت، فیزیکدانان دیگر علاقه خود را نسبت به نظریه میدانهای
متحد از دست داده بودند؛ دنیای کوانتوم غنایم با ارزشتری را به آنها نوید میداد، و
شانس بیشتری برای کشفیات مهم در اختیار آنها میگذاشت. شصت سال طول کشید تا ایدههای
پنهان در پشت اولین تلاشها، دوباره احیا شوند.
داستان از
شهر کونیگسبرگ[299]، که در آن زمان پایتخت استان پروس شرقی بود،
شروع شد. حالا این شهر کالینینگراد نامیده میشود و مرکز ناحیه دوری از روسیه است
که میان لهستان و لیتوانی قرار دارد. این شهر تاثیر شگفتانگیزی در پیشرفت ریاضیات
داشت که با یک معما شروع شد. کونیگسبرگ بر روی رودخانه پرگل (حالا پرگولیا) بنا
شده بود و هفت پل، دو طرف این رودخانه، و دو جزیره که در وسط این رود قرار داشت را
به یکدیگر متصل میساختند. آیا مسیری وجود داشت که از طریق آن یک شهروند
کونیگسبرگی بتواند تمام پلها را طی کند ولی هیچگاه دو بار از روی یک پل عبور
نکند؟ یکی از شهروندان کونیگسبرگ، بنام لئونارد اویلر، نوعی نظریه کلی برای این
چنین مسائلی ابداع کرد، و نشان داد که جواب مسئله فوق منفی است، و از آن طریق
اولین قدمها برای بنا نهادن یکی از حوزههای ریاضی، که اکنون توپولوژی[300] نامیده میشود، برداشته شد. توپولوژی درباره آن خواص هندسی بحث میکند
که وقتی شکل خم میشود، تا میخورد، له میشود، و یا هرگونه از شکل افتادگی پیوسته
در آن روی میدهد، آن خواص ثابت بمانند (این از شکل افتادگیهای شامل پاره شدن و یا
بریدن نمیشود).
توپولوژی
به یکی از قدرتمندترین ابزارهای ریاضی امروز بدل گشته، و کاربردهای فراوانی در
فیزیک دارد. این رشته میتواند اشکال ممکن یک فضای چندبعدی را برای ما توضیح دهد.
این مبحثِ روبه گسترشی است که هم در کیهانشناسی، و هم در فیزیک ذرات، مطرح است. در
کیهانشناسی ما میخواهیم شکل فضا-زمان را در مقیاسهای کلان (بعبارتی کل جهان)
بدانیم. در فیزیک ذرات ما میخواهیم شکل فضا و زمان را در مقیاسهای خُرد بدانیم.
شما ممکن است جواب این سئوالات را بدیهی بپندارید، ولی فیزیکدانان دیگر چنین عقیدهای
ندارند، و تردید آنها هم به کونیگسبرگ بازمیگردد.
در سال
1919، ریاضیدان ناشناختهای بنام تئودور کالوزا[301] در دانشگاه کونینگسبرگ نظریه عجیبی را ارائه
داد. او نظر خود را نوشت و آنرا برای اینشتین فرستاد، و ظاهراً او نیز با خواندن
آن سرآسيمه شد. کالوزا راهی را یافته بود که توسط آن میشد گرانش و الکترومغناطیس
را در یک قالبِ واحدِ منسجم، بنام ”نظریه میدانها متحد“، با یکدیگر ترکیب کرد.
این همان چیزی بود که اینشتین برای سالها تلاش میکرد آنرا به سرانجام برساند، ولی
در آن موفقیتی نداشت. نظریه کالوزا خیلی ظریف و طبیعی بود. ولی این اتحاد تنها یک
وجه نارحت کننده داشت، و آن هم این بود که نیاز داشت تا فضا-زمان، بجای چهار بعد،
پنج بعد داشته باشد. بعد زمانی همان بود که همیشه بود، ولی لازم بود که فضا، بشکلی
بجای سه بعد، دارای چهار بعد باشد.
البته
کالوزا قصد نداشت تا گرانش و الکترومغناطیس را با یکدیگر متحد کند. بنا به دلایلی
که فقط خودش خوب میدانست، او درگیر گرانش پنج بعدی شد، شاید نوعی تمرین ریاضی بود
که نشان میداد اگر فضا دارای یک بعد اضافی باشد، آنگاه معادلات میدان اینشتین به
چه صورت درمیآیند.
معادلات
اینشتین در چهار بعد، دارای ده ”مؤلفه“ هستند (یعنی آنها به ده معادله جداگانه
خلاصه میشوند، که هر یک از آنها ده عدد مختلف را توضیح میدهد). این اعداد
بایکدیگر تانسور متریک را تشکیل میدهند، که تشریح کننده انحناء فضا-زمان است. در
پنج بُعد، پانزده مؤلفه، و بنابراین پانزده معادله، وجود دارد. ده تای آنها نظریه
چهار-بعدی متعارف اینشتین را بازتولید میکنند، که البته جای تعجب هم ندارد، زیرا
یک فضا-زمان چهار-بعدی در یک فضا-زمان پنج-بعدی جای میگیرد، و بنابراین شما
انتظار دارید نسخه چهار-بعدی گرانش در نسخه پنج-بعدی آن بگنجد. ولی تکلیف آن پنج
معادله باقیمانده چه میشود؟ آنها فقط میتوانستند حاکی از ساختارهای ویژهای
باشند که ارتباط زیادی با جهان ما ندارد. ولی درعوض، چیزی که موجب شگفتی اینشتین
شد این بود که آنها بسیار آشنا بنظر میرسیدند. چهار تا از معادلات باقیمانده
کالوزا دقیقاً همان معادلات ماکسول برای میدان الکترومغناطیسی بودند، یعنی همان
معادلاتی که در فضا-زمان چهار-بعدی خودمان برقرار است.
تنها
معادله باقیمانده هم تشریح کننده یک نوع ذره بسیار ساده بود که نقش مهمی را ایفا
نمیکرد. ولی هیچکس، حداقل خود کالوزا هم، تصور نمیکرد که هم نظریه گرانش اینشتین
و هم نظریه الکترومغناطیس ماکسول، بصورت خودبخود از گرانش پنج بعدی بیرون بیاید. محاسبات
کالوزا ظاهراً نشان میداد که نور پدیدهای است که از ارتعاشات آن بعد پنهان فضا
بوجود میآید. شما میتوانستید گرانش و الکترومغناطیس را در یک نظریه یکپارچه جای
دهید، فقط باید فرض میکردید که فضا دارای چهار بعد، و فضا-زمان دارای پنج بعد
است.
مقاله
کالوزا برای اینشتین عذاب آور بود، زیرا به هیچ وجه دلیلی وجود نداشت که تصور کنیم
فضا دارای یک بعد اضافی است. ولی هرچقدر هم که این ایده عجیب بنظر میرسید، آنقدر
زیبا و دور از دسترس بود، که نهایتاً او تصمیم گرفت باید چاپ شود. اینشتین بعد از
دوسال دودلی، قبول کرد که مقاله کالوزا در یک نشریه مهم فیزیک چاپ شود. عنوان
مقاله چنین بود ”مباحثی درباره وحدت مسائل فیزیک“.
هر صحبتی
در باره ابعاد اضافی ممکن است مبهم و رمزآلود بنظر برسد. ابعاد اضافی مفهومی بود
که در فرهنگ روحگرایی عصر ویکتوریا رواج داشت، که برطبق آن، بعد چهارم را جایی
برای چیزهایی میدانستند که در زمین جای نمیگرفت. مثلاً، روح از کجا میآید؟
اکتوپلاسم[302] از کجا میآید؟ جواب همه این سئولات بعد چهارم بود. حتی علمای
الهیات نیز خدا و فرشتگانش را در آنجا جای میدادند، ولی بعد متوجه شدند که بعد
پنجم بهتر از چهارم است و ششم بهتر از پنجم، و نهایتاً این مبحث مطرح شد که یک
وجودِ قادرِ مطلق که همیشه حیوحاضر بوده باشد، تنها میتواند در فضایی با ابعاد
بینهایت وجود داشته باشد.
اینها
موضوعات بامزهای بودند، ولی اصلاً مبنای علمی نداشتند. بنابراین، ارزش داشت که
مبنای ریاضی چنین مباحثی روشن شود. نکته اصلی این است که ”ابعاد“ یک دستگاه ریاضی،
یا فیزیکی، شامل تعداد متغیرهای منفردی است که برای تشریح آن لازمند.
دانشمندان
مدت زمان زیادی را صرف فکر درباره متغیرها (کمیتهای قابل تغییر) کردهاند. حتی
دانشمندان تجربی مدت زمان بیشتری را صرف اندازهگیری آنها نمودهاند. ”
بُعد“، که فقط نوعی روشی هندسی برای اشاره به یک متغیر است، آنقدر مفید واقع شد که
حالا جزء لاینفکی از علوم و ریاضیات است. این مفهوم، به روشی مرسوم برای اندیشیدن
بدل شده و حالا کاملاً پیشپاافتاده و عادی محسوب میشود.
زمان یک
متغیر غیرفضایی است، بنابراین میتواند بعنوان بعد چهارم بحساب آید. ولی همین
مسئله درباره کمیتهایی از قبیل دما، سرعت باد، و یا میانگین طول عمر موریانهها
در کشور تانزانیا هم صادق است. موقعیت یک نقطه در فضای سه-بعدی به سه متغیر بستگی
دارد (فواصل آن از شرق، شمال، و بالا نسبت به یک نقطه مرجع). به همین قسم، هر چیزی
که به چهار متغیر بستگی دارد، در یک ”فضای“ چهار بعدی زندگی میکند، و آنچه که به
101 متغیر بستگی دارد، در یک فضای 101 بعدی.
هر دستگاه
مرکبی ذاتاً چند بُعدی است. شرایط آب و هوایی در حیاط خانه شما به عواملی گوناگونی
بستگی دارد: مثلاً دما، رطوبت، سه مؤلفه سرعت باد، فشار بارومتری، شدت بارش باران
(تا اینجا شد هفت بعد)، و یا عوامل متعدد دیگری که ممکن است به این مجموعه اضافه
شود. شرط میبندم که نمیدانستید حیاط شما هفت-بعدی است! وضعیت 9 سیاره (اگر
بخواهیم پلوتو بیچاره را از دور خارج کنیم، 8 سیاره) منظومه شمسی با 6 متغیر (سه
متغیر فضایی و سه مؤلفه سرعت) برای هر سیاره مشخص میشود. بنابراین منظومه شمسی،
یک شی 54 بعدی ریاضی است؛ و البته اگر شما قمرها و سیارکها را نیز به این مجموعه
اضافه کنید، این ابعاد بیشتر هم خواهد شد. در علم اقتصاد ما با میلیونها کالای
مختلف سر و کار داریم، که هر یک از آنها ارزش خاص خود را در اقتصاد یک کشور بازی
میکنند، و یک فضای چند میلیون-بعدی را تشکیل میدهند. در مقابل اینها،
الکترومغناطیس، که برای مشخص کردن حالتهای محلی میدانهای الکتریکی و مغناطیسی
تنها به شش عدد نیاز دارد، اصلاً عددی بحساب نمیآید. مثالهایی مانند اینها
فراوانند. همچنان که علم به سیستمهایی با متغیرهای بالا علاقه نشان میداد، مجبور
شد تا با مفهوم عجیب فضاهای چند بعدی هم روبرو شود.
صورت
ریاضی فضاهای چند بعدی کاملاً جبری است، و برپایه تعمیم مفاهیم ”شناختهشده“ فضا
در ابعاد پائین پی ریزی شده. برای مثال، هر نقطه در صفحه (یک فضای دو-بعدی) میتواند
توسط دو مختصات مشخص شود، و هر نقطه در یک فضای سه-بعدی با سه نقطه مشخص میشود.
بدیهی است که برای تعین یک نقطه در فضای چهار-بعدی به فهرستی با چهار عدد نیاز
است، و بصورتی عمومیتر، برای مشخص کردن یک نقطه در یک فضای n-بعدی، به فهرستی شامل
n مختصات نیاز است.
بنابراین خود فضای n-بعدی
(یا به اختصار فضای- n) تنها یک مجموعه است
که از کلیه این نقاط تشکیل شده.
با
استفاده از تدابیر جبری مشابه، شما خواهید توانست در یک فضای-n، فاصله بین دو نقطه،
زاویه بین دو خط، و غیره را بدست آورید. از آنجا به بعد، مسئله فقط تخیل شما است.
بیشتر اشکال هندسی معمولی 2، یا 3 بعدی، موارد مشابهی نیز در فضاهایی با n بعد دارند، و روش
یافتن آنها از تشریح اشکال مشابه بوسیله جبر در فضاهای 2 یا 3 بعدی، و سپس تعمیم
دادن آن به مختصات n
بعدی است.
بمنظور اینکه فضای n-بعدی را حس کنیم، باید خودمان
را با عینکهای n-بعدی
مجهز کنیم. برای اینکار ما میتوانیم ترفندهایی را اتخاذ کنیم که کشیش و معلم
انگلیسی، ادوین ابوت ابوت [303]، در کتاب خود بنام سرزمینتخت[304]، از آنها استفاده کرد. این کتاب درباره
ماجراهای مربعی است که در یک فضای اقلیدسی 2-بعدی زندگی میکند. این مربع، که
آلبرت نام دارد، هیچ اعتقادی به مفهوم بیمعنی فضای سه بعدی ندارد، تا اینکه در
روزی شوم، یک کره از جهان صفحهمانند او عبور میکند و او را به قلمروی وارد میکند
که هرگز نمیتوانست تصور آن را هم بکند. سرزمینتخت، در قالب یک داستان
اخلاقی درباره بعد چهارم، نوعی نگاه طنزگونه به جامعه ویکتوریایی آن دوران
داشت. آن چیزی که از این کتاب برای ما مفید است جنبههای قیاسی آن است و نه جنبههای
هجوآمیز آن. حال که خود را بعنوان یک موجود دو بعدی در یک صفحه تجسم کردید که از
واقعیات بزرگتری که در بعد سوم در جریان است هیچ اطلاعی ندارد، آنگاه سخت نخواهد
بود که خودتان را همچون موجودی 3 بعدی فرض کنید که هیچ اطلاعی از واقعیات عمیقتر
جهان 4-بعدی ندارد. فرض کنید آلبرت (همان مربع ما)، راحت در سرزمینتخت خود نشسته،
و میخواهد یک کره جامد را پیش خود ”تصور“ کند. ابوت این کار را بوسیله کرهای
انجام میدهد که بصورت عمود از صفحه سرزمینتخت عبور میکند، و آلبرت میتواند
سطح مقطع آنرا ببیند.
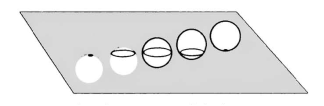
برخورد و عبور یک کره از سرزمینتخت
در ابتدا
او تنها نقطهای را میبیند که بصورت یک دایره در میآید. تاوقتی استوای کره وارد
سرزمینتخت نشده، دایره بزرگتر و بزرگتر میشود، از آن پس کوچکتر و کوچکتر میشود
تا بصورت یک نقطه درآمده و ناگهان ناپدید میشود.
درواقع
آنچه که آلبرت از این دوایر میبیند، بصورت پاره خطهایی مدرج هستند، ولی حس بینایی
وی آنها را بعنوان دوایر تفسیر میکند، درست شبیه موقعی که حس بینایی 3-بعدی ما از
یک تصویر مسطح که در مردمک چشم شکل میگیرد، بعنوان یک شی 3-بعدی برداشت میکند.
بر همین قیاس، ما میتوانیم یک ”ابرکره“، که مشابه
کره معمولی در یک فضای 4-بعدی است، را بصورت نقاطی ”ببینیم“، که ابتدا بصورت
یک نقطه ظاهر میشوند و بعد بصورت کرهای دیده میشوند که به تدریج تا وقتی استوای
ابرکره در فضای ما وارد نشده، قطر آن کره بزرگتر و بزرگتر میشود، تا اینکه پس از
آن کوچکتر و کوچکتر شده و پس از ناپدید میگردد.

برخورد و عبور یک ابرکره از فضای ما
آیا واقعاً
فضا میتواند بیش از 3 بعد داشته باشد؟ منظور من خیالبافیهای صرفاً ریاضی نیست که
با متغیرهای غیرفضایی مرتبطند، بلکه منظورم ابعاد فیزیکی واقعی است؟ چطور
میتوان به بعد چهارم رفت؟
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
در
ماه ژوئن 1972، درست پیش از انتخابات ریاست جمهوری آمریکا، یکی از نگهبانان امنیتی
در مجتمع واترگیت[335] متوجه شد که نوار یکی از درها باز شده. او
که پیش خود تصور میکرد این نوار سهواً بوسیله یکی از کارگران باز گذاشته شده،
نوار را برداشت، ولی هنگامی که بازگشت، متوجه شد که کسی آنرا دوباره بجای خود
گذشته. این باعث شد تا سوء ظن او برانگیخته شود و پلیس را خبر کند. پلیس پنج مرد
را که بصورت غیر قانونی به دفتر کمیته مرکزی حزب دمکرات وارد شده بودند دستگیر
کردند. معلوم شد که این پنج مرد با کمیته انتخاباتی ریچارد نیکسون[336]، که در آن موقع رئیس جمهور وقت آمریکا بود، رابطه داشتند.
این یافتهها
تاثیر اندکی بر روی خود انتخابات داشت، زیرا نیکسون با آراء بالایی انتخاب شد. ولی
داستان فروکش نکرد، و کمکم واقعه واترگیت بر بالاترین سطوح دولت نیکسون اثر
گذاشت. دو خبرنگار روزنامه واشینگتن پست، باب وودوارد[337] و کارل برونشتاین[338]، با جدیت این وقایع را دنبال کردند، و
خبرچینی با نام مستعار ”دیپ تروت[339]“ نیز در این راه به آنها یاری میداد. کسی
هویت واقعی شخص خبرچین را نمیدانست، ولی معلوم بود که باید از مقامات رسمی بلند
پایه باشد. در سال 2005 فاش شد که دیپ تروت شخصی بنام مارک فلت[340] است که در آن زمان معاون اداره افبیآی
بود.
اطلاعاتی
که توسط دیپ تروت به روزنامهها درز کرد مانند توپ صدا کرد. در 1974 نیکسون مجبور
شد از دو تن از دستیاران ارشد خود بخواهد تا استعفا دهند. پس از آن مشخص شد که خود
رئیس جمهور در دفتر خود دستگاههای استراق سمع کار گذاشته، و نوارهایی از گفتگوهای
مهم نیز کشف شد. پس از تلاشهای قانونی که برای دستیابی به این نوارها بعمل آمد،
خلاءهایی در بعضی از این نوارها یافت شد که نشانه پاک کردن عمدی آنها بود.
تلاشهایی
که برای پنهان کردن ورود غیرمجاز به دفتر حزب رقیب و دست داشتن کاخ سفید در آن
انجام گرفت، تقریباً بصورت قریب باتفاق، بعنوان بدترین نوع جرم شناخته شد. مجلس
نمایندگان آمریکا روندی را آغاز کرد که میتوانست به استيضاح رئیس جمهور، و درصورت
گناهکار بودن، نهایتاً به برکناری او منجر شود. هنگامی که محاکمه و استيضاح حتمی
شد، نیکسون استعفا داد.
رقیب
نیکسون در انتخابات سناتور جورج مکگاورن بود. او بعدها در جلسه اعلام
کاندیدتوری خودش برای مجلس چنین اظهار کرد:
”امروزه
دیگر شهروندان ما احساس نمیکنند که بر سرنوشت خود حاکمند. از آن گذشته، مسئله
عمده بیاعتمادی آنها نسبت به رهبرانشان است. جدیدترین اصطلاح در واژگان سیاسی
آمریکا ’شکاف اعتبار‘ است، که همانا فاصله میان گفتار و کردار است. به عبارت
سادهتر، این یعنی که دیگر مردم نسبت به رهبران خود به هیچ وجه اعتماد ندارند.“
درمیان
اعضای کمیته انتخاباتی مکگاورن، یک روزنامهنگار سیاسی بود، که درصورتی که مکگاورن
در انتخابات پیروز میشد، احتمالاً مسیر شغلی وی به سوی دیگری میرفت. شاید در
دنیایی دیگر، سیاست از وجود او غنیتر، ولی فیزیک و ریاضیات پیشرفته، بدون او
بسیار کم رمقتر میبود. در سال 2006، این روزنامهنگار از سوی مجله تایم در
میان یک صد تن از پرنفوذترین افراد سال قلمداد شد، اما در این زمان او دیگر
روزنامهنگار نبود.
در عوض،
نام او بعنوان کسی در فهرست آمده بود که سهم عمدهای در انجام کشفیات نوین در حوزه
ریاضیات و فیزیک داشته. او برای این کشفیات برنده مدال فیلدز[341] شد. فیلدز بزرگترین جایزه در حوزه ریاضیات
محسوب میشود و حکم جایزه نوبل در ریاضیات را دارا است. ولی این شخص فقط ریاضیدان
نیست. او یکی از برجستهترین فیزیکدانان نظری جهان است، و برنده مدال ملی علوم هم
شده. با این همه، اولین مدرک دانشگاهی که وی کسب کرد در رشته تاریخ بود! گرچه او
نخستین بانی اتحاد در فیزیک نیست، ولی از وی بعنوان محرک اصلی و جلودار این حرکت
نام برده میشود. او استاد کرسی فیزیکریاضی در موسسه مطالعات پیشرفته در پرینستون
(همانجایی که اینشتن هم در آنجا کار میکرد) است. این شخص ادوارد ویتن[342] نام دارد.
برخلاف
دیراک بیچاره، ویتن هم مانند برخی از فیزیکدانان آلمانی پیشرو در نظریه کوانتوم،
در محیطی روشنفکر رشد کرد. پدرش لویس ویتن[343]، نیز فیزیکدان است و در زمینه نسبیت عام و
گرانش کار میکند. ادوارد در بالتیمور مریلند بدنیا آمد و نخست برای گرفتن اولین
مدرک خود به دانشگاه برندایس رفت. پس از انتخاب مجدد نیکسون، او به زندگی دانشگاهی
بازگشت، از دانشگاه پرینستون مدرک دکترای خود را گرفت، و در دانشگاههای مختلف
آمریکا شروع به تدریس و تحقیق نمود. او در سال 1987 به سمت استاد در موسسه مطالعات
عالی منصوب شد، جایی که مناصب آن بیشتر بر تحقیقات تمرکز دارد. اکنون هم او در
همین محل مشغول است.
ویتن
تحقیقات خود را با نظریه میدانهای کوانتومی آغاز کرد، نظریهای که حاصل تلاش برای
برقراری آشتی میان نظریه کوانتوم و نسبیت بود. در این نظریه، تاثیرات نسبیتی حرکت
درنظر گرفته میشوند، ولی تنها در فضا-زمانهایی که حالت تخت (مسطح) داشته باشند
(گرانش، که به فضا-زمان خمیده نیاز دارد، مد نظر نیست). در 1998، او طی یکی از
درسهای خود نظریه میدانهای کوانتومی را اینگونه توصیف کرد ”این نظریهای است که
دربردارنده بیشترین دانش ما از قوانین فیزیک است، البته بجز گرانش. این نظریه در
طول هفتاد سال عمر خود، نقطه عطفهای مهمی را به خود دیده، از نظریه پادماده گرفته
... تا توصیف دقیقتر ساختار اتم... تا برسیم به مدل استاندارد ذرات بنیادی.“ او به
این مسئله اشاره میکند که این نظریهها، بدلیل اینکه بیشتر توسط فیزیکدانها بسط
داده شدهاند، دقت ریاضی لازم را ندارند، و به همین جهت تاثیر اندکی بر ریاضیات
گذاشتهاند.
ویتن گفت
که زمان برای جبران این کمبودها مساعد است. بسیاری از حوزههای عمده ریاضیات محض
در واقع چهرههایی از نظریه میدانهای کوانتومی بودند که تغییر قیافه داده بودند.
نقشی که خود ویتن در این راه ایفا کرد، یعنی کشف و تحلیل ”نظریه میدانهای کوانتومی
توپولوژیکی[344]“، دارای تفسیرهای مستقیمی بود که ریاضیدانان بشکل مفاهیم گوناگون،
و در زمینههای مختلف، آنها را ابداع کرده بودند. از جمله آنها، کشف شکوهمند
سیمون دونالدسون[345] درباره فضای چهار-بعدی بود که نشان میداد
این فضا، به لحاظ ساختارهای دیفرانسیلپذیر[346] مختلفی که دارد، یگانه است. جنبههای دیگر
کار او کشفیات مهمی است که اخیراً در نظریه گرهها[347] حاصل شده و به چندجملهایهای جونز شناخته میشود،
و نیز پدیدهای که ”تقارن آینهای“ در سطوح چندبعدی مختلط نامیده میشود، و نیز
چندین حوزه از نظریههای جدید لی.
ویتن یک
پیشبینی جسورانه کرد، و آن این بود که زمینه عمده در ریاضیات قرن بیست و یکم
عبارت خواهد بود از: ادغام ایدههایی که در ”نظریه میدانهای کوانتومی“ مطرحاند
با شاخههای اصلی ریاضیات. او در این باره میگوید:
”در اینجا
یک سلسله جبال طولانی وجود دارد، که بیشتر آن در مه فرو رفته. در نظریههای ریاضی
امروز، تنها قلههای سربفلک کشیده این کوه که از ابرها سر بیرن آورده پیدا است، و
این قلههای باشکوه بصورت جداگانهای از بدنه کوه مطالعه میشوند... بااینحال قسمت
عمده این سلسه جبال هنوز در مه فرو رفته، یعنی همان بدنهای که پایه و اساس آنرا
نظریه میدانهای کوانتومی تشکیل میدهد و حاوی توده عظیمی از گنجینههای ریاضی
است.
درحقیقت
جایزه مدال فیلدز که به ویتن داده شد، به پاس قدردانی از تلاشهای او در کشف برخی
از همین گنجینههای پنهان بود. از میان آنها میتوان به اثبات بهبود یافتهای از
قضیه معروف به ”حدس جرم مثبت[348]“ اشاره کرد که در آن یک سیستم گرانشی با
تراکم جرم موضعی، باید جرم کلی مثبتی را دارا باشد. ممکن است چنین چیزی بدیهی بنظر
برسد، ولی در دنیای کوانتوم، مفهوم جرم موضوع حساسی است. اثبات این قضیه که
فیزیکدانان مدتها بدنبال آن بودند، درسال 1979 توسط ریچارد شواِن[349] و شینگ-تونگ[350] یائو منتشر شد، و باعث شد تا در سال 1982
یائو برنده جایزه مدال فیلدز شود. برهان جدید ویتن، که نوعی اثبات بهبود یافته
برای این قضیه بود، از”ابرتقارن[351]“ بهره میجست، که در نوع خود اولین کاربرد
این مفهوم در یک مسئله عمده ریاضی بود.

ما میتوانیم
مفهوم ابر تقارن را با استفاده از یک معما قدیمی بهتر درک کنیم. این معما میپرسد
که آیا یک درپوش چوبپنبهای وجود دارد که بتوان با آن سر بطریهای مختلفی که
دهانه آنها گِرد، چهارگوشه، و یا سهگوشه باشد را پوشانید. بطور باورنکردنی
چنین اشکالی از چوبپنبه وجود دارد، و پاسخ سنتی به این سئوال این است یک چوبپنبه
با سطح مقطع گرد درست کنید که مانند یک گُوِه باریک شود. اگر از پائین به آن نگاه
شود، مانند یک دایره بنظر میرسد؛ اگر از جلو به آن نگاه شود چهار گوش است؛ از
پهلو که به آن نگاه کنید سه گوش بنظر میرسد. یک شکل منفرد میتواند کلیه این
کارها را انجام دهد، زیرا یک شئ سه-بعدی میتواند ”سایهها“، یا بازتابهای، متعددی
در جهات مختلف داشته باشد.
حالا تصور
کنید یک موجود دو-بعدی بر ”کف“ شکل زیر زندگی میکند. او نیز، بدون اینکه از
بازتابهای دیگر مطلع باشد، قادر است بازتاب چوبپنبه را بر کف زمین خود مشاهد
کند. روزی او در کمال تعجب متوجه میشود که شکل دایرهای به نحو آرامی به مربع
تغییر شکل داده. چگونه چنین چیزی ممکن است؟ مطمئناً چنین چیزی یک تقارن نیست.
بله، در
سرزمین دو بعدی که این موجود زندگی میکند این یک تقارن نیست. ولی در حینی که
موجود دو-بعدی روی خود را برمیگرداند، کسی در فضای سه-بعدی چوبپنبه را طوری میچرخاند
که بازتاب آن روی کف اطاق به مربع تغییر شکل پیدا میکند. و دراینجا باید توجه
داشته باشید که چرخش در فضای سه-بعدی یک تقارن است. بنابراین دربرخی مواقع،
یک تقارن در ابعاد بالاتر میتواند توضیح دهنده یک تبدیل شگفتانگیز در ابعاد
پائینتر باشد.
چگونگی
عملکرد ابرتقارن. شکل سمت چپ: چوبپنبهای که میتواند به سه شکل مختلف سوراخی را
بپوشاند. شکل سمت راست: تاثیر چرخش چوبپنبه.
چیزی شبیه
این نیز در ابرتقارن روی میدهد، با این تفاوت که بجای تغییر دایره به مربع،
فرمیونها به بوزونها تغییر پیدا میکنند. این مورد بسیار شگفتانگیز است. این
یعنی شما میتوانید محاسباتی را با فرمیونها انجام دهید، همه پاسخها را از طریق
ابرتقارن پیدا کنید، و از این طریق، بدون هیچ تلاش اضافی، نتایج را برای بوزونها
استنتاج کنید، و یا بلعکس، شما میتوانید همین کار را برای فرمیونها انجام دهید.
ما انتظار
داریم چنین چیزهایی درمورد تقارنهای واقعی رخ دهد. اگر شما جلو یک آینه بایستید،
و مانند تردستها چند توپ را به هوا پرتاب کنید، آنگاه هر چه در سمتی که شما
ایستادهاید اتفاق میافتد، دقیقاً تعیین کنند آن چیزی است که در آینه اتفاق میافتد.
در آنجا، تصویری از شما وجود دارد که درحال پرتاب توپ هستید. اگر در سمت واقعی،
یعنی سمتی که شما ایستادهاید، پرتاب کردن و گرفتن توپها 3.79 ثانیه طول بکشد، شما
بدون اینکه محاسبهای انجام دهید میدانید که در طرف دیگر نیز 3.79 ثانیه طول میکشد
تا این روند تمام شود. این دو وضعیت توسط تقارن بازتابی با یکدیگر رابطه دارند؛
یعنی آنچه در یکی روی میدهد در دیگری هم روی میدهد، یا بعبارتی بازتاب پیدا میکند.
ابرتقارنها
آنقدرها هم مثل این واضح نیستند، ولی تاثیرات مشابهی دارند. آنها به ما اجازه
میدهند تا خصوصیات یک ذره را از ویژگیهای ذره دیگری استنتاج کنیم، ذرهای که با
اولی کاملاً متفاوت است. این تقریباً مثل این است که شما بتوانید به بعضی از ابعاد
بالاتر جهان بروید، و با چرخاندن یک فرمیون آن را به بوزون تبدیل کنید. ذرات بصورت
جفتهای ابر متقارن میآیند: یک ذره معمولی با ذره تابیده خود، که ابرجفت[352] آن ذره نامیده میشود، وابسته است. الکترونها با سِلکترونها[353] وابستهاند، و کوارکها با سِکوارکها[354]. به جهت برخی دلایل تاریخی، همزاد فوتون
سِفوتون نامیده نمیشود، بلکه نام آن فوتینو[355] است. نوعی ”جهان سایهای“ از ذرات وجود دارد
که تنها بصورت ضعیفی با جهان معمولی تعامل میکند.
این ایده
برای ریاضیات برازنده است، ولی جرم پیشبینیشده این ذرات سایهای آنقدر زیاد است
که نمیشود آنها را در آزمایش مشاهده کرد. ابرتقارن زیباست، ولی ممکن است واقعی
نباشد. گرچه فعلاً تائید مستقیم آن دور از دسترس است، ولی بااینحال تائید
غیرمستقیم آن میسر است. علم عمدتاً نظریهها را از طریق استلزاماتی که از آنها
برمیآید میسنجد.

...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
غرور شیر،
جذبه بلبل، شور چکاوک ... چه صفتِ کلی را باید برای ریاضیدانان بکار برد؟ اگر
بگوئیم ابُهت ریاضیدانان، اینکه زیاد از حد خودبینانه است. اگر بگوئیم سردرگمی
ریاضیدانان، اینکه آنقدر واضح است که نیازی به گفتن ندارد. با توجه به اینکه
فرصتهای فراوانی برای من بوده که رفتار انسان ریاضیدان را، هنگامی که بصورت دسته
جمعی دور هم جمع میشوند از نزدیک مشاهده کنم، فکر میکنم بهترین صفت برای آنها
لغت ”شیدا“ است.
یکی از
این شیدایان، یکی از عجیبترین ساختارها در کل ریاضیات را اختراع کرد، و پی به وجود
اتحاد پنهانی برد که در پشت نمای اسرارآمیز آن قرار داشت. این کشفیات که عمدتاً بر
اثر تفننهای بدون هدف، و ناخواسته حاصل شد، شروع به نفوذ در فیزیک نظری کردند، و
ممکن است کلید برخی از عجیبترین جنبههای نظریه ابرریسمانها باشند.
ریاضیات
ابرریسمانها چنان جدید است که بسیاری از جنبههای آن هنوز اختراع نشده. ولی
ریاضیدانان و فیزیکدانان، بطور طعنهآمیزی، جدیداً کشف کردهاند که ابرریسمانها،
یعنی پیشروترین وجه از فیزیک نوین، ظاهراً ارتباط عجیبی با یک جبر مربوط به قرن
نوزدهم دارند. مبحثی که چنان از مُد افتاده بود که حتی در دروس دانشگاهی هم توجهی
به آن نمیشد. این حوزه از جبر ”اوکتونیونها[403]“ نام دارد، و ساختاری است که در انتهای
فهرست ”اعداد حقیقی، اعداد مختلط، کواترنیونها...“، پس از کواترنیونها قرار میگیرد.
شخصی در
سال 1843 اوکتونیونها (یا هشتگانها) را کشف کرد. در سال 1845 بوسیله شخص دیگری
معرفی شدند، و سپس حتی اعتبار اختراع آن هم بطور اشتباهی به شخص دیگری داده شد،
ولی چون کسی متوجه نشد، اهمیت چندانی هم نداشت. اوکتونیونها تا اوایل قرن بیستم
زیاد شناخته شده نبودند. در سال 1925، هنگامی که فون نیومان و وینگر تلاش کردند تا
آنها را پایه مکانیک کوانتوم قرار دهند، برای مدتی دوباره احیاء شدند، ولی هنگامی
که این تلاشها به شکست انجامید، آنها دوباره به فراموشی سپرده شدند. در دهه 1980
بعنوان ابزارهای که میتوانست در نظریه ریسمانها مفید باشند، دوباره سر کله آنها
پیدا شد. در سال 1999، آنها بعنوان اساسیترین بخش از نظریه 10 و 11 بعدی
ابرریسمانها شناخته شدند.
اوکتونیونها
به ما میگویند که چیز بسیار عجیبی در مورد عدد 8 وجود دارد، و حتی از آن هم
عجیبتر، چیزهایی درباره فیزیکِ فضا، زمان، و ماده وجود دارد که با این عدد ارتباط
دارند. چیزی که تنها یک تفنن ساده و قدیمی بود، دوباره از نو احیاء شد، ولی اینبار
بعنوان کلید حل ژرفترین معماهای ریاضیات و فیزیک پیشرو مطرح میشد، علیالخصوص این
معما که تعداد ابعاد فضا-زمان ممکن است بیش از چهار بعد مرسوم باشد، و به همین جهت
است که گرانش و نظریه کوانتوم میتوانند با هم متحد شوند.

داستان
اوکتونیونها، به قلمرو خروشان جبر مجرد[404] باز میکرد، و موضوع یک تحقیق ریاضی بسیار
زیباست که در سال 2001 توسط ریاضیدان آمریکایی جان بایز[405] انجام گرفت. من شخصاً خیلی تحت تاثیر نگرش
بایز قرار گرفتم، و حداکثر تلاش خود را خواهم کرد تا این جنبههای عجیب، ولی درعین
حال زیبا، که حدفاصل ریاضیات و فیزیک هستند را برای شما بیان کنم. بمنظور سادهتر
کردن بحث، بیشتر عملیات ریاضی از چشم شما پنهان خواهد بود. حوصله داشته باشید، و
از اصطلاحات گنگی که من در اینجا بکار میبردم خیلی نگران نشوید.
برخی از
مطالبی که قبلاً ذکر شد میتواند در اینجا مفید باشد. چیزی که زیر و بم داستان ما
برای تقارن را تشکیل میدهد، گسترش تدریجی دستگاههای اعداد است. اولین مرحله از
این روند، کشف (یا اختراع) اعداد مختلط در اواسط قرن شانزدهم بود. اعداد مختلط
اعدادی هستند که در آن (1-) دارای جذر است. تا پیش از آن، ریاضیدانان تصور میکردند
که اعداد چیزهایی منحصربفرد و خدادادی هستند. به ذهن هیچ کس خطور نمیکرد که عدد
جدیدی را اختراع کند. ولی در حدود سال 1550، کاردانو و بامبلی، با در نظر گرفتن
جذر برای اعداد منفی، اینکار را به ثمر رساندند. حدود 400 سال طول کشید تا مشخص
شود معنی واقعی این اعداد چیست. ولی در طول این مدت، تنها 300 سال کافی بود که
ریاضیدانان قانع شوند که این اعداد مفید هستند و نباید آنها را نادیده گرفت.
در اوایل
قرن نوزدهم، ترکیب ناموزونی که کاردانو و بومبلی اقتباس کرده بودند، به نوع جدیدی
از اعداد تغییر شکل پیدا کرد، که برای نمایش آنها از علامتi استفاده میشد. ممکن است اعداد مختلط عجیب بنظر
برسند، ولی مشخص شده که آنها ابزارهای خارقالعادهای برای فهم فیزیکِ ریاضی
هستند. مسائلی همچون گرما، نور، صوت، ارتعاشات، کشسانی، گرانش، مغناطیس،
الکتریسیته، و جریان سیالات، همگی در برابر سلاحی بنام اعداد مختلط تسلیم میشوند-
اما فقط برای فیزیکی که 2 بُعد دارد.
ولی جهان
ما دارای 3 بعد است، یا بهتر بگویم، تا این اواخر ما به غلط اینطور فکر میکردیم.
بدلیل اینکه دستگاه اعداد مختلط برای فیزیک دو بعدی بسیار کار آمد بود، فیزیکدانان
به این فکر افتادند که شاید مشابه سه بعدی این اعداد هم وجود داشته باشد تا بتوان
از آن برای بررسی پدیدههای فیزیکی واقعی، که در سه بعد اتفاق میافتند، استفاده
کرد. همیلتون سالها تلاش کرد که چنین دستگاهی از اعداد را پیدا کند، ولی در این
راه ناکام ماند. پس از آن در اکتبر 1843، ناگهان فکری به ذهن او خطور کرد: ”جستجوی
خود را به سه بعد محدود نکن، بعد چهارم را جستجو کن“، و پس از آن بود که
معادلات کواترنیونها را بر روی سنگ ورودی پُل بورگهام حک کرد.
همیلتون
یک دوست قدیمی بنام جان گراوِز[406] داشت که از زمان دانشجویی خود با وی آشنا
بود. او در جبر مهارت زیادی داشت. احتمالاً همین گراوز بود که از ابتدا باعث شد تا
همیلتون درمورد گسترش دستگاه اعداد تشویق شود. همیلتون، در همان روزی که پُل را
خراب کرد، نامه مفصلی برای دوستش درباره کواترنیونها فرستاد. گراوز ابتدا گیج شده
بود، و از این متعجب بود که این مسئله تا چه حد میتواند درست باشد که قوانین
جدیدی برای ضرب اختراع کرد. او در جواب همیلتون نوشت ”من هنوز هیچ تصور روشنی
ندارم که ما چقدر اختیار داریم تا نوعی از اعداد موهومی را خلق، و به آنها خواص
غیرطبیعی اهدا کنیم.“ ولی در عین حال او در پشت این مسئله ایدههای بالقوه جدیدی
را میدید و میخواست بداند تا کجا میشود آن را تعمیم داد: ”اگر شما با قدرت
کیمیاگری خود قادرید 3 کیلو طلا درست کنید، چرا به همین اندازه بسنده کنید؟“
این سئوال
خوبی بود، و گراوز میخواست به آن پاسخ دهد. در طی دو ماه او نامهای نوشت و گفت
که یک دستگاه 8-بعدی اعداد را پیدا کرده. او آنها را ”اُکتاو[407]“ نامید. چیزی که در مورد این اعداد
وجود داشت، یک فرمول قابل توجه در مورد مجموع هشت مجذور بود، که من بزودی به آن
بازمیگردم. او سعی کرد که یک دستگاه اعداد 16-بعدی را هم تعریف کند، ولی بقول
خودش ”به یک مانع غیرمنتظره“ برخورد کرد. همیلتون گفت که کمک میکند تا اکتشافات
دوستش در معرض توجه عموم قرار گیرد، ولی او خودش را بیش از اندازه درگیر
کواترنیونها کرده بود، و نمیتوانست اینکار را انجام دهد. پس از آن، گراوز متوجه
نکتهای شد که میتوانست موجب شرمساری باشد: ضرب اوکتانها از قانون شرکتپذیری
پیروی نمیکرد. یعنی برای ضرب سه اوکتان در یکدیگر، (ab)c و a(bc) ، که درمورد دیگر دستگاههای اعداد با هم برابراند، در
مورد اوکتانها معمولاً با هم متفاوتند. همیلتون پس از سالها تامل خودش را
راضی کرده بود که قانون جابجای را کنار بگذارد، ولی صرف نظر کردن از قانون شرکت
پذیری ممکن بود زیاده روی بیش از حد باشد.
در این
زمان گاروز بدشانسی آورد. پیش از آنکه وی مقاله خود را چاپ کند، کایلی[408] مستقلاً همین کشفیات را انجام داد، و در 1945 یافتههای خود را
ضمیمه مقاله دیگری کرد که در مورد توابع بیضوی[409] بود. کایلی بود که به این دستگاه اعداد نام
اوکتونیون را داد.
گراوز از
اینکه نتوانسته بود زودتر مقاله خود را چاپ کند ناراحت بود. گذشته از این،
قرار بود مقاله او نیز در همان نشریهای که کایلی کشف خود را اعلام کرده بود چاپ
شود. بنابراین گاروز یادداشتی ضمیمه مقاله خود کرد و در آن توضیح داد که او 2 سال
قبل به این نظریه دست یافته، و همیلتون نیز طی یادداشت کوتاهی ادعای دوستش را
تصدیق کرد، و یاد آور شد که باید اعتبار این کشف به وی داده شود. گرچه مدارک
تاریخی بخوبی ثبت شده بود، ولی اوکتونیونها خیلی زود نام ”اعداد کایلی“ را بر
خود گرفتند، نامی که هنوز هم بصورت گستردهای بکار میرود. حالا بسیاری از
ریاضیدانان همان اصطلاح کایلی را بکار برده و این اعداد را ”اوکتونیون“ مینامند،
ولی اعتبار کشف آن را به گاروز میدهد. اوکتونیون در مقایسه با اکتاو نام مناسبتری
است، زیرا تا حدی به لغت کواترنیون شباهت دارد.
جبر
اوکتونیونها را میتوان بصورت نمودارِ قابل توجهی که به صفحه فانو[410] معروف است نمایش داد. این نمودار یک هندسه متناهی[411] است که متشکل از هفت نقطه است که توسط هفت خط به هم متصل میشوند.
صفحه فانو، هندسهای متشکل از 7 نقطه و هفت
خط.
بمنظور
اینکه یکی از این خطوط را بتوان در صفحه رسم کرد، باید بصورت دایره خم شود، ولی
این اهمیت چندانی ندارد. در این هندسه، هر دو نقطه بوسیله یک خط بهم متصل میشوند،
و هر دو خط در یک نقطه بهم میرسند. هیچ خطوط موازی وجود ندارد. صفحه فانو بمنظور
کاملاً متفاوتی ابداع شده بود، ولی معلوم شد که دربردارنده قواعد ضربی اوکتونیونها
است.
اوکتونیونها
دارای هشت یکا[412] هستند: عدد معمولی 1، و هفت یکای دیگر که e7, e6, e5, e4, e3, e2, e1,
نامیده میشوند. مجذور هریک از این eها 1- است. نمودار فانو، قواعد ضرب برای
یکاها را تعیین میکند. فرض کنید شما میخواهید e3 را در e7 ضرب کنید. به نقاط 3
و 7 در نمودار نگاه کنید و خطی که آنها را به متصل میکند پیدا کنید. روی این خط،
نقطه سومی هست، که در اینجا این نقطه 1 است. جهت پیکانها را دنبال کنید، شما از 3
به 7 و از آن به 1 میروید، بنابراین حاصل ضرب e3e7=e1
خواهد بود. اگر بخواهید ترتیب آنها را با هم عوض کنید، یک علامت منفی به حاصل
اضافه کنید: پس e7e3=-e1
خواهد بود. اگر همین کار را برای کلیه جفتهای انجام دهید، آنگاه شما خواهید دانست
که چگونه اوکتونیونها را در یکدیگر ضرب کنید. (جمع و تفریق همیشه آسان است، تقسیم
هم توسط ضرب تعیین میشود.)
گاروز و
کایلی چیزی در مورد ارتباط هندسه متناهی با ضرب اوکتونیونها نمیدانستند،
بنابراین مجبور بودند برای آنها یک جدول ضرب تشکیل دهند. صفحه فانو بعدها کشف شد.
برای
سالها اوکتونیونها صرفاً از جنبه کنجکاوی بررسی میشدند. آنها برخلاف کواترنیونها
هیچ تعبیر هندسی، و یا هیچ کاربردی در علوم نداشتند. حتی در حوزه ریاضیات محض هم
بنظر نمیرسید چیزی جالبی از آنها بیرون بیاید. جای تعجب نبود که آنها به فراموشی
سپرده شوند. ولی با دانستن اینکه اوکتونیونها منبع عجیبترین ساختارهای جبری
هستند که تاکنون در ریاضیات شناخته شده، این وضعیت تغییر. اوکتونیونها توضیح میدهند
که منشاء پنج گروه استثنایی لی، یعنی G2,
F4, E6, E7, E8 ،
از کجاست. و گروه E8،
یعنی بزرگترین گروه استثنایی لی، 2 بار در گروه تقارنی ظاهر میشود که نظریه
10-بعدی ریسمانها بر پایه آن قرار دارد. نظریهای که بطور غیر معمولی خواص خوشآیندی
را در خود دارد و از نظر بسیاری از فیزیکدانان، فعلاً بهترین کاندید برای یک
”نظریه همه چیز“ بحساب میآید.
اگر ما
قول دیراک که میگوید ”ریشه جهان در ریاضیات است“ را قبول کنیم، آنگاه میتوانیم
بگوییم که ممکن است نوعی از ”نظریه همه چیز“ وجود داشته باشد، زیرا گروه E8 وجود دارد، و دلیل
وجود E8 نیز اوکتونیونها است. این مورد، یک امکان فلسفی فریبنده را در مقابل ما قرار
میدهد: ساختار زیربنایی جهان ما، که میدانیم بسیار خاص است، برحسب رابطهای که
با یک شئ منحصر به فرد ریاضی بنام اوکتونیون دارد، انتخاب شده.
زیبایی
واقعیت است، و واقعیت هم زیبا. اگر فیثاغورثیان و افلاطونیان میدیدند که گواهی
اینچنین برای تائید نظرات آنها پیدا شده که در آن الگوهای ریاضی نقش محوری در
ساختار جهان برعهده دارند، بسیار خرسند میشدند. اوکتونیونها دارای یک زیبایی
فراواقعیِ[413] فراموشنشدنی هستند، که اگر دیراک زنده بود آنرا دلیلی بر درستی
نظریه 10-بعدی ریسمانها میدانست. بدبختانه اگر هم نادرستی این مسئله اثبات شود،
باز هم آنها به همان اندازه چیزهای درست، برای خودشان جذابیت دارند. ولی ما یاد
گرفتهایم که الزاماً قرار نیست که نظریههای زیبا حتماً درست باشند، و تا آن زمان
که هم که رای به نفع نظریه ابرریسمانها صادر نشده، باید در نظر داشت که همه اینها
فقط بصورت یک گمانه زنی محض باقی میماند.
اهمیت
آنها در فیزیک هر چه باشد، آنچه که درباره اوکتونیونها مطرح است برای ریاضیدانان
حکم طلای ناب را دارد.

رابطه بین
اوکتونیونها و گروههای لی استثنایی تنها یکی از روابط عجیبی است که مابین تعمیمهای
مختلف کواترنیونها و فیزیک پیشرو امروزی وجود دارد. من قصد دارم تا آنجایی که
امکان دارد این روبط را برای شما توضیح دهم، تا شما نیز ارزش بیمانند آنها را درک
کنید. من کار خود را با یکی از قدیمیترین ساختارهای استثنایی در ریاضیات، که
فرمول جمع دو مربع است، شروع میکنم.
...........................................
برای ادامه مطالعه این فصل نسخه کامل PDF کتاب را تهیه کنید.
آیا کیتس[449] درست میگفت که زیبایی واقعیت است، و واقعیت هم زیبا؟
احتمالاً
بدلیل اینکه ذهن ما بطور یکسانی به هر دو آنها واکنش نشان میدهد، این دو بطور
نزدیکی با یکدیگر رابطه دارند. ولی آنچه در ریاضیات برقرار است لازم نیست در فیزیک
نیز همینطور باشد، و یا بلعکس. رابطه بین ریاضیات و فیزیک عمیق، ظریف، و
متحیرکننده است. این که چگونه علم ”قوانین“ ظاهری جهان را هویدا میکند، و اینکه
چرا بنظر میرسد جهان به زبان ریاضیات سخن میگوید، هر دو از بغرنجترین معماهای
فلسفی بشمار میروند.
آیا ریشه
جهان ریاضی است؟ آیا جنبههای ظاهراً ریاضی آن صرفاً اختراع بشر است؟ یا اینکه
جهان به این دلیل ریاضی بنظر میرسد که ریاضیات تنها جنبهای از این جهان بینهایت
پیچیده است که ما قادر به درک آن هستیم؟
آنگونه که
برخی تصور میکنند، ریاضیات نسخه کاملاً مستقلی از یک حقیقت غایی نیست. اگر چیزی
از داستان ما برآمده باشد این است که ریاضیات بوسیله انسانها بوجود آمده. ما به
آسانی میتوانیم پیروزیها و محنتهای آنها را مشاهده کنیم. چه کسی میتواند از
جوانمرگ شدن آبل و گالوا در سن 21 سالگی متاثر نشود؟ یکی از آنان بسیار محبوب بود
و تنها گناهش این بود که آنقدر پول نداشت تا ازدواج کند؛ دیگری بااستعداد و بیثبات
بود. ناکام در عشق و رانده شده، شاید علت مرگش نیز همان عشق بود. پیشرفتهای پزشکی
امروز میتوانست آبل را نجات دهد، و شاید حتی بتواند به کسی مانند همیلتون نیز کمک
کند تا اعتیاد به مشروب را ترک کند.
بدلیل
اینکه ریاضیدانان انسانند و مانند بسیاری یک زندگی عادی دارند، فرایند ساخت یک
ریاضیات جدید نیز تا حدی متاثر از روندهای اجتماعی است. ولی آنگونه که نسبیتگرایان
اغلب ادعا میکنند، نه ریاضیات و نه علم، هیچکدام بطورکامل زایده روندهای اجتماعی
نیستند. هر دو آنها به قیودی مقید هستند: در مورد ریاضیات این قید منطق است، و
درمورد علم، آزمایش. هرچقدر هم که ریاضیدانان بیچاره سعی کنند که زاویه را با
روشهای اقلیدسی به سه قسمت تقسیم کنند، حقیقت این است که این کار منطقی نیست و غیر
ممکن است. هرچقدر هم که فیزیکدانان بخواهند جهان را تنها با قانون گرانش نیوتون
توضیح دهند، این کار غیر ممکن است، زیرا از نظر تجربی، حرکت حضیض خورشیدی عطارد
خلاف این را نشان میدهد.
به همین
دلیل است که ریاضیدانان بطور سرسختانهای منطقیاند، و درگیر مسائلی هستند که
بیشتر مردم اهمیتی به آنها نمیدهند. برای مثال آیا واقعاً اهمیتی دارد
که شما بتوانید معادلات درجه پنجم را بوسیله رادیکالها حل کنید؟
جواب
تاریخ به اینچنین سئوالی صریح و قاطع است: آری، این مسائل اهمیت دارند. ممکن است
مستقیماً برای زندگی روزمره ما مهم نباشند، ولی مطمعناً برای جامعه بشری، بصورت
کل، اهمیت دارند. البته نه از این لحاظ که چیز مهمی در حل معادلات درجه پنجم نهفته
است، بلکه درک ما از علت این ناتوانی باعث میشود تا دریچه پنهانی را بسوی یک
ریاضیات جدید باز کنیم. اگر گالوا و پیشگامان دیگر، خود را درگیر فهم این مسئله
نمیکردند که چرا نمیتوان معادلات درجه پنجم بهبالا را با رادیکالها حل کرد،
کشف نظریه گروهها بوسیله انسان بسیار طولانیتر میشد، و شاید هم اصلاً اتفاق نمیافتاد.
شما ممکن
است در آشپزخانه خود، و یا هنگام رانندگی، هیچگاه با مسائلی مثل نظریه گروهها روبرو
نشوید، اما بدون وجود آنها غنای علم بسیار کمتر، و زندگی ما با آنچه که اکنون هست
بسیار متفاوت بود. هیچ کسی نمیتوانست پیشبینی کند که یک سئوال فضلفروشانه
درباره معادلات میتواند عمیقترین ساختارهای جهان مادی را آشکار کند، ولی درواقع
این اتفاقی بود که رخ داد.
پیام
تاریخ ساده و روشن است. به صرف اینکه بنظر میرسد چیزی کاربرد عملی مستقیمی ندارد،
نباید تحقیق بر روی ساختارهای ژرف ریاضی مربوط به آن را رد کرد، یا به حاشیه راند.
ارزش ریاضیات خوب از طلا هم بیشتر است، این مسئله که سرچشمه اینگونه ریاضیات از
کجاست، سخن نامربوطی است. چیزی که بحساب میآید این است که این ریاضیات به چه
چیزهایی منجر خواهد شد.
مسئله
حیرتآور این است که ریاضیات خوب معمولاً از جاهایی نشئت میگیرد که اصلاً انتظار
آن نمیرود، و برخلاف اینکه در ابتدا برای مقاصد کاملاً متفاوتی اختراع شده، بعداً
چنان کاربردی در علوم و فنآوری پیدا میکند که برای آنها جنبه حیاتی دارد. بیضی،
که بعنوان یکی از مقاطع مخروطی توسط یونانیان مورد مطالعه قرار گرفته بود، به
کلیدی بدل شد که نسل به نسل تکامل پیدا کرد و بواسطه کسانی مانند تیکو براهه،
کپلر، و نهایتاً نیوتون، به قانون جاذبه عمومی منتهی شد. نظریه ماتریسها، که کاشف
آن آرتور کایلی برای بیفایده بودن آنها عذرخواهی کرد، به چنان ابزار مهمی بدل شد
که بدون وجود آنها آمار، اقتصاد، و تقریباً کلیه رشتههای علوم، کلاً کارکرد خود
را از دست میدهند. اوکتونیونها ممکن است الهام بخش نوعی از نظریه همه چیز باشند.
البته ممکن است بعداً مشخص شود که نظریه ابرریسمانها تنها یک قطعه زیبای ریاضی
است که کاربرد روشنی هم در فیزیک نداشته باشد. اگر چنین باشد، هر چند این تنها یک
نظریه بوده که برای پاسخ گویی به یک سئوال در ریاضیات محض اختراع شده، بااینحال
کاربرد فعلی تقارن در نظریه کوانتوم هنوز هم نشان میدهد که نظریه گروهها بینش
عمیقی برای ما نسبت به جهان فراهم میآورد.
فیلسوف
یونانی افلاطون میگفت ”خداوند همیشه در حال هندسه بازی است.“ گالیله نیز چیزی شبیه
این گفته بود: ”کتاب بزرگ طبیعت به زبان ریاضیات نوشته شده.“ یوهان کپلر میخواست
نوعی الگوی ریاضی را در مدار سیارات پیدا کند. برخی از آنها نیوتون را به سمت
قانون جاذبه هدایت کرد؛ برخی دیگر هم مهملات عرفانی بود.
بسیاری از
فیزیکدانان عصر نوین درباره قدرت حیرتآور اندیشه ریاضی سخن گفتهاند. ویگنر از
”کارکرد بیحساب ریاضیات“ بعنوان راهی برای درک جهان یاد میکند. جملات او در
عنوان مقالهای که در 1960 نوشت آمده. در متن مقاله، او به چند نکته عمده اشاره میکند:
”اولین
نکته این است که کاربرد شگرف ریاضیات در علوم آنقدر اسرار آمیز است که هیچ توضیح
معقولی نمیتوان برای آن ارائه کرد. دوم اینکه، همین فایده غیرطبیعی مفاهیم ریاضی
است که این سئوال را در برابر ما قرار میدهد که آیا نظریههای فیزیکی ما منحصر
بفرد هستند؟
[1] - Evariste Galois
[2] - Theory of Everything
[3] - transformation
[4] - group
[5] - calculus of symmetry
[6] - quaternion
[7] - octonion
[8] - exceptional Lie groups
[9] - abstract algebra
[10] - Lie group
[11] - theory of superstrings
[12] - Nineveh, Nimrud, Nippur, Uruk, Lagash, Eridu, Ur
[13] - Babylon
[14] - Sargon of Akkad
[15] - zodiac
[16] - Nabu
[17] - shekel، واحد پول بابل قدیم. (مترجم)
[18] - (calculus) همانظور که در مقدمه کتاب آمده، منظور نویسنده از این
نوع حسابان نظریه گروهها است. (مترجم)
[19] - Claudius Rich
[20] - در ایران باستان این دوره تقریباً با سلطنت مادها شروع میشود و
تا ظهور هخامنشان پایان مییابد. (مترجم)
[21] - Seleucid
[22] -Nabu Shamash. شَمش معادل لغت عبری شِمِش، و لغت عربی شَمس، بمعنای
خورشید است. (مترجم)
[23] - Ishtar Gate
[24] - مردوک (Marduk) معروفترین خدای بابل باستان. (مترجم)
[25] - decimal
[26] - این مورد بیشتر در آثار اروپاییها و مخصوصاً ساختههای BBC بچشم میخورد و مثلاً اگر فیلم آنها ساخت سال 2012 باشد بجای اینکه در
آخر تیتراژ فیلم بنویسند 2012، معادل رومی آن یعنی (MMXII)
را مینویسند. (مترجم)
[27] - Otto Neugebauer
[28] - linear
[29] - Siwa
[30] - Amun. ابر خدای مصریان
باستان، معادل زئوس یونانی و ژوپیتر رومیان. (مترجم)
[31] - Re
[32] - Alexander
[33] - Pausaruas
[34] - Mareotis
[35] - Alexandria
[36] - Elements of Geometry
[37] - Elements
[38] - Homer حماسه نویس معروف یونانی. (مترجم)
[39] - Nicolas Bourbaki یا نیکولا بورباکی.
نام مستعار مشترک تعدادی از ریاضیدانان، عمدتاً فرانسوی، بود که در نیمه اول قرن
بیستم بصورت ناشناس، و تحت نام نیکولا بورباکی، کتابهای پیشرفته ریاضی منتشر
میکردند. این کتابها تاثیر
عمیقی بر ریاضیات و آموزش آن برجا گذاشت.
[40] - Proclus
[41] - Eudoxus
[42] - Theaetetus
[43] - (Antikythera) این دستگاه، که
ساختار نسبتاً پیچیدهای دارد و از تعداد زیادی چرخ دنده تشکیل شده، به کامپیوتر
2000 ساله معروف است. (مترجم)
[44] - axiom
[45] - theorems
[46] - constructions
[47] - quadrattrix
[48] - Edward Fitzgerald
[49] - conic sections
[50] - Heron
[51] - Diophantus
[52] - Polygonal numbers
[53] - Fermat's last theorem
[54] - Pierre de Fermat
[55] - Andrew Wiles
[56] - Apollonius of Perga
[57] - inverse square law
[58] - Tartaglia
[59] - Girolamo Cardano
[60] - Jerome Cardan
[61] - Fibonacci
[62] - Fibonacci sequence
[63] - Luca Pacioli
[64] - Morris kline (1992-1908) ریاضیدان و مورخ آمریکایی.
[65] - Leonardo da Vinci (1519-1452).
نقاش، مهندس، موسیقیدان و دانشمند ایتالیایی. وی یکی از شاخصترین هنرمندان و
دانشمندان عصر رنسانس بحساب میآید. (مترجم)
[66] - Pavia and Piatti Foundation
[67] - Lucia Bandarini
[68] - Scipione del Ferro
[69] - Lodovico Ferrari
[70] - Annibale del Nave
[71] - E. Bartolotti
[72] - Jains. جین نوعی آيين هندي است كه با آيين بودا تشابه دارد و رياضت كشي و احترام به همه ي موجودات را تاكيد مي كند. (مترجم)
[73] - Rafaele Bombelli. (1572-1526) ریاضیدان
ایتالیایی و اولین شخصی که به مفهوم اعداد موهومی پی برد. (مترجم)
[74] - Carl Friedrich Gauss
[75] - Brunswick
[76] - Wolfgang Bolyai (1776-1856)
[77] - law of quadratic reciprocity
[78] - Leonhard Euler
[79] - Disquisitiones Arithmeticae
[80] - Johann Pfaff (1765-1825)
[81] - Carl Gustav Jacob Jacobi (1804-1851)
[82] - Fundamental Theorem of Algebra
[83] - Ceres
[84] - Alexander von Humboldt (1769-1859)
[85] - Pierre-Simon de Laplace (1749-1827)
[86] - Johanna Osthoff
[87] - János Bolyai (1802-1860)
[88] - Nikolai Ivanovich Lobachevsky (1792-1856)
[89] - geodesics
[90] - metric
[91] - Hliotrope
[92] - Wilhelm Weber (1804-1891)
[93] - Georg Bernhard Riemann (1826-1866)
[94] - manifolds (به مانیفولد بسلا و چندلا هم میگویند )
[95] - Joseph Louis Lagrange
[96] - Alexandre-Théophile Vandermond
[97] - Giuseppe Lodovico Lagrangia
[98] - Jean le Rond D'Alember (1717-1783)
[99] - Paolo Ruffini (1765-1822)
[100] - permutation
[101] - Hans Mathias Abel
[102] - Gjerstad
[103] - Niels Henrik Abel
[104] - Storting
[105] - Bernt Holmboe
[106] - Christoffer Hansteen
[107] - Treschow
[108] - Adrien-Marie Legendre (1752-1833)
[109]- Evariste Galois
[110] - Bourg-la-Reine
[111] - Bourg-l'Egalite
[112]- Orly Terquem
[113] - Saint-Simonians
[114]- EcolePreparatoire
[115] - EcoleNormale
[116] - Joseph Fourier
[117]- Simeon Poisson (1781-1840)
[118]- Sophie Germain (1831-1776) ریاضیدان زن فرانسوی.
[119] - Ernest Duchatelet
[120] - Carlos Infantozzi
[121]
- Stephanie-Felicie Poterin du
Motel
[122] - Eric Temple Bell
[123] - Louis Kollros
[124] - Pescheux D'Herbinville
[125] - Joseph-Louis Liouville
[126] - subgroup
[127] - normal subgroup of index p
[128] - alternating group
[129] - identity
[130] - Camille Jordan (1838-1922).
[131] - Representation theory.
[132] - Arthur Cayley (1821-1895).
[133] - trisecting the angle
[134] - duplicating the cube
[135] - squaring the circle
[136] - Pierre Laurent Wantzel (1814-1848)
[137] - Adhemard Jean Claude Barre de Saint-Venant (1797-1886)
[138] - Transcendental
[139] - Johann Lambert (1728-1777)
[140] - انتگرال هر تابع، تابعی است که مشتق آن برابر تابع اولیه میباشد.
[141] - Charles Hermite (1822-1901)
[142] - Henri Poincaré (1854-1912)
[143]
- Carl Louis Ferdinand von
Lindemann (1852-1939)
[144] - Felix Klein (1849-1925)
[145] - David Hilbert (1862-1943)
[146] - Johann Gustav Hermes (1846-1912)
[147] - John Horton Conway (1937- )
[148] - William Rowan Hamilton (1805-1865)
[149] - Eric Temple Bell (1883-1960)
[150] - Zerah Colburn
[151] - Hamiltonian systems
[152] - momentum
[153] - William Wordsworth (1770-1850)
[154] - Samuel Taylor Coleridge (1772-1834)
[155] - diffraction
[156] - Interference
[157] - characteristic function
[158] - Principle of Least Time
[159] - Snell's law of refraction
[160] - quaternions
[161] - Simon Stevin (1548-1620)
[162] - در عدد نویسی مدرن غربی از علامت (.)، که کوچک شده صفر است، برای ممیز اعشاری استفاده میکنند (مترجم).
[163] - imaginary
[164]- تفکر جنبی یا (lateral thinking)
عبارت است از روشهای حل مسئله از طریق راههای غیرمستقیم و خلاقانه. (مترجم)
[165] - complex plane
[166] - Johann Bernoulli (1667-1748)
[167] - Gottfried Leibniz (1646-1717)
[168] - Jean-Robert Argand (1768-1822)
[169] - Argand diagram
[170] - multiplicative invers
[171] - Peter Tait (1831-1901)
[172] - Benjamin Peirce (1809-1880)
[173] - Hermann Grassmann (1809-1877)
[174] - Josiah Willard Gibbs (1839-1903)
[175] - مراد کشف حساب دیفرانسیل و انتگرال در قرن هفدهم توسط نیوتون و لایبنیتس است. (مترجم)
[176] - این جمله کنایهای است به افکار و نقل قولهای ریاضیدان
آمریکایی اریک تمپل بل، که کتاب ”ریاضیدانان نامی“ او بسیار معروف است، ولی بسیاری
نیز محتوای آنرا از نظر تاریخی تائید نشده و اغراق آمیز میداند. این کتاب اولین
بار در سال 1348 توسط حسن صفاری به فارسی ترجمه، و توسط انتشارات امیرکبیر منتشر
شد. (مترجم)
[177] - field
[178] - division algebra
[179] - Adolf Hurwitz (1859-1919)
[180] - Marius Sophus Lie (1842-1899)
[181] - Julius Plucker
(1801-1868)
[182] - Jean-Victor Poncelet (1788-1867)
[183] - پروس نام قلمروی بود که در اوایل قرن بیستم منحل شد، و شامل بخشهایی از شرق آلمان و غرب لهستان میشد. (مترجم)
[184] - Leopold Kronecker (1823-1891)
[185] - Ernst Kummer (1810-1893)
[186] - Karl Weierstrass (1815-1897)
[187] - Felix Klein (1849-1825)
[188] - Camille Jordan (1838-1922)
[189] - Erlangen Program
[190] - شهری مرزی در شمال فرانسه. (مترجم)
[191] - continuous
[192] - Lie group
[194] - Lie algebra
[195] - commutator
[196] - Emmy Noether (1882-1935)
[197]
- Wilhelm Karl
Joseph Killing (1947-1923)
[198]
- Hermann von Helmholtz
(1821-1894)
[199] - classification
[200] - symplectic
[201] - root system
[202] - kaleidoscope
[203] - Élie Cartan (1869-1951)
[204] - octonions
[205] - Subtle Is the Lord by Abraham Pais.
[206] - Mathematical Principles of Natural Philosophy
[207] - James Clerk Maxwell (1831-1879)
[208] - Robert Hooke (1635-1703)
[209] - corpuscle
[210] - aether . در برخی کتابهای فارسی اِتر هم نوشته شده. (مترجم)
[211] - Terry Pratchett
[212] - Discworld
[213] - luminiferous aether
[214] - Christiaan Huygens (1629-1695)
[215] - Michael Faraday (1791-1867)
[216] - Sandemanians
[217] - Sir Humphry Davy (1778-1829)
[218] - Hans Christian Ørsted (1777-1851)
[219] - James Clerk Maxwell (1831-1879)
[220] - Heinrich Hertz (1857-1894)
[221] - Guglielmo Marconi (1874-1937)
[222] - Global Positioning System
[223] - Elektronische Fabrik J. Einstein und Co.
[224] - Immanuel Kant (1724-1804)
[225] - بر میتسوا (bar mitzvah) جشن تکلیفی است که برای پسران 13 ساله یهودی برگذار میشود (مترجم).
[226] - Adolf Hurwitz (1859-1919)
[227] - Hermann Minkowski (1864-1909)
[228] - Marcel Grossmann (1878-1936)
[229] - Mileva Maric (1878-1948)
[230] - Thorvald Thiele (1838-1910)
[231] - Louis Bachelier (1870-1946)
[232] - Marian Smoluchowski (1872-1917)
[233] - kinetic theory
[234] - Giordano Bruno
[235] - Albert Michelson (1852-1931)
[236] - Edward Morley (1938-1923)
[237] - invariant theory
[238] - Henri Poincare (1854-1912)
[239] - Hermann Minkowski (1864-1909)
[240] - Hendrik Lorentz (1853-1928)
[241] - general relativity
[242] - metric
[243] - triangle inequality
[244] - Doctor Who
[245] - Tardis
[246] - local
[247] - Riemannian manifold
[248] - equivalence principle
[249] - Lorentz-invariance
[250] - Gregorio Ricci-Curbastro (1853-1925)
[251] - Tullio Levi-Civita (1873-1941)
[252] - stress-energy tensor
[253] - Bianchi identities
[254] - perihelion
[255] - tensor
[256] - unified field theory
[257] - Philipp von Jolly (1809-1884)
[258] - Max Planck (1858-1947)
[259] - entropy
[260] - Otto Hahn (1879-1968)
[261] - Lise Meitner (1878-1968)
[262] - Blackbody radiation
[263] - ultraviolet catastrophe
[264] - Wilhelm Wien (1864-1928)
[265] - Niels Bohr (1885-1968)
[266] - Louis de Broglie (1892-1987)
[267] - wavicles
[268] - Erwin Schrödinger (1887-1961)
[269] - Franz Exner (1849-1926)
[270] - Friedrich Hasenöhrl (1874-1915)
[271] - Paul Dirac (1902-1984)
[272] - negentropy
[273] - Francis Crick (1916-2004)
[274] - James Watson (1928- )
[275] - superposition
[276] - decoherence
[277] - Werner Heisenberg (1901-1976)
[278] - Arnold Sommerfeld (1868-1951)
[279] - Max Born (1882-1970)
[280] - matrix
[281] - collapse
[282] - uncertainty principle
[283] - double cover
[284] - spinors
[285] - antimatter
[286] - Jenő Pál Wigner (1902-1995)
[287] - János (John) von Neumann (1903-1957)
[288] - group representation theory
[289] - Hermann Weyl (1885-1955)
[290] - spontaneous symmetry-breaking
[291] - Eugene Paul
[292] - سیاهچاله به نواحی از فضا-زمان گفته میشود که حتی نور هم نمیتواند از آن بگریزد، و بوسیله سقوط ستارگان سنگین تحت جاذبه خودشان بوجود میآیند.
[293] - Theory of Everything
[294] - Let there be light، عبارتی از انجیل:
آیه سوم از کتاب آفرینش است که به آغاز خلقت جهان و پیدایش نور اشاره دارد
(مترجم).
[295] - electroweak
[296] - توضیحات بیشتر در اینباره، در ادامه همین فصل خواهد آمد.
[297] - Isaac Asimov (1920-1992)
[298] - ارتباط ذهنی انسانها با یکدیگر (مترجم).
[299]- Königsberg
[300] - topology
[301] - Theodor Kaluza (1885-1954)
[302] - اکتوپلاسم (ectoplasm)
ماده فرضی است که در مدیومها (کسانی که احضار روح میکنند) وجود دارد، و ارواح برای
برقراری ارتباط و نشان دادن کارهای خود از آن ماده استفاده میکنند. (مترجم)
[303] - Edwin Abbott Abbott (1838-1926)
[304] - Flatland
[305] - multiverse
[306] - Oskar Klein (1894-1977)
[307] - gauge symmetries
[308] - supersymmetries
[309] - local symmetries
[310] - global symmetry
[311] - ((radioactive decay واپاشی رادیواکتیو عبارت است از خاصیتی که برخی عناصر دارا هستند و از خود ذرات و پرتو بیرون میدهند و نهایتاً به عنصر دیگری تبدیل میشوند.
[312] - اسپین به معنای چرخش است. ولی همانطور که در ادامه مطلب مشخص میشود،
با چرخش معمولی تفاوت دارد.
[313] - Enrico Fermi (1901-1954)
[314] - Satyendra Nath Bose (1894-1974)
[315] - fermions
[316] - bosons
[317] - Pauli exclusion principle
[318] - muon, tauon, lambda, sigma, xi, omega
[319] - pion, kaon, eta
[320] - quark
[321] - up, down, strange, charm, top, bottom
[322] - antiquark
[323] - quantum chromodynamics
[324] - gluons
[325] - weakons
[326] graviton
[327] - Chen Ning Yang (1922- )
[328] - Robert Mills (1927-1999)
[329] - Yang-Mills field
[330] - unitary transformation
[331] - GUT= Grand Unified Theory
[332] - decay
[333] - Tree of Life
[334] - Speciation
[335] - Watergate
[336] - Richard Nixon (1913-1994)
[337] - Bob Woodward (1943-)
[338] - Carl Bernstein (1944-)
[339] - (Deep Throat) نام یک فیلم مستهجن است، که مربوط به همان دوران بود و در زمان خود جنجال زیادی بپا کرد. این نام بر جنجالی بودن شخص خبرچین و موضوع واترگیت دلالت دارد. (مترجم)
[340] - Mark Felt (1913-2008)
[341] - Fields Medal
[342] - Edward Witten (1951-)
[343] - Louis Witten (1921-)
[344]
- topological quantum field
theories
[345] - Simon Donaldson (1957-)
[346] - دستگاههای مختصاتی که در آنها انجام عملیات حسابان میسر است.
[347] - knot theory
[348] - positive mass conjecture
[349] - Richard Schoen (1950-)
[350] - Shing-Tung Yau (1949-)
[351] - Supersymmetry
[352] - sparticle
[353] - selectron
[354] - squarks
[355] - photino
[356] - Marston Morse (1892-1977)
[357] - Sir Michael Atiyah (1929-)
[358] - strings
[359] - superstrings
[360] - world line
[361] - Feynman diagram
[362] - Yoichiro Nambu (1921-)
[363] - worldsheets
[364] - Gabriele Veneziano (1942-)
[365] - hadron
[366] - John Schwarz (1941-)
[367] - Joël Scherk (1946-1980)
[368] - graviton
[369] - Pierre Ramond (1943-)
[370] - André Neveu (1946-)
[371] - Michael Green (1946-)
[372] - anomalies
[373] - (charm)، به این عدد طعم یا (Flavour) ذره نیز میگویند.
[374] - torus
[375] - Philip Candelas
[376] - Gary Horowitz
[377] - Andrew Strominger
[378] - Calabi-Yau manifold
[379] - heterotic
[380] - noncommutative geometry
[381] - Alain Connes
[382] - noncommutative space
[383] - loop quantum gravity
[384] - Abhay Ashtekar (1949-)
[385] - grainy
[386] - Sundance Bilson-Thompson
[387] - braid
[388] - singularity
[389] - knots
[390] - localized waves
[391] - braid group
[392] - vacuum energy
[393] - fine-tuning
[394] - weak anthropic principle
[395] - strong anthropic principle
[396] - Raphael Bousso
[397] - Joseph Polchinski (1954-)
[398] - tunneling
[399] - Paul Steinhardt (1952-)
[400] - Niel Turok
[401] - Big Bang
[402] - Big Crunch
[403] - octonions
[404] - abstract algebra
[405] - John Baez (1961-)
[406] - John Graves
[407] - Octave
[408] - Arthur Cayley (1821–1895)
[409] - elliptic function
[410] - Fano plane
[411] - finite geometry
[412] - unit
[413] - surreal
[414] - norm
[415] - Degen
[416] - Cayley-Dickson
[417] - sedenions
[418] - law of small numbers
[419] - division algebras
[420] - normed division algebras
[421] - Adolf Hurwitz (1859-1919)
[422] - Max Zorn (1906-1993)
[423] - Godfrey Harold Hardy (1877-1947)
[424] - skew-Hermitian
[425] - orthogonal Lie algebras
[426] - unitary Lie algebras
[427] - symplectic Lie algebras
[428] - Elie Cartan (1869-1851)
[429] - identity transformation
[430] - Giotto
[431] - perspective
[432] - Filippo Brunelleschi
[433] - Piero della Francesca
[434] - Leonardo da Vinci
[435] - projection
[436] - projective geometry
[437] - finite projective geometry
[438] - Girard Desargues
[439] - Pascual Jordan (1902-1980)
[440] - Armand Borel (1923-2003)
[441] - Hans Freudenthal (1905-1990)
[442] - Jacques Tits (1930-)
[443] - Boris Rosenfeld
[444] - bioctonions
[445] - quateroctonions
[446] - octooctonions
[447] -vectors
[448] - spinors
[449]- John Keats (1795-1821) شاعر انگلیسی سبک رمانتیک. (مترجم)
[450] - Dirac’s delta function